
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

У разі, якщо
|
|
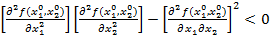 , (2.5)
, (2.5)
то в точці 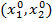 функція
функція 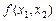 екстремуму не має.
екстремуму не має.
Якщо
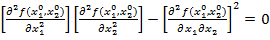 , (2.6)
, (2.6)
то питання про існування екстремуму залишається відкритим.
В загальному випадку перевірка достатніх умов здійснюється за допомогою складання матриці виду:
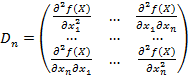 . (2.7)
. (2.7)
Стаціонарна точка 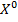 є точкою мінімуму функції
є точкою мінімуму функції 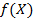 , якщо усі кутові мінори матриці
, якщо усі кутові мінори матриці 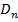 додатні, а саме
додатні, а саме 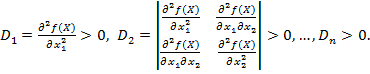
Стаціонарна точка 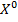 є точкою максимуму функції
є точкою максимуму функції 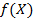 , якщо знаки кутових мінорів матриці
, якщо знаки кутових мінорів матриці 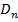 чергуються, при чому
чергуються, при чому 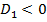 .
.
Якщо задача полягає у відшуканні локального чи глобального екстремуму деякої функції за умови, що на змінні такої функції накладаються додаткові обмеження, то маємо задачу пошуку умовного екстремуму функції. Термін «умовний» означає, що змінні задачі мають задовольняти деякі умови.
Розглянемо таку задачу для випадку двох змінних:
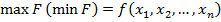 (2.8)
(2.8)
за умови
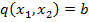 . (2.9)
. (2.9)
Найпростіший спосіб розв’язання задачі такого виду полягає в тому, що спочатку з обмеження (2.9) знаходять вираз однієї змінної через іншу. Приміром, визначають 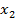 через
через 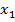 . Отриманий вираз виду
. Отриманий вираз виду 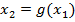 підставляють у функцію (2.8), що після цього стає функцією однієї змінної
підставляють у функцію (2.8), що після цього стає функцією однієї змінної 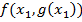 , і далі знаходять її безумовний екстремум.
, і далі знаходять її безумовний екстремум.
Якщо деяка точка 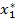 є точкою екстремуму функції
є точкою екстремуму функції 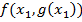 , то точка
, то точка 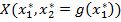 є точкою умовного екстремуму функції (2.8) за умови (2.9).
є точкою умовного екстремуму функції (2.8) за умови (2.9).
Однак не завжди вдається відшукати аналітичний вираз однієї змінної через іншу в умові (2.9). Часто це досить важко здійснити або неможливо. Також іноді складно узагальнити даний спосіб для функції n змінних, на які накладено m обмежень. Тому описана досить проста ідея зведення задачі відшукання умовного екстремуму функції кількох змінних до задачі на безумовний екстремум функції однієї змінної не може бути використана як основа універсального методу розв’язування задач на умовний екстремум. Цікавий метод розв’язування задач типу (2.8), (2.9) запропонував Лагранж.
3. Метод множників Лагранжа
Ідея методу множників Лагранжа полягає в заміні початкової задачі простішою. Для цього цільову функцію замінюють іншою, з більшою кількістю змінних, тобто такою, яка включає в себе умови, що подані як обмеження. Після такого перетворення дальше розв’язування задачі полягає в знаходженні екстремуму нової функції, на змінні якої не накладено ніяких обмежень. Тобто від початкової задачі пошуку умовного екстремуму переходимо до задачі відшукання безумовного екстремального значення іншої функції. Отже, завдяки такому перетворенню можливе застосування методів класичного знаходження екстремуму функції кількох змінних.
У попередньому параграфі наведена необхідна умова існування локального екстремуму неперервної та диференційованої функції двох змінних.
Узагальнення необхідної умови існування локального екстремуму функції n змінних має аналогічний вигляд. Отже, для розв’язування задачі необхідно знайти вирази частинних похідних нової цільової функції за кожною змінною і прирівняти їх до нуля. В результаті отримаємо систему рівнянь. Її розв’язок визначає так звані стаціонарні точки, серед яких є і шукані екстремальні значення функції.
Розглянемо метод множників Лагранжа для розв’язування задачі нелінійного програмування, що має вигляд:
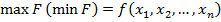 (3.1)
(3.1)
за умов:
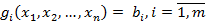 (3.2)
(3.2)
де функції 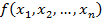 і
і  мають бути диференційовними.
мають бути диференційовними.
Задача (3.1), (3.2) полягає в знаходженні екстремуму функції 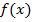 за умов виконання обмежень
за умов виконання обмежень 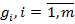 .
.
Переходимо до задачі пошуку безумовного екстремуму.
Замінюємо цільову функцію (3.1) на складнішу. Ця функція називається функцією Лагранжа і має такий вигляд:
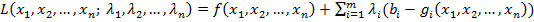 , (3.3)
, (3.3)
де 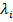 — деякі невідомі величини, що називаються множниками Лагранжа.
— деякі невідомі величини, що називаються множниками Лагранжа.
Знайдемо частинні похідні і прирівняємо їх до нуля:
 (3.4)
(3.4)
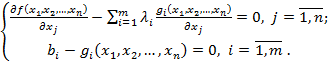 (3.5)
(3.5)
Друга група рівнянь системи (3.5) забезпечує виконання умов (3.2) початкової задачі нелінійного програмування.
Система (3.5), як правило, нелінійна.
Розв’язками її є 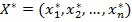 і
і 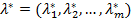 — стаціонарні точки. Оскільки, ці розв’язки отримані з необхідної умови екстремуму, то вони визначають максимум, мінімум задачі (3.1), (3.2) або можуть бути точками перегину (сідловими точками).
— стаціонарні точки. Оскільки, ці розв’язки отримані з необхідної умови екстремуму, то вони визначають максимум, мінімум задачі (3.1), (3.2) або можуть бути точками перегину (сідловими точками).
Для діагностування стаціонарних точок і визначення типу екстремуму необхідно перевірити виконання достатніх умов екстремуму, тобто дослідити в околі стаціонарних точок диференціали другого порядку (якщо для функцій 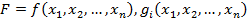 існують другі частинні похідні і вони неперервні).
існують другі частинні похідні і вони неперервні).
Узагальнення достатньої умови існування локального екстремуму для функції n змінних приводить до такого правила: за функцією Лагранжа виду (3.3) будується матриця Гессе, що має блочну структуру розмірністю 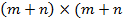 ):
):
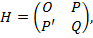 (3.6)
(3.6)
де  — матриця розмірністю
— матриця розмірністю 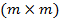 , що складається з нульових елементів,
, що складається з нульових елементів,
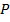 — матриця розмірністю
— матриця розмірністю 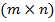 , елементи якої визначаються так:
, елементи якої визначаються так:
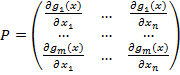 , (3.7)
, (3.7)
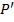 —
— 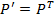 , транспонована матриця до
, транспонована матриця до 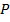 , розмірністю
, розмірністю 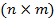 ,
,
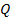 — матриця розмірністю
— матриця розмірністю 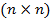 виду:
виду:
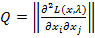 , де
, де 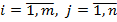 . (3.8)
. (3.8)
Розглянемо ознаки виду екстремуму розв’язку системи (3.5). Нехай стаціонарна точка має координати 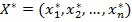 і
і 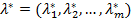 .
.
1. Точка 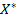 є точкою максимуму, якщо, починаючи з головного мінору порядку
є точкою максимуму, якщо, починаючи з головного мінору порядку 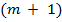 , наступні
, наступні 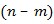 головних мінорів матриці
головних мінорів матриці  утворюють знакозмінний числовий ряд, знак першого члена якого визначається множником
утворюють знакозмінний числовий ряд, знак першого члена якого визначається множником 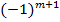 .
.
2. Точка 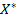 є точкою мінімуму, якщо, починаючи з головного мінору порядку
є точкою мінімуму, якщо, починаючи з головного мінору порядку 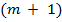 , знак наступних
, знак наступних 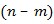 головних мінорів матриці
головних мінорів матриці  визначається множником
визначається множником 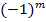 .
.
Розглянемо задачі, розв’язок яких знайдемо методом множників Лагранжа.
Приклад 3.1.
Знайти точку умовного екстремуму функції 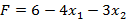 при обмеженні:
при обмеженні:
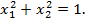
Розв’язання:
Складемо функцію Лагранжа 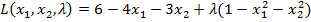 і продиференціюємо її по змінних
і продиференціюємо її по змінних 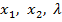 . Прирівнюючи отримані вирази до нуля, отримаємо наступну систему рівнянь:
. Прирівнюючи отримані вирази до нуля, отримаємо наступну систему рівнянь:

З першого і другого рівнянь випливає, що 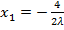 ,
, 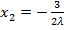 , тоді
, тоді
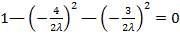 ;
;
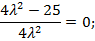
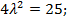
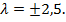
Отже, функція Лагранжа має дві стаціонарні точки:
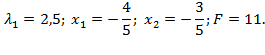
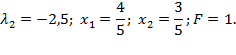
Побудуємо матрицю  , що складається з елементів
, що складається з елементів 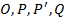 .
.
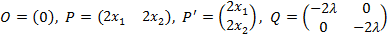 .
.
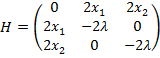 .
. 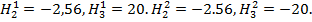
Отже  — точка, у якій функція досягає максимального значення
— точка, у якій функція досягає максимального значення 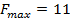 , а
, а 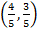 — точка, у якій функція досягає мінімального значення
— точка, у якій функція досягає мінімального значення 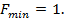
Date: 2015-07-24; view: 521; Нарушение авторских прав