Решение. В Excelлист с решением в режиме отображения формул для данной задачи выглядит следующим образом:

В Excelлист с решением в режиме отображения формул для данной задачи выглядит следующим образом:

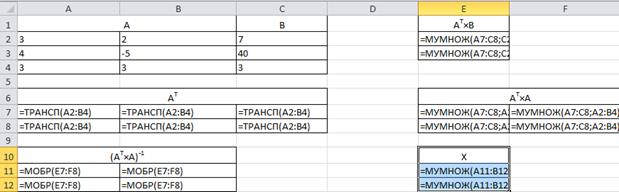
Результаты расчетов:

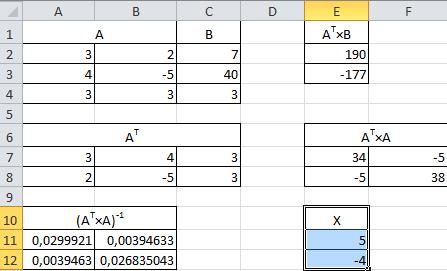
Искомый вектор Х расположен в диапазоне Е11:Е12.

При решении заданной системы линейных уравнений использовались следующие функции:

1. МОБР - возвращает обратную матрицу для матрицы, хранящейся в массиве.

Синтаксис: МОБР(массив).

Массив — числовой массив с равным количеством строк и столбцов.

После введения функции в левую верхнюю ячейку диапазона массива следует выделить массив, начиная с ячейки, содержащей формулу, нажать клавишу F2, а затем нажать клавиши CTRL+SHIFT+ENTER.

2. МУМНОЖ - возвращает произведение матриц (матрицы хранятся в массивах). Результатом является массив с таким же числом строк, как массив1 и с таким же числом столбцов, как массив2.

Синтаксис: МУМНОЖ(массив1;массив2).

Массив1, массив2 — перемножаемые массивы.

После введения функции в левую верхнюю ячейку диапазона массива следует выделить массив, начиная с ячейки, содержащей формулу, нажать клавишу F2, а затем нажать клавиши CTRL+SHIFT+ENTER.

3. ТРАНСП – преобразует вертикальный набор ячеек в горизонтальный, или наоборот. В результате использования этой функции появляется массив с числом строк, равным числу столбцов исходного массива, и числом столбцов, равным числу строк начального массива.

Заключение

В курсовой работе описаны некоторые классические ([4],[7]) методы решения систем линейных уравнений. Описан также метод наименьших квадратов и решение системы с прямоугольной матрицей, в которой число уравнений больше, чем число неизвестных. Решение этой системы также свелось к решению методом Гаусса системы с квадратной матрицей, получаемой из исходной системы умножением обеих частей на транспонированную матрицу.

Следует отметить (см. [2], [3], [4], [6], [7]), что в современных научных вычислениях в основном фигурируют методы решения больших, т.е. с размерностью более 1000, систем линейных алгебраических уравнений. В указанных книгах описаны существенно более изощренные методы решения алгебраических систем, для реализации которых на Excel’е требуется написание на языке Visual Basic новых макросов. Но, так как для решения больших систем Excel не пригоден в связи с низкой производительностью, то реализация этих методов в Excel не имеет смысла.

Список литературы

[1] Гельман В.Я. Решение математических задач средствами Excel.—Москва-

Санкт-Петербург: Питер,2003.

[2] Каханер Д. Моулер К., Нэш С. Численные методы и программное

обеспечение.—М.: Мир, 1998.

[3] Кормен Т., Лейзерсон Ч., Ривест Р. АЛГОРИТМЫ (построение и анализ). —

М.: МЦНМО, 2000.

[4] Райс Дж. Матричные вычисления и математическое обеспечение.— М.: Мир,

1984.

[5] Васильев А.Н. Научные вычисления в Microsoft Excel.— Москва-Киев: Диа-

лектика, 2004.

[6] Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических

вычислений. — М.:Мир, 1980.

[7] Press W.H., Teukolsky S.A., Flannery B.P. Numerical Recipes in C.— Cambridge

University Press, 1991.

Содержание

Введение. 2

1. Метод Гаусса и одно из его приложений в экономике (задача о рационе). 3

1.1. Простейшая задача о рационе. 3

1.2. Метод Гаусса. 3

1.3. Метод Гаусса в Excel. 5

2. Модель Леонтьева межотраслевого баланса. 7

3. Метод наименьших квадратов (МНК). 13

Date: 2015-07-24; view: 330; Нарушение авторских прав