Краткая сводка теоретических сведений, необходимых для выполнения задания 1

Для графического отделения F1(x) и F2(x), а потом на оси Х отмечаются отрезки, локализирующие абсциссы точек пересечения этих графиков.

Пример:

Для графического отделения корней уравнения sin2x-ln=0 преобразуем его к равносильному уравнению sin2x=lnx и отдельно посмотрим графики функции sin2x и lnx

Для графика вполне очевидно, что уравнение имеет единственный корень и этот корень находится на отрезке [1;1.5].

При решении задачи об отделении корней бывают полезными следующие очевидные положения:

ГРАФИК

1.Если непрерывная на отрезке [а;b] функция F(x) принимает на его концах значение разных знаков, то уравнение имеет на этом отрезке по меньшей мере один корень.

2. Если функция F(x) к тому же монотонна, то корень на отрезке [a,b] единственный.

Вычислим для проверки значение функции: F(x)=sin 2x-lnx на концах отрезка[1;1,5]: F(1)=0,909298; F(1,5)=-0,264344. Как видно, корень на отрезке [1;1,5] действительно имеется.

Рассмотренный прием позволяет при желании сузить отрезок, полученный графическим способом. Так, в нашем примере имеем F(1,3)=0,253138>0, так что отрезком, на котором находится корень, можно считать [1,3;1,5].

В простейших случаях графическое отделение корней можно осуществить в ручную, однако более сложных случаях для исследования вопроса о наличии и количестве корней уравнения на заданном отрезке целесообразнее воспользоваться инструментальным пакетом или составить программу для компьютера на языке программирования. Рассмотрим коротко суть идеи для применения указанных подходов.

Пусть имеется уравнение F(x)=0, причем известно что все интересующие вычислителя корни находятся на отрезке [A,B], на котором функция F(x) определена, непрерывной и F(A) F(B)<0. Требуется определить корни уравнения, т.е. указать все отрезки [a;b] 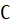[A;B], содержащие по одному корню.

Будем вычислять значения F(x), начиная с точки х=А, двигаясь вправо с некоторым шагом h.

Как только обнажится пара соседних значений F(x), имеющих разные знаки, и функция F(x) монотонна на этом отрезке, так соответствующие значения аргумента х предыдущее и следующие можно считать концами отрезка, содержащего корень.

Решение:

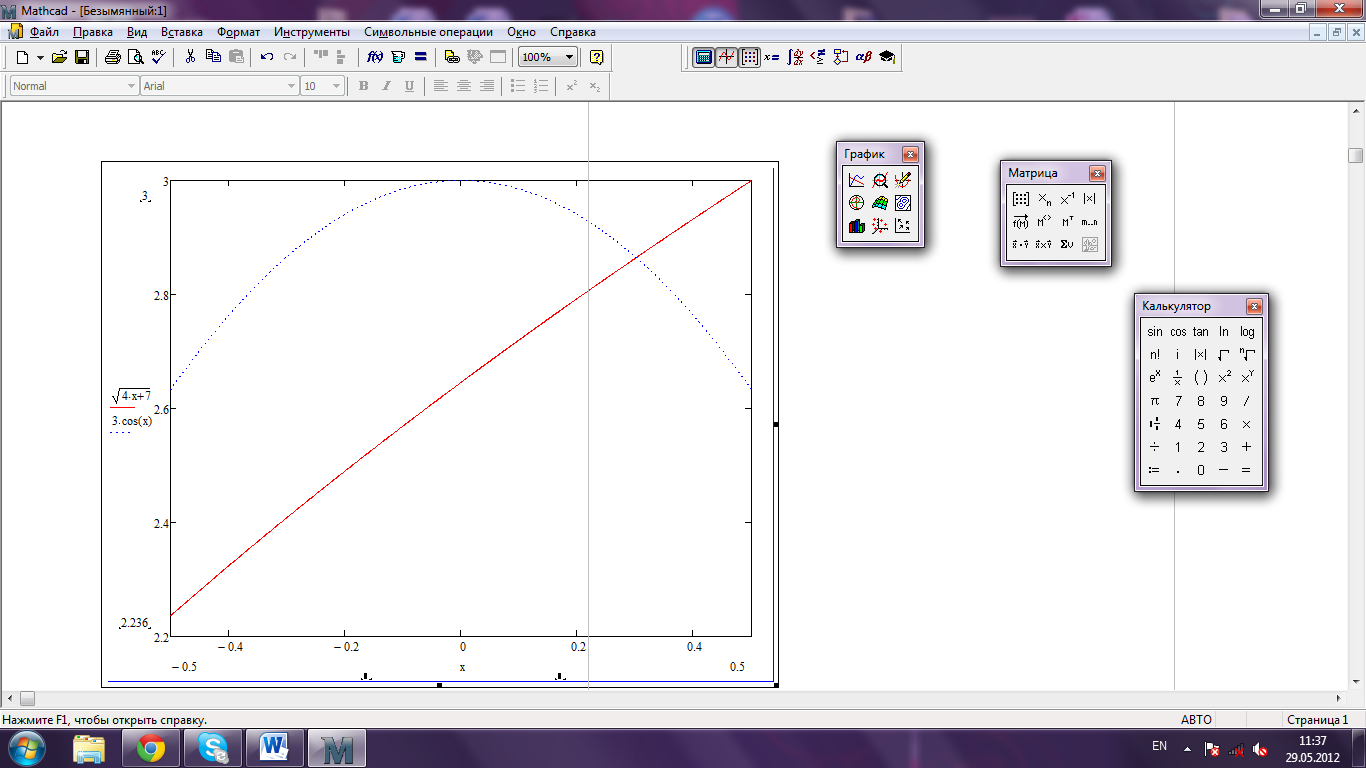
При выполнении задания отделение корней заданного уравнения выполнялся с помощью схематического графика на бумаге. Во многих случаях задачу графического отделения корня можно упростить, заменив исходное уравнение вида F(x)=0 равносильным ему уравнением.

Пользуясь программой маткад получили данное уравнение где значение приблеженно равно 2,5.

Date: 2015-07-24; view: 413; Нарушение авторских прав