
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Диамагнетизм
|
|
Рассмотрим магнитные свойства атома, воспользовавшись моделью Бора: одноэлектронный атом – это ядро и вращающийся вокруг него по орбите электрон. Такой электрон можно уподобить круговому току с магнитным моментом, называемым орбитальным:
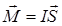 ,
, 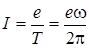 , (4.42)
, (4.42)
где Т – период вращения, 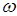 - круговая частота. Тогда, зная, что
- круговая частота. Тогда, зная, что 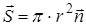 , где
, где 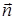 - нормаль к плоскости витка,
- нормаль к плоскости витка, 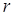 - радиус витка, получаем:
- радиус витка, получаем:
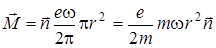 . (4.43)
. (4.43)
Механический момент электрона на орбите:
 . (4.44)
. (4.44)
Из (4.43) и (4.44) следует магнитомеханическое отношение для орбитальных моментов 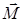 и
и 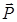 :
:
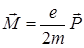 . (4.45)
. (4.45)
Поскольку заряд электрона отрицателен, векторы 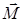 ,
, 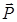 антипараллельны.
антипараллельны.
Для изучения поведения одноэлектронного атома в магнитном поле учтем, что при 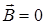 на электрон действуют две силы (кулоновская и центростремительная); уравнение движения запишем так:
на электрон действуют две силы (кулоновская и центростремительная); уравнение движения запишем так:  ;
;
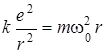 , (4.46)
, (4.46)
где 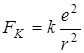 ,
, 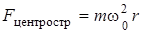 .
.
Поместим атом в магнитное поле 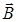 так, чтобы вектор
так, чтобы вектор 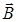 был перпендикулярен плоскости орбиты. Возникает сила Лоренца, изменяющая скорость движения электрона
был перпендикулярен плоскости орбиты. Возникает сила Лоренца, изменяющая скорость движения электрона 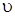 , но не изменяющая радиус орбиты, ее величина:
, но не изменяющая радиус орбиты, ее величина:
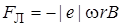 ,
,
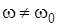 . Уравнение движения электрона при
. Уравнение движения электрона при 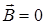 приобретает следующий вид:
приобретает следующий вид:
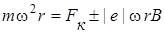 ; (4.47)
; (4.47)
знак “±” выбирается в соответствии с относительной ориентацией 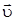 и
и 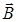 (или
(или 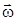 и
и 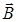 ) (см.рис.4.9).Учтем (4.46), тогда (4.47) перепишется следующим образом:
) (см.рис.4.9).Учтем (4.46), тогда (4.47) перепишется следующим образом:
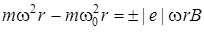 . (4.48)
. (4.48)
Так как 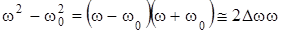 , при
, при 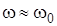 , то
, то
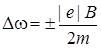 . (4.49)
. (4.49)
Обозначим:
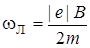 . (4.50)
. (4.50)
Тогда из (4.49) следует, что в магнитном поле частота вращения электрона изменяется на дополнительную величину 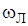 , называемую ларморовой частотой:
, называемую ларморовой частотой:
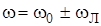 . (4.51)
. (4.51)
Найдем направление вектора 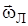 . Так как
. Так как 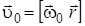 , то две ориентации
, то две ориентации 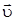 отвечают двум ориентациям
отвечают двум ориентациям 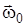 (см. рис.4.9):
(см. рис.4.9): 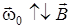 и
и 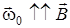 . При этом
. При этом 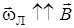 всегда. Таким образом:
всегда. Таким образом:
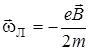 . (4.52)
. (4.52)
Это все справедливо для случая, когда вектор 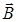 перпендикулярен плоскости орбиты. Если же вектор
перпендикулярен плоскости орбиты. Если же вектор 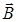 составляет с плоскостью орбиты угол, отличный от
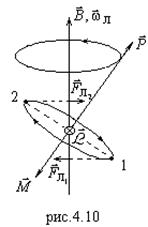
составляет с плоскостью орбиты угол, отличный от 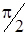 (рис.4.10), то атом можно рассматривать как гироскоп с уравнением движения:
(рис.4.10), то атом можно рассматривать как гироскоп с уравнением движения:

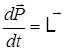 ,
,
где 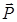 - механический момент,
- механический момент,  - момент внешних сил (лоренцевых
- момент внешних сил (лоренцевых 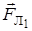 и
и 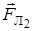 ), см. на рис.4.10. Так же, как для гироскопа, в результате будет происходить прецессия атома в магнитном поле с частотой Лармора.
), см. на рис.4.10. Так же, как для гироскопа, в результате будет происходить прецессия атома в магнитном поле с частотой Лармора.
В §3.1 было получено, что: 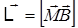 , тогда с учетом (4.45):
, тогда с учетом (4.45):
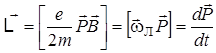 . (4.53)
. (4.53)
Выражение (4.53) сравним с 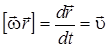 . Значит, атом как целое прецессирует вокруг
. Значит, атом как целое прецессирует вокруг 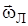 (или
(или 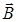 ) с частотой ларморовой прецессии (рис.4.10).
) с частотой ларморовой прецессии (рис.4.10).
 За счет чего изменяется частота вращения электрона в магнитном поле? За счет явления электромагнитной индукции, так как при возникновении магнитного поля появляется индукционный ток, т.е. изменяется скорость движения электрона в атоме.
За счет чего изменяется частота вращения электрона в магнитном поле? За счет явления электромагнитной индукции, так как при возникновении магнитного поля появляется индукционный ток, т.е. изменяется скорость движения электрона в атоме.
С возникшей добавочной частотой связан магнитный момент. По (4.43):
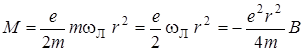 . (4.54)
. (4.54)
Видно, что:
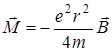 , (4.55)
, (4.55)
т.е. векторы 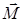 и
и 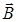 антипараллельны, таким образом
антипараллельны, таким образом 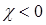 . Чтобы оценить величину восприимчивости единицы объема магнетика, нужно учесть:
. Чтобы оценить величину восприимчивости единицы объема магнетика, нужно учесть:
а) количество электронов в атоме (Z – атомный номер в периодической таблице Менделеева);
б) число атомов в единице объема - N.
в) отличие формы орбиты от круговой (усреднить r2);
c) возможность ориентации 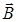 неперпендикулярно плоскости витка (запишем
неперпендикулярно плоскости витка (запишем 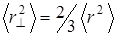 ). Окончательно для намагниченности получаем:
). Окончательно для намагниченности получаем:
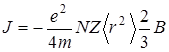 . (4.56)
. (4.56)
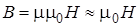 , поскольку
, поскольку 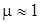 . Тогда:
. Тогда:
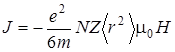 . (4.57)
. (4.57)
Таким образом, из (4.19) и (4.57) следует, что:
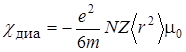 , (4.58)
, (4.58)
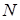 - число атомов в единице объема;
- число атомов в единице объема; 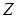 - атомный номер (число электронов);
- атомный номер (число электронов); 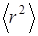 - среднее значение квадрата радиуса боровской орбиты;
- среднее значение квадрата радиуса боровской орбиты; 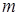 - масса электрона.
- масса электрона.
Из формулы (4.58) видно, что 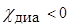 и
и 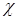 не является функцией температуры. Если подставить все входящие в формулу величины, то получаем:
не является функцией температуры. Если подставить все входящие в формулу величины, то получаем:
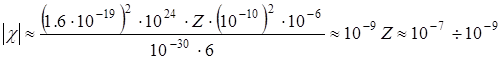 .
.
Так, для He 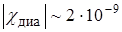 ; для Ar
; для Ar 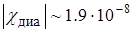 ; для Xe
; для Xe 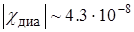 .
.
Явление диамагнетизма универсально и присуще всем элементам. Чистый диамагнетизм должен наблюдаться у элементов с нулевым орбитальным моментом, т.е. у элементов с заполненными электронными оболочками. К таким относятся инертные газы, ионы щелочных металлов и галогенов.
Date: 2015-07-24; view: 362; Нарушение авторских прав