
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Абстрактный синтез дискретного автомата
|
|
ВВЕДЕНИЕ
Современные приборы и устройства сервиса представляют собой сложные технические системы, реализованные на базе средств вычислительной техники. Цифровые устройства и микропроцессоры являются важнейшей составной частью различных объектов бытовой техники: радиоэлектронной аппаратуры, стиральных и посудомоечных машин, холодильников и климат-систем, изделий оргтехники и других устройств.
Такой широкий диапазон применения цифровых устройств определяется их высокими техническими параметрами и технико-экономическими показателями. В частности - это низкое энергопотребление, высокое быстродействие, высокая надежность и помехозащищенность, возможность реализации алгоритмов управления и обработки сигналов любой сложности, малые габариты, технологичность и низкая стоимость [1].
Управляющие автоматы реализуются в виде "гибкой" или программируемой логики, на основе микропроцессоров, а также в виде "жесткой логики" - на основе последовательностных цифровых устройств. Математическими моделями, используемыми при анализе и синтезе последовательностных устройств. В последнее время интерес к конечным автоматам возрос, что связано с развитием интегральной программируемой электроникии др. В основе синтеза таких устройств лежат методы абстрактного (логического) и структурного синтеза конечных автоматов. Это обстоятельство делает необходимым приобретения знаний и навыков применения этих методов для анализа и синтеза цифровых устройств управления объектами и устройствами [2].
абстрактный синтез дискретного автомата
Рассмотрим содержание и особенности определенных этапов синтеза на примере
Пусть требуется синтезировать асинхронный автомат Мура начальное описание, которого представлено вход-выходной последовательностью и таблицей соответствия:
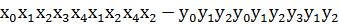 .
.
Определяем мощность входного и выходного множества Мх=5 Му=4.Строим первичную таблицу переходов-выходов автомата Мура, как показано в соответствии с таблицей 1.
Таблица 1.1 Первичная таблица переходов-выходов автомата Мура
| х | Состояния S и выходные сигналы Y | |||||||||
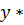
| 
| 
| 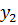
| 
| 
| 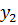
| 
| 
| 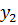
| |
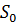
| 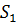
| 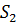
| 
| 
| 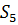
| 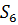
| 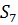
| 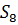
| 
| |
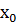
| 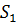
| 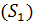
| - | - | - | - | - | - | - | 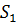
|
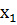
| - | 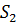
| 
| - | - | 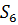
| 
| - | - | - |

| - | - | 
| 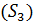
| - | - | 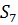
| 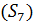
| 
| 
|
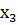
| - | - | - | 
| 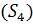
| - | - | - | - | - |
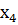
| - | - | - | - | 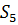
| 
| - | 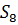
| 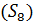
| - |
Задача минимизации автомата сводится возможности максимального уменьшения числа внутренних состояний без изменения закона их функционирования.
Решение этой задачи выполним методом Ауфенкампа и Хона основанного на понятии эквивалентных состояний.
Эквивалентным состоянием называется sn и sm такие состояния которым во-первых соответствуют одинаковые входные сигналы y(t) а во вторых переход из состояний sn и smпод воздействием любого символа приводит к одному и тому же эквивалентному состоянию[3].
Алгоритм минимизации:
1. Методом последовательного разбиения выделяем все попарно эквивалентные состояния.
2. Объединяем эквивалентные состояния в одиночные классы у1 у2и выделяем в каждом классе по одному состоянию для выполнения последующих этапов при разбиении на классы пустые клетки во внимание не принимаются.
3. Строим вторичную таблицу переходов-выходов в которой каждый класс состояний представляем только одним эквивалентным состоянием.
Первичный граф переходов-выходов автомата Мура представлен в соответствии с рисунком 1.
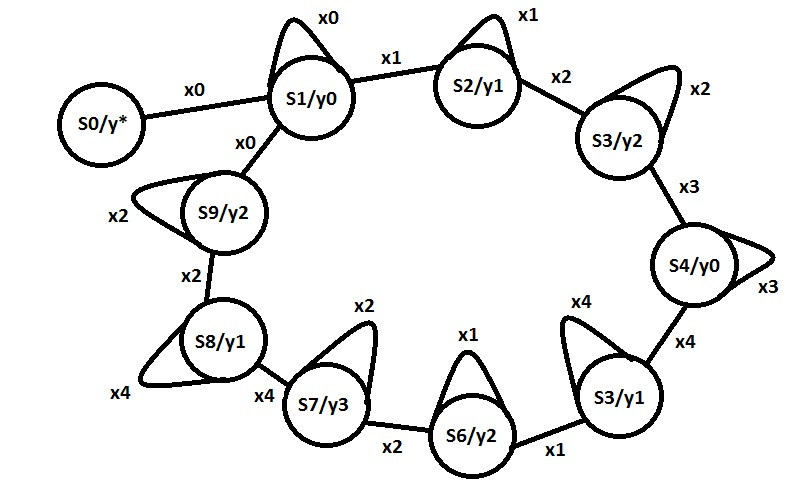
Рисунок 1 - Первичный граф переходов-выходов автомата Мура
Первое разбиение состояний на классы выполняем по выходным сигналам как показано в таблице 2.Анализ показывает что в классе у1 состояние s1 не является эквивалентным основным состоянием этого класса так как при поступлении сигнала х1 автомат переходит из состояния s1 в класс состояний у2 в отличии от других состояний класса переводящих автомат под действием сигнала х1 в состояния класса у1[4].
Таблица 2 - Разбиение на классы автомата Мура
| х | Состояния S и выходные сигналы Y | |||||||||

| 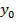
| 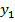
| 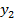
| 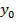
| 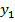
| 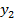
| 
| 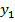
| 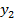
| |

| 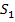
| 
| 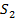
| 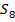
| 
| 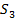
| 
| 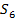
| 
| |
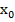
| 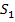
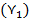
| 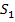
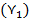
| - | - | - | - | - | 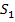
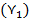
| - | - |

| - | 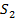

| - | 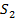

| - | 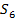
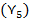
| - | - | 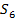
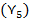
| - |
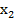
| - | - | - | 

| 

| - | 

| 

| 

| 

|
| - | - | 

| - | - | - | 
| - | - | - |

| - | - | 

| - | 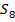

| 

| - | - | - | 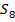

|
| Кл. | 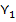
| 
| 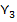
| 
| 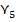
| 
|
Таблица 3 - Переходы-выходы автомата Мура
| x | Состояния Г и выходные сигналы Y | |||||

| 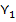
| 
| 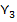
| 
| 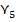
| |
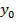
| 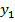
| 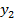
| 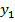
| 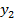
| 
| |
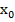
| 
| - | 
| - | - | - |

| 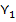
| 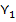
| - | 
| 
| - |
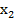
| - | 
| 
| - | 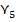
| 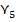
|
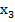
| 
| - | 
| - | - | - |

| 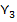
| 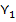
| - | 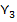
| - | 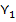
|
Таблица 4 - Первичная таблица возбуждения
| x | Y0 | Y1 | Y2 | Y2 | Y1 | Y2 | Y3 | Y3 | ||||||||||||||||||||||||
| d1 | d0 | d1 | d0 | d1 | d0 | d1 | d0 | d1 | d0 | d1 | d0 | d1 | d0 | d1 | d0 | |||||||||||||||||
| y0 | y1 | y2 | y*2 | y3 | y4 | y5 | y*5 | |||||||||||||||||||||||||
| q3 | q2 | q1 | q0 | q3 | q2 | q1 | q0 | q3 | q2 | q1 | q0 | q3 | q2 | q1 | q0 | q3 | q2 | q1 | q0 | q3 | q2 | q1 | q0 | q3 | q2 | q1 | q0 | q3 | q2 | q1 | q0 | |
| a2 | a1 | a0 | ||||||||||||||||||||||||||||||||
| - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |||||||||||
| - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |||||||||||||||||||
| - | - | - | - | - | - | - | - | - | - | - | - | |||||||||||||||||||||||
| - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |||||||||||
| - | - | - | - | - | - | - | - | - | - | - | - |
Таблица 5 - Вторичная таблица возбуждения
| x | Y0 | Y1 | Y2 | Y2* | ||||||||||||||||||||||||||||||
| d1 | d0 | d1 | d0 | d1 | d0 | d1 | d0 | |||||||||||||||||||||||||||
| y0 | y1 | y2 | y*2 | |||||||||||||||||||||||||||||||
| q3 | q2 | q1 | q0 | q3 | q2 | q1 | q0 | q3 | q2 | q1 | q0 | q3 | q2 | q1 | q0 | |||||||||||||||||||
| a2 | a1 | a0 | R3 | S3 | R2 | S2 | R1 | S1 | R0 | S0 | R3 | S3 | R2 | S2 | R1 | S1 | R0 | S0 | R3 | S3 | R2 | S2 | R1 | S1 | R0 | S0 | R3 | S3 | R2 | S2 | R1 | S1 | R0 | S0 |
| - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |||||||||||||||||||
| - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |||||||||||||||||||
| - | - | - | - | - | - | - | ||||||||||||||||||||||||||||
| - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |||||||||||||||||||
| - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
Продолжение таблицы 5
| x | Y1 | Y2 | Y3 | Y3* | ||||||||||||||||||||||||||||||
| d1 | d0 | d1 | d0 | d1 | d0 | d1 | d0 | |||||||||||||||||||||||||||
| y3 | y4 | y5 | y*5 | |||||||||||||||||||||||||||||||
| q3 | q2 | q1 | q0 | q3 | q2 | q1 | q0 | q3 | q2 | q1 | q0 | q3 | q2 | q1 | q0 | |||||||||||||||||||
| a2 | a1 | a0 | R3 | S3 | R2 | S2 | R1 | S1 | R0 | S0 | R3 | S3 | R2 | S2 | R1 | S1 | R0 | S0 | R3 | S3 | R2 | S2 | R1 | S1 | R0 | S0 | R3 | S3 | R2 | S2 | R1 | S1 | R0 | S0 |
| - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |||
| - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |||||||||||||||||||
| - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |||||||||||||||||||
| - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |||
| - | - | - | - | - | - | - | - |
Date: 2015-07-22; view: 493; Нарушение авторских прав