
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Давление металла на валки и момент прокатки
|
|
Следующей задачей, с которой приходится сталкиваться инженеру – технологу, является задача определения силы, действующей на валок при прокатке и момента прокатки.
Рассмотрение этой задачи ограничим случаем плоской деформации, которая реализуется, например, при прокатке листов, слябов и ленты.
Анализ проведем в соответствии с “ инженерным методом “ или иначе методом тонких сечений.
Согласно этому методу рассмотрим равновесие элемента полосы, мысленно вырезанного в зоне очага деформации (на рисунке показан элемент в зоне отставания) так, что высота элемента конечна и равна h, а длина dx, бесконечна мала.
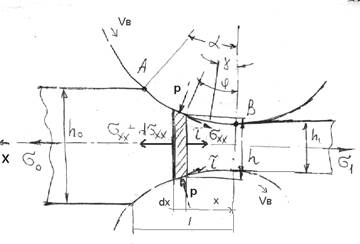
Составим условие равновесия выделенного элемента (сумма проекций всех сил, действующих на элемент, равна нулю)
 ,
,
где 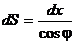 - длина дуги элемента.
- длина дуги элемента.
Пренебрегая бесконечно малыми второго порядка, получим
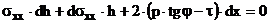
Если иметь в виду, что
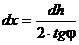 ,
,
то последнее дифференциальное уравнение можно переписать так
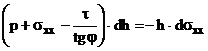 (2,15)
(2,15)
Инженерный метод рассматривает приближенное дифференциальное уравнение равновесия, в частности (2.15), совместно с условием пластичности.
Приближенное условие пластичности для плоского деформированного состояния имеет вид.
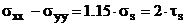
В данном случае имеем
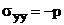
Тогда условие пластичности запишется
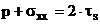 (2.16)
(2.16)
Совместное рассмотрение уравнений (2.15) и (2.16) значительно упрощается практически без ущерба для точности, если принять в пределах зоны отставания
 ,
,
а во всем очаге деформации считать, что
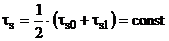
Здесь 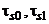 - предел текучести материала до и после прокатки.
- предел текучести материала до и после прокатки.
Тогда, имея в виду эти обстоятельства, из уравнений (2.15) и (2.16) получим
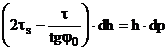 (2.17)
(2.17)
Для интегрирования уравнения (2.17) необходимо использовать какой – либо закон трения. Для простоты примем, что трение подчиняется условию

Тогда интеграл уравнения (2.17) будет
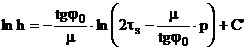
или
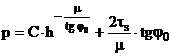 (2.18)
(2.18)
Используем граничные условия:
при 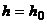
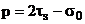
Тогда, исключая С из формулы (2.18), получим
 (2.19)
(2.19)
Обратимся к зоне опережения.
Если рассмотреть равновесие соответствующего элемента в этой зоне совместно с условием пластичности, то получим дифференциальное уравнение, аналогичное уравнению (2.17) (силы трения будут иметь иное направление, чем в зоне отставания)
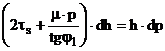
Здесь обозначено и принято
 .
.
Интегрирование этого дифференциального уравнения с учетом граничного условия
при 
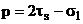
дает следующую формулу удельного давления для зоны опережения
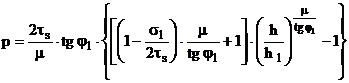 (2.20)
(2.20)
Согласно уравнениям (2.19) и (2.20) следует, что нормальное напряжение имеет минимум в точках А и В (см. рис.) и повышается по направлению к нейтральному сечению.
Максимум давления расположен вблизи нейтрального сечения.
При анализе найденного закона распределения р по дуге захвата можно видеть, что он зависит от многих факторов:
коэффициента внешнего трения, высоты прокатываемой полосы, обжатия диаметра валков и, наконец, натяжения прокатываемой полосы при её входе в валки 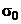 и выходе из них
и выходе из них 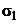 .
.
Располагая эпюрами удельных давлений р и касательных напряжений 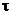 , можно путем интегрирования найти общее давление на валок
, можно путем интегрирования найти общее давление на валок
 (2.21)
(2.21)
и момент прокатки, который приложен к одному валку
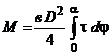 (2.22)
(2.22)
Часто давление на валок и крутящий момент определяют по приближенным формулам
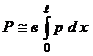 ;
; 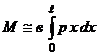 (2.23)
(2.23)
Расчет силовых параметров прокатки требует назначения 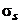 или
или 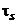 . Правильный выбор сопротивления деформации является необходимым условием надежности расчетных данных.
. Правильный выбор сопротивления деформации является необходимым условием надежности расчетных данных.
При холодной прокатке 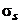 определяется только в зависимости от степени деформации. Степень деформации после прокатки приближенно можно оценить так
определяется только в зависимости от степени деформации. Степень деформации после прокатки приближенно можно оценить так

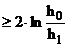
По кривым упрочнения можно найти 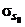 и
и  - сопротивление деформации в начале и в конце очага деформации – и тогда среднее его значение в очаге деформации будет
- сопротивление деформации в начале и в конце очага деформации – и тогда среднее его значение в очаге деформации будет
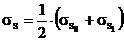
При горячей деформации необходимо для выбора 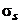 правильно оценить среднюю для очага деформации степень деформации
правильно оценить среднюю для очага деформации степень деформации  ср и скорость деформации Hср.
ср и скорость деформации Hср.
Например, это можно сделать так:
средняя степень деформации в очаге будет (между нулем и  =
= 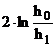 )
)
 ср
ср 
тогда
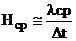
Здесь 
Далее для  ср и Hср по кривым упрочнения для данного материала и температуры определяется
ср и Hср по кривым упрочнения для данного материала и температуры определяется 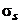 .
.
| <== предыдущая | | | следующая ==> |
| Да будет свет | | | Предназначение, задачи и объекты действий подразделений дальней авиации (ДА) |
Date: 2015-07-23; view: 870; Нарушение авторских прав