
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

В задачах сделать расшифровку (объяснение) основных терминов, понятий, определений
|
|
Вариант 4
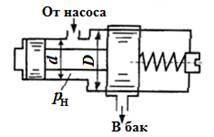 Задача 2с.4. Определить величину предварительного поджатия пружины дифференциального предохранительного клапана, обеспечивающую начало открытия клапана при давлении р н. Диаметры клапана D, d; жесткость пружины k. Давление справа от большого и слева от малого поршней – атмосферное.
Задача 2с.4. Определить величину предварительного поджатия пружины дифференциального предохранительного клапана, обеспечивающую начало открытия клапана при давлении р н. Диаметры клапана D, d; жесткость пружины k. Давление справа от большого и слева от малого поршней – атмосферное.
| Величина | Варианты | |||||||||
| р н, МПа | 0,8 | 1,5 | 1,2 | 1,8 | 2,2 | 2,4 | 2,6 | |||
| D, мм | ||||||||||
| d, мм | ||||||||||
| k, Н/мм |
Пример решения задачи.
Последовательность работы дифференциального предохранительного клапана.
Назначение клапана состоит в том, чтобы при значении давления жидкости большем значения Pн, золотник, перемещаясь вправо, открывал сливное окно и тем самым обеспечивал безаварийную работу либо самого насоса либо устройства, в которое нагнетается насосом жидкость. Из этого требования следует, что пружина клапана должна создавать силу, действующую на золотник справа налево, равную силе, создаваемой жидкостью при давлении Pн. Предполагается, что давление Pн – это абсолютное давление жидкости. Тогда, сумма всех действующих на золотник сил, создаваемых атмосферным давлением, равна нулю и сформулированное требование может быть записано уравнением
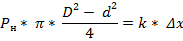
В этом уравнении 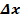 – предварительное поджатие пружины клапана.
– предварительное поджатие пружины клапана.
Ответы
| Величина | Варианты | |||||||||
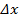 , мм , мм
| 26,4 |
|
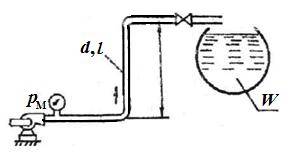 Задача 3с.5. По трубопроводу диаметром d насос перекачивает жидкость Ж на высоту Н. Коэффициент сопротивления вентиля ζ = 8. За какое время насос наполнит резервуар емкостью W, если манометр, установленный на выходе из насоса, показывает избыточное давление р м. Сопротивлением трубопровода пренебречь.
Задача 3с.5. По трубопроводу диаметром d насос перекачивает жидкость Ж на высоту Н. Коэффициент сопротивления вентиля ζ = 8. За какое время насос наполнит резервуар емкостью W, если манометр, установленный на выходе из насоса, показывает избыточное давление р м. Сопротивлением трубопровода пренебречь.| Величина | Варианты | ||||||||||||||||||
| Ж | В | Б | К | ДТ | Н | Б | К | В | Б | Н | |||||||||
| Плотность, кг/м3 | |||||||||||||||||||
| d, мм | |||||||||||||||||||
| Н, м | |||||||||||||||||||
| W, м3 | |||||||||||||||||||
| p м, кПа | |||||||||||||||||||
Обозначения: Б – бензин, В – вода, К – керосин, ДТ –дизельное топливо,
Н – нефть.
Пример решения задачи.
Из постановки задачи следует: весь полный напор расходуется на подъём жидкости на высоту H, на преодоление потерь давления в вентиле и на потери, вызванные внезапным расширением потока на выходе из трубопровода. Докажем это, используя уравнение Бернулли. Примем начало отсчёта высот столба жидкости от оси выходного патрубка насоса.

В этом уравнении α - коэффициент Кориолиса, который учитывает неравномерность эпюры скоростей в сечении патрубка (см. задачу 3с.1).
В соответствии с условием задачи второе слагаемое в правой части уравнения учитывает потери напора при внезапном расширении потока на выходе из трубопровода (теряется один скоростной напор).
Из этого уравнения следует
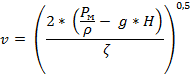
Расход жидкости определим по соотношению
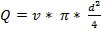 ,
,
а время наполнения резервуара из уравнения
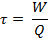
Ответы.
| Величина | Варианты | |||||||||
| v, м/с | 6,54 | |||||||||
| Q, м3/c | 0,0329 | |||||||||
| τ, c |
Задача 4с.1. Определить скорость движения поршня диаметром D, который под действием силы F вытесняет жидкость с плотностью ρ из правой полости гидроцилиндра через насадок с диаметром d и коэффициентом расхода μ.
| Величина | Варианты | |||||||||
| F, кН | ||||||||||
| D, мм | ||||||||||
| d, мм | ||||||||||
| µ | 0,82 | 0,62 | 0,72 | 0,65 | 0,7 | 0,62 | 0,7 | 0,65 | 0,82 | |
| ρ, кг/м3 |
Пример решения задачи.
Насадок – это трубка цилиндрической или другой формы относительно малой длины в сравнении с диаметром. Через насадок происходит истечение жидкости из одной полости в другую или в окружающую среду. Характер течения жидкости в отверстиях насадках достаточно сложный. Расчёт средней скорости течения жидкости через насадки и отверстия выполняется с помощью эмпирического коэффициента скорости φ. Для расчёта расхода жидкости при течении через отверстия или насадки используется коэффициент расхода μ. Коэффициенты φ и µ учитывают:
- сжатие струи в её поперечном сечении при течении через отверстие или насадок;
- потери энергии, вызванные вязким трением;
- неравномерность эпюры скоростей потока в поперечном сечении струи. Неравномерность эпюры скоростей потока является причиной различия действительной кинетической энергии струи и энергии, рассчитанной по средней скорости потока. Учёт этого явления осуществляется с помощью коэффициента Кориолиса α. При ламинарном течении α = 2, а при турбулентном – α ≈ 1 – 1,3.
Теоретической основой для расчёта средней скорости потока и его расхода служит уравнение Бернулли для вязкой жидкости, учитывающее перечисленные особенности представления о течении жидкости через насадки и отверстия.
Уравнение средней скорости потока жидкости через отверстие или насадок имеет вид
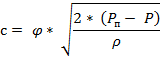
Объёмный расход жидкости при истечении через отверстие или насадок рассчитывается по зависимости
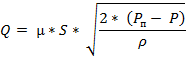
В этих уравнениях
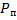 - полное давление жидкости в сечении перед отверстием;
- полное давление жидкости в сечении перед отверстием;
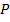 – статическое давление жидкости в сечении после отверстия;
– статическое давление жидкости в сечении после отверстия;
S – поперечное сечение отверстия или насадка.
В случае, когда перемещение поршня гидроцилиндра под действием силы F сопровождается истечением жидкости через насадок эти зависимости принимают вид
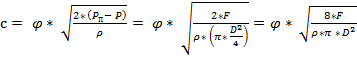 =
=
и
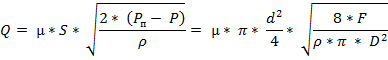
В этих уравнениях:
D – диаметр поршня;
d – внутренний диаметр насадка или отверстия.
Скорость движения поршня определим из уравнения неразрывности
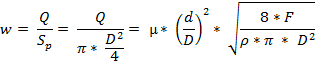
Здесь 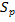 - площадь поверхности торца поршня.
- площадь поверхности торца поршня.
Ответы.
| Величина | Варианты | |||||||||
| W, мм/с | 17.2 |
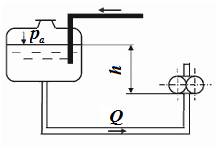 дом в центробежный насос при подаче Q и высоте всасывания h. Всасывающую трубу, длина которой l, диаметр d, считать гидравлически гладкой. Учесть сопротивление приемного клапана с фильтрующей сеткой ζ ф = 3. Вязкость жидкости ν = 0,006 Ст, ее плотность ρ = 750 кг/м3. Скоростным напором при входе в насос пренебречь. Атмосферное давление соответствует 750 мм.рт.ст. (Рис. к задаче 5.5)
дом в центробежный насос при подаче Q и высоте всасывания h. Всасывающую трубу, длина которой l, диаметр d, считать гидравлически гладкой. Учесть сопротивление приемного клапана с фильтрующей сеткой ζ ф = 3. Вязкость жидкости ν = 0,006 Ст, ее плотность ρ = 750 кг/м3. Скоростным напором при входе в насос пренебречь. Атмосферное давление соответствует 750 мм.рт.ст. (Рис. к задаче 5.5)
| Величина | Варианты | |||||||||
| Q, л/с | 0,2 | 0,3 | 0,4 | 0,6 | 6,7 | |||||
| h , м | 0,7 | 0,8 | 0,6 | 0,8 | 1,2 | |||||
| l, м | 6,5 | 7,6 | 6,4 | 4,5 | 2,2 | 2,5 | ||||
| d, мм |
Пример решения задачи.
Выберём два характерных горизонтальных сечения модели и запишем, используя эти сечения, уравнение Бернулли (уравнение сохранения энергии вязкой жидкости).
Первое сечение проведём через патрубок на входе в насос, а второе выберём совпадающим со свободной поверхностью жидкости в баке. Отсчёт геометрической высоты расположения жидкости в модели будем проводить от сечения на входе в насос. Тогда, геометрическая высота h способствует увеличению давления на входе в насос и расходуется на преодоление потерь напора жидкости от верхнего сечения до нижнего. Эти потери обусловлены вязким трением при течении жидкости через фильтр на входе в насос (не показан на рис.) и трением при течнии жидкости по трубе. Уравнение Бернулли запишем, как это оговорено в условии, без учёта скоростного напора жидкости на входе в насос.
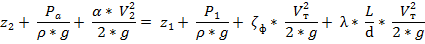
В этом уравнении α – коэффициент Кориолиса (см. задачу 3с.1).
По условию задачи
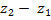 = h, а скорость жидкости в её свободной поверхности в баке равна нулю из-за большой поверхности этого сечения. Поэтому
= h, а скорость жидкости в её свободной поверхности в баке равна нулю из-за большой поверхности этого сечения. Поэтому
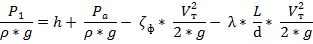
Это уравнение содержит все известные из условия параметры для расчёта абсолютного давления на входе в насос - 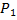 . Исключение составляет только лишь коэффициент гидравлического трения в трубе. Определим этот параметр. Из уравнения неразрывности получим значение скорости жидкости в трубе
. Исключение составляет только лишь коэффициент гидравлического трения в трубе. Определим этот параметр. Из уравнения неразрывности получим значение скорости жидкости в трубе
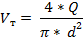
В этом уравнении 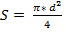 - площадь поперечного сечения трубы.
- площадь поперечного сечения трубы.
Тогда число Рейнольдса при течении жидкости в трубе может быть рассчитано по зависимости
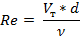
Теперь, используя приведенную в задаче 5с.1 таблицу, по известному значению числа Рейнольдса рассчитываем коэффициент гидравлического трения в трубе. В соответствии с условием задачи труба гидравлически гладкая. Поэтому используем следующие зависимости для расчёта коэффициента гидравлического трения 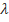 .
.
1. При изменении числа Рейнольдса в диапазоне 0<Re<2300 -
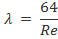
2. При изменении числа Рейнольдса в диапазоне 2300<Re<4000 -

3. При значении числа Рейнольдса 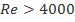 - используем формулу Блазиуса –
- используем формулу Блазиуса –
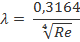
Полученное ранее уравнение для абсолютного давления жидкости на входе в насос приведём к виду
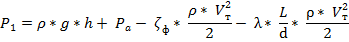
Прежде чем выполнить вычисления переведём единицу измерения кинематической вязкости из Ст в единицу вязкости 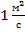 , а давление в мм. Hg в Па. Для этого используем зависимости
, а давление в мм. Hg в Па. Для этого используем зависимости
1 Ст = 1 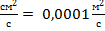
и
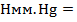
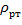 * g * H = 13600 * 9,81 *0,75 = 13600*100062 Па.
* g * H = 13600 * 9,81 *0,75 = 13600*100062 Па.
Выполним вычисления.
Ответы.
| Величина | Варианты | |||||||||
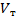 , м/с , м/с
| 2,55 | |||||||||
| Re, - | ||||||||||
| λ, - | 0,0220 | |||||||||
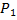 , кПа , кПа
|
| <== предыдущая | | | следующая ==> |
| Спектральный метод расчета надежности при перемежающихся отказах | | | Предмет исследования истории экономических учений |
Date: 2015-07-23; view: 1856; Нарушение авторских прав