
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема Коши́ о среднем значении
|
|
Пусть даны две функции 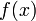 и и 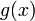 такие, что: такие, что:
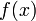 и и 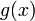 определены и непрерывны на отрезке определены и непрерывны на отрезке 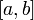 ;
производные ;
производные 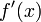 и и 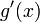 конечны на интервале конечны на интервале 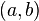 ;
производные ;
производные 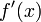 и и 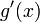 не обращаются в нуль одновременно на интервале не обращаются в нуль одновременно на интервале 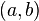
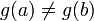 ;
тогда существует ;
тогда существует 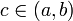 , для которой верно: , для которой верно:
 .
(Если убрать условие 4, то необходимо, например, усилить условие 3: g'(x) не должна обращаться в нуль нигде в интервале .
(Если убрать условие 4, то необходимо, например, усилить условие 3: g'(x) не должна обращаться в нуль нигде в интервале 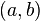 .) .)
|
Геометрически это можно переформулировать так: если 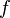 и
и 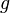 задают закон движения на плоскости (то есть определяют абсциссу и ординату через параметр
задают закон движения на плоскости (то есть определяют абсциссу и ординату через параметр 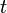 ), то на любом отрезке такой кривой, заданном параметрами
), то на любом отрезке такой кривой, заданном параметрами 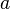 и
и 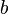 , найдётся касательный вектор, коллинеарный вектору перемещения от
, найдётся касательный вектор, коллинеарный вектору перемещения от 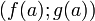 до
до 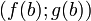 .
.
Доказательство
Для доказательства введём функцию
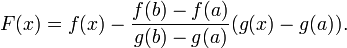
|
Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны 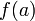 . Воспользовавшись упомянутой теоремой, получим, что существует точка
. Воспользовавшись упомянутой теоремой, получим, что существует точка  , в которой производная функции
, в которой производная функции 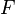 равна нулю, а
равна нулю, а 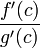 равна как раз необходимому числу.
равна как раз необходимому числу.
25) Правило Бернулли[1]-Лопита́ля — метод нахождения пределов функций, раскрывающий неопределённости вида 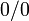 и
и 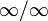 . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных
. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных
- Если
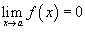 и
и 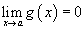 , то
, то 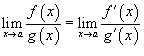 ;
; - Если
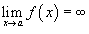 и
и 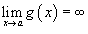 , то аналогично
, то аналогично 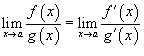 .
.
Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:
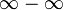
| 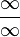
| 
| 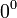
| 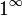
| 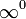
| 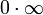
|
по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.
26)Для того чтобы диффернецируемая в интервале(а,b) функция у=f(x) была в этом интервале монотонной, необходимо и достаточно, чтобы в этом интервале её первая производная сохраняла знак, а именно:
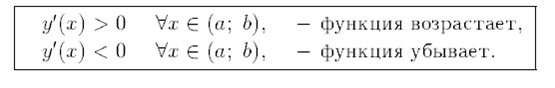
Функция называется возрастающей на интервале [а,b] если большему значению аргумента соответствует большее значение функции.
Функция называется убывающей на интервале [а,b] если большему значению аргумента соответствует меньшее значение функции.
27) 


28) 



29) 


31)

Date: 2015-07-23; view: 622; Нарушение авторских прав