
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Производная частного функций
|
|
Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле
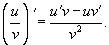
Сложная функция – функция от функции. Если z – функция от у, т.е. z (y), а у, в свою очередь, – функция от х, т.е. у (х), то функция f (x) = z (y(x)) называется сложной функцией (или композицией, или суперпозицией функций) от х.
производная сложной функции: 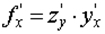
15) Дифференцирование сложных логарефмисеких функций
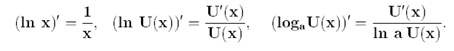
Дифференцирование сложной степенной функции 
16) Производная основных элементарных функций
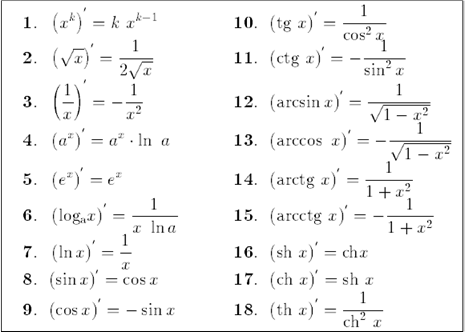
17) Производная обратной функции
Пусть функция 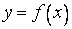 строго возрастает, непрерывна на интервале
строго возрастает, непрерывна на интервале 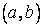 и имеет конечную не равную нулю производную
и имеет конечную не равную нулю производную 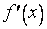 в некоторой точке
в некоторой точке 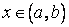 . Тогда обратная для
. Тогда обратная для 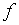 функция
функция 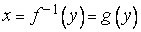 также имеет производную в соответствующей точке, определяемую равенством
также имеет производную в соответствующей точке, определяемую равенством
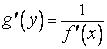 (1)
(1)
или
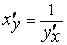 (1’)
(1’)
Д о к а з а т е л ь с т в о. Как нам известно, обратная функция 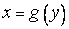 строго возрастает и непрерывна на интервале
строго возрастает и непрерывна на интервале  , где
, где
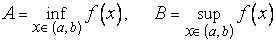
(см. § 3.6, теорема 1’).Дадим рассматриваемому 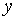 приращение
приращение  . Ему соответствует приращение
. Ему соответствует приращение 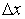 обратной функции, также не равное нулю в силу строгой монотонности
обратной функции, также не равное нулю в силу строгой монотонности 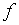 . Поэтому
. Поэтому
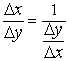 .
.
Если теперь 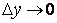 , то в силу непрерывности
, то в силу непрерывности 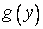 приращение
приращение 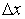 также
также  ; но при
; но при 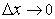
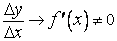 , следовательно, существует предел
, следовательно, существует предел
 .
.
Этим формула (1) доказана.
П р и м е ч а н и е. Если 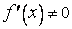 непрерывна на
непрерывна на 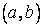 , то
, то 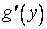 непрерывна на
непрерывна на  .Это следует из (1), где можно положить
.Это следует из (1), где можно положить 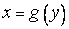 :
:
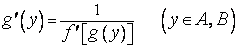 .
.
Ведь сложная функция 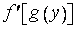 , состоящая из непрерывных функций
, состоящая из непрерывных функций 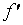 и
и 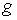 , непрерывна.
, непрерывна.
Свойства взаимно обратных функций 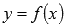 и
и  .
.
1) 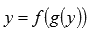 и
и 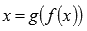
2)Из первого свойства видно, что область определения функции 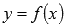 совпадает с областью значений функции
совпадает с областью значений функции  и наоборот.
и наоборот.
3)Графики взаимно обратных функций симметричны относительно прямой y=x.
4)Если 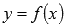 возрастает, то и
возрастает, то и  возрастает, если
возрастает, если 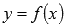 убывает, то и
убывает, то и  убывает.
убывает.
18) Обра́тныетригонометри́ческиефу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям.

Таким образом, при дифференцировании сложной обратной тригонометрической функции нужно сначала продифференцировать её как обычную обратную тригонометрическую функцию, а затем умножить на производную аргумента этой функции
19) Показательная функции: y=ax, a>0, a(не равна 1)
x=logay
(аx)'=ахlпа
(ех)' = ех
ax = (eln a)x = ex ln a
20) Логарифмическое дифференцирование:
Правило логарифмического дифференцирования состоит в том, что производная функции может быть найдена как произведение самой функции на производную её натурального логарифма
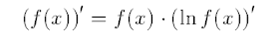
Производная показательно-степенной функции:
Прием логарифмического дифференцирования очень эффективен при дифференцировании показательно-степенной функции 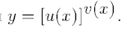 .
.
Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основаниеи показатель степени зависят от переменной, то такая функция будет показательно – степенной.
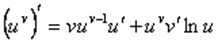
21) Дифференциал функции:
Дифференциал функции y=f(x) в точке х называется главная линейная часть её приращения y=f(x).
Дифференциал обозначается символом dy.
Формулы вычисления дифференциала:
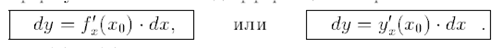
Геометрический смысл дифференциала - приращение ординаты касательной к графику функции в точке с абсциссой Х

·
Дифференциал постоянной равен нулю:
dc = 0, с = const.
· Дифференциал суммы дифференцируемых функций равен сумме дифференциалов слагаемых:
· d(u+v)=du + dv
Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны
· d(u+c) = du (c= const).
· Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой:
· d(uv) = udv + vdu.
Следствие. Постоянный множитель можно выносить за знак дифференциала
· d(cu) = cdu (с = const).
· Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой
· 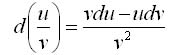
· Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной на дифференциал аргумента независимого от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.
Инвариантность: Формула первого дифференциала справедлива для случая сложной функции 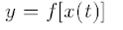
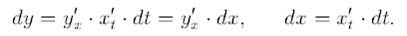
Несмотря на то, что дифференциал и производная функции отличаются лишь множителем dx или 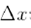 сеть их разная.
сеть их разная.
22) Параметрическая функция и её дифференцирование:
Пусть функция у(х) задана параметрически
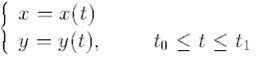
Причем х(t) и y(t)- дифференцируемые в интервале [t0;t1] функции, и х(t) имеет обратную дифференцируемую функцию t(x). Тогда имеет место формулы для нахождения производной функции у по независимой переменной х и х по у.

Эти формулы дают возможность находить производные параметрически заданных функций, не находя выражения непосредственной зависимости у от х.
23) Гиперболи́ческиефу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.
Гиперболические функции задаются следующими формулами:
· гиперболический синус:
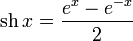
· гиперболический косинус:
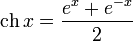
· гиперболический тангенс:
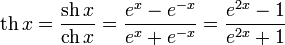
· гиперболический котангенс:
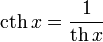
· гиперболические секанс и косеканс:
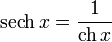
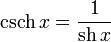
24) Теорема Ро́лля (теорема о нуле производной) утверждает, что
Если вещественная функция, непрерывная на отрезке 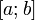 и дифференцируемая на интервале и дифференцируемая на интервале 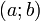 , принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю. , принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.
|
Доказательство
Если функция на отрезке постоянна, то утверждение очевидно, поскольку производная функции равна нулю в любой точке интервала.
Если же нет, поскольку значения функции в граничных точках сегмента равны, то согласно теореме Вейерштрасса, она принимает своё наибольшее или наименьшее значение в некоторой точке интервала, то есть имеет в этой точке локальный экстремум, и по лемме Ферма, в этой точке производная равна 0.
Теорема Лагранжа:
Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция 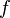 непрерывна на отрезке
непрерывна на отрезке 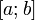 и дифференцируема в интервале
и дифференцируема в интервале 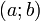 , то найдётся такая точка
, то найдётся такая точка 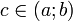 , что
, что
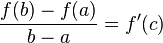 .
.
Date: 2015-07-23; view: 5414; Нарушение авторских прав