Дифференциальное уравнение

- это уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значения её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, ее производные и независимые переменные.

Все дифференциальные уравнения можно разделить на обыкновенные дифференциальные уравнения(ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Порядком или степенью дифференциального уравнения называется наибольший порядок производных, входящих в дифференциальное уравнение.

Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени. Формулировка второго закона Ньютона для материальной точки дает простейший пример обыкновенного дифференциального уравнения второго порядка с неизвестной функцией координат точки и временем, выступающим в роли независимой переменной.

Обыкновенное дифференциальное уравнение (ОДУ) n-ого порядка — это уравнение вида 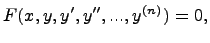где — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной 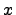, штрих означает дифференцирование по .

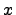Решением дифференциального уравнения называется 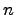раз дифференцируемая функция , удовлетворяющая уравнению во всех точках своей области определения. Обычно существует целое множество таких функций (такое параметризованное семейство рещений называется общим решением дифференциального уравнения), и для выбора одного из них требуется наложить на него дополнительные условие: например, потребовать, чтобы решение принимало в данной точке данное значение. Полученное единственное решение называется частным решением. Общее решение обыкновенного дифференциального уравнения n -ого порядка может быть выражено в ви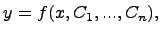де где 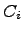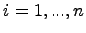- произвольные постоянные. Если общее решение задано в неявном виде выражением 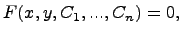то это выражение называют общим интегралом дифференциального уравнения.

Date: 2015-07-22; view: 403; Нарушение авторских прав