Разветвленные цепи. Правила Кирхгофа

На практике часто требуется рассчитать разветвленную цепь.

Это цепь, содержащая несколько ветвей.

Ветвь образуется одним или несколькими последовательно соединенными участками цепи.

Место соединения трех или более ветвей называется узлом.

Ветви, присоединенные к одной паре узлов, называются параллельными.

Любой замкнутый путь, проходящий по нескольким ветвям, называется контуром.

Рассчитать электрическую цепь – означает вычислить токи во всех ее ветвях по известным значениям сопротивлений и ЭДС, действующих в ветвях.

Этот расчет упрощается, если использовать правила Кирхгофа.

1. Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю: 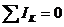. (4)

· Если ток направлен к узлу, он входит в выражения (4) со знаком «+».

· Если от узла – со знаком «-».

Это правило вытекает из уравнения непрерывности, т.е. в конечном счете, из закона сохранения заряда.

Действительно, для постоянного тока ,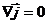

тогда поток вектора 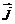через любую замкнутую поверхность, окружающую узел, равна нулю.

Но поток 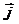равен алгебраической сумме токов, сходящихся в узле, следовательно, .

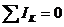2. Второе правило относится к любому выделенному в разветвленной цепи замкнутому контуру и является обобщением закона Ома на разветвленные цепи: 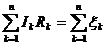(5)

- сумма падений напряжений на всех участках замкнутого контура равна алгебраической сумме ЭДС, действующих в этом контуре.

- Здесь n – число участков, на которые контур разбивается узлами,

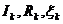- - соответственно, сила тока, сопротивление и ЭДС k -того участка.

Для составления уравнений (5) необходимо

· произвольно выбрать направление обхода контура (по часовой стрелке или против нее). Все токи на участках, совпадающие с направлением обхода, считают положительными, несовпадающие – отрицательными.

· учитывать правило знаков для ЭДС источников: если напряженность поля сторонних сил в источнике совпадает с направлением обхода участка (т.е. внутри источника обход связан с перемещением положительных зарядов от катода к аноду), то при подсчете ЭДС этого источника считают положительной, в противном случае – отрицательной. Если какая-то ЭДС повышает потенциал в направлении обхода, её надо брать со знаком плюс, в противном случае – со знаком минус.

· При расчете разветвленных цепей постоянного тока рекомендуется:

- произвольно выбрать и обозначить на схеме цепи направления токов во всех участках цепи (если в результате вычисления окажется, что такой ток положителен, то значит, что его направление выбрано правильно, если же ток окажется отрицательным, то его истинное направление противоположно направлению стрелки);

- для каждого участка цепи записать уравнение для токов по первому правилу Кирхгофа;

- выделить в разветвленной цепи всевозможные замкнутые контуры, в каждом контуре произвольно выбрать направления обхода и записать уравнения для напряжений по второму правилу Кирхгофа; при составлении уравнений контуры следует выбирать так, чтобы каждый новый контур содержал хотя бы один участок цепи, не входящий в уже рассмотренные контуры;

- из записанных уравнений выбрать k любых независимых уравнений (k – число неизвестных токов); решая полученную систему, найти значения токов;

- если в результате расчета получается отрицательное значение силы тока на каком-либо участке цепи, это означает, что электрический ток в действительности идет в направлении, противоположном выбранному при расчете.

Уравнений надо составлять столько, чтобы их число было равно числу искомых величин. При этом надо следить, чтобы одни уравнения не являлись следствием других:

1) если в разветвленной цепи имеется N узлов, то независимые уравнения типа 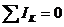можно составить лишь для N —1 узлов - уравнение для последнего узла будет следствием предыдущих;

2) если в разветвленной цепи можно выделить несколько замкнутых контуров, то независимые уравнения типа 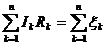можно составить только для тех контуров, которые не получаются в результате наложения уже рассмотренных.

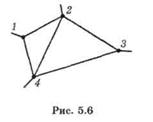
Например, для цепи (рис. 5.6)

· такие уравнения для контуров 124 и 234 будут независимыми.

· Уравнение же для контура 1234 является следствием двух предыдущих.

Можно составить независимые уравнения для двух других контуров,

например

· для контуров 124 и 1234,

· но тогда уравнение для контура 234 будет следствием двух первых.

Число независимых уравнений типа 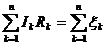оказывается равным наименьшему числу разрывов, которые следует сделать в цепи, чтобы нарушить все контуры. Это число, кстати, равно числу областей, ограниченных проводниками, если схему удастся изобразить на плоскости без пересечений.

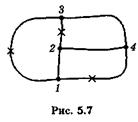
Например, для цепи (рис. 5.7), содержащей четыре узла, надо составить три уравнения типа 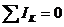и три уравнения типа 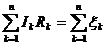, ибо минимальное число разрывов (они помечены кре­стиками), нарушающее все контуры, равно трем (трем равно и число областей).

Если неизвестными являются токи, то их число равно шести — по числу отдельных участков между узлами, что соответствует числу независимых уравнений.

Пример:

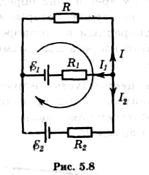Найти силу тока и его направление через сопротивление R в схеме (рис. 5.8). Все сопротивления и э. д. с. предполагаются известными.

Здесь три участка, следовательно, три неизвестных тока I₁, I₂ и I Обозначим стрелками (не задумываясь) их предположительные направления (у правого узла).

Цепь содержит N = 2 узла. Значит, независимых уравнений типа 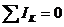только одно:

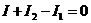
Теперь составим уравнения типа 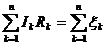— их должно быть два (по числу областей). Возьмем контур, содержащий R и R1 и контур с R и R2. Выбрав направление обхода каждого контура по часовой стрелке, запишем

,

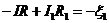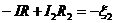
Полезно убедиться, что соответствующее уравнение для контура, содержащего R1 и R2, является следствием этих двух. Решив систему написанных трех уравнений, получим

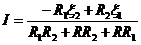
Если после подстановки числовых значений окажется, что I > 0, то это значит, что в действительности ток течет так, как мы предположили на рис. 5.8, если же I < О, то в противоположном направлении.

Date: 2015-07-22; view: 1002; Нарушение авторских прав