Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Закон Ома. Сопротивление
|
|
Закон Ома был экспериментально открыт в 1826 году в следующей форме:
Сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике:
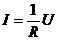, (1) - закон Ома в интегральной форме
где R электрическое сопротивление проводника,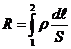 
,
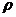- удельное сопротивление (Ом м), 
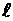- длина, S – площадь сечения проводника.
Однородным называется такой участок цепи, на котором действуют только электростатические силы.
Выражение (1) определяет соотношение между током и напряжением для однородного участка цепи и называется законом Ома в интегральной форме.
Единица сопротивления – Ом,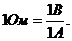 
Сопротивление проводника определяется
· его геометрическими размерами (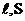
)
· материалом, их которого этот проводник изготовлен.
Наименьшими удельными сопротивлениями обладают серебро, медь, золото, алюминий.
Величина, обратная удельному сопротивлению, называется удельной проводимостью или электропроводимостью вещества.
В дифференциальной форме закон Ома принимает вид: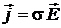 
- вектор плотности тока равен произведению электропроводности и вектора напряженности электростатического поля.
- 
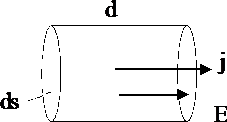
Рассмотрим однородный участок проводника, в пределах которого площадь сечения остается постоянной.
· сила тока равна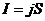 
,
· связь напряженности и потенциала дает значение напряжения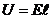 
,
· сопротивление участка определяется формулой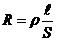 
.
· Подставив в формулу (1), имеем: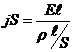 
;
отсюда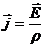 
или
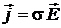
Закон Ома объясняет классическая теория металлов, созданная физиками Друде и Лоренцем. Согласно этой теории валентные электроны в металле являются общими для всех атомов и движутся в пространстве между положительными ионами, которые находятся в узлах кристаллических решеток. Электроны проводимости образуют электронный газ, подчиняющийся законам идеального газа. Однако, в отличие от молекул идеального газа, которые при движении сталкиваются друг с другом, электроны в металле сталкиваются с узлами кристаллической решетки, и расстояние, которое проходит электрон между двумя такими соударениями, есть длина свободного пробега электрона λ. В результате таких столкновений устанавливается тепловое равновесие между электронным газом и кристаллической решеткой. Друде распространил на электронный газ результаты кинетической теории газов.
Тогда средняя скорость теплового движения электронов: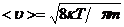 
,
при комнатной температуре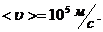 
При внесении проводника в поле, на хаотическое тепловое движение электронов накладывается упорядоченное движение электронов некоторой средней скоростью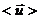 
,
при этом плотность тока: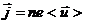 
.
Максимально возможное значение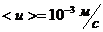 
,
т.е. в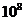 
раз меньше средней скорости теплового движения 
.
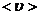Найдем изменение кинетической энергии электронов, вызываемое полем.
Для этого определим средний квадрат результирующей скорости:
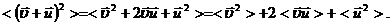
Величины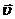 
и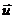 
независимы, поэтому 
,
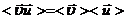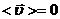(среднее значение вектора тепловой скорости равно нулю, т.к. направление меняется хаотично), следовательно,
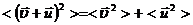
Таким образом, упорядоченное движение увеличивает кинетическую энергию электронов на
.
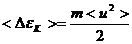Двигаясь в кристалле, электроны испытываю соударение с узлами кристаллической решетки. Время между двумя соударениями: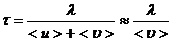 
,
где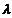 
-длина свободного пробега электрона в металле.
Друде предположил, что при соударении электронов с узлом кристаллической решетки вся дополнительная энергия передается иону, в результате соударения u =0. Если поле, ускоряющее электроны, однородно, электрон получает постоянное ускорение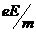 
, и к концу пробега скорость упорядоченного движения достигает максимума:
.
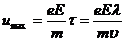Скорость u изменяется во времени линейно, поэтому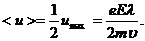 
Для плотности тока j получим: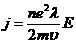 
, т.е. j ~ E - закон Ома.
Коэффициент пропорциональности есть проводимость.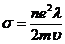 
Если бы электроны не сталкивались с ионами кристаллической решетки, их скорости росли бы беспрепятственно, и проводимость была бы неограниченно большой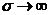 
, т.к. 
.
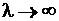Сопротивление проводника зависит от температуры и давления.
Сопротивление металлических проводников зависит от температуры по закону: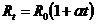 
,
где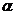 
- температурный коэффициент сопротивления.
Изобразим эту зависимость графически.
Для некоторых металлов и сплавов вблизи абсолютного нуля температуры наблюдается скачкообразное падение сопротивления практически до нуля. Это явление называют сверхпроводимостью .
Температура перехода в сверхпроводящее состояние
для разных металлов лежит в интервале от 2 до 10 К.
4. Закон Ома для неоднородного участка цепи.
На носители тока на неоднородном участке цепи
· действуют, кроме электростатических сил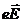 
, еще и сторонние силы 
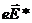. Сторонние силы способны вызывать упорядоченное движение носителей тока так же, как и силы электростатические.
· средняя скорость упорядоченного движения носителей пропорциональна суммарной силе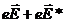 
, тогда плотность тока
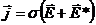(2)
– это закон Ома для неоднородного участка цепи в дифференциальной форме.
Неоднородным называют участок цепи, на котором действуют сторонние силы.
Перейдем к интегральной форме этого закона.
Рассмотрим неоднородный участок цепи.
· Допустим, что внутри этого участка существует линия (контур тока) удовлетворяющая следующим условиям:
1) в каждом сечении, перпендикулярном к контуру, величины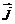 
, 
, 
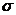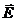и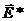 
имеют с достаточной точностью одинаковые значения;
2) векторы 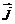, , 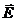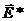в каждой точке направлены по касательной к контуру. Поперечное сечение проводника может быть непостоянным.
· Выберем произвольно направление движения по контуру.
Пусть выбранное направление соответствует перемещению от конца 1 к концу 2 участка цепи. Спроектируем выражение (2) на элемент контура1-2:
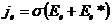, (3)
причем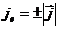 
; 
; 
.
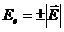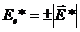Знак ‘+’ берем в том случае, если ток течет от 1 к 2,
‘-‘ если ток течет в направлении 2 к 1.
Вследствие сохранения заряда сила постоянного тока в каждом сечении должна быть одинаковой.
Поэтому вдоль контура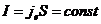 
.
Силу тока в данном случае нужно рассматривать как алгебраическую величину.
Направление 1-2 выбрано произвольно, поэтому, если ток течет в выбранном направлении, его считают положительным, если в направлении 2-1 – отрицательным.
· Заменим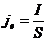 
; 
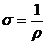, имеем из (3):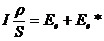 
· Умножим это выражение на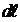 
и проинтегрируем вдоль контура: 
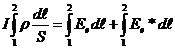, здесь 
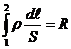– сопротивление всей цепи,
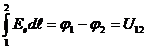- падение напряжения на сопротивление R,
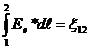- ЭДС, действующая на участки 1,2.
Тогда 
, - интегральная форма закона Ома для неоднородного участка цепи
а ток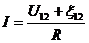 
- это закон Ома для неоднородного участка цепи.
1) Если цепь замкнутая, то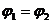 
; и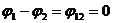 
.
Тогда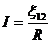 
-закон Ома для замкнутой цепи.
2) если источник разомкнут, то I =0 и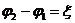 
, т.е. ЭДС источника можно определить как разность потенциалов на его клеммах в разомкнутом состоянии.
3) Если в цепи действует несколько ЭДС, то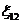 
равна их алгебраической сумме.
Примеры:
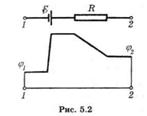
- Рассмотрим участок цепи, показанный на рис. 5.2.
Сопротивление отлично от нуля только на отрезке R.
На нижней части рисунка представлен ход потенциала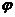 
вдоль данного участка.
Выясним, что здесь происходит.
Из того факта, что потенциал на отрезке R уменьшается слева направо, следует, что I > 0, т. е. ток течет в положительном направлении (от 1 к 2).
В данном случае 
< 
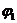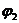, но ток течет от точки 1 к точке 2 — в сторону большего значения потенциала. Это возможно лишь потому, что на данном участке имеется э. д. с., действующая в положительном направлении (от 1 к 2).
Пример 2.
Внешнее сопротивление в цепи в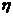 
раз больше внутреннего сопротивления источника. Найти отношение разности потенциалов на клеммах источника к его ЭДС.
Пусть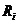 
- внутреннее сопротивление источника, а 
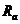- внешнее сопротивление цепи. Согласно формуле получаем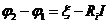 
Согласно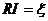 
получаем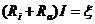 
Из этих двух уравнений получим: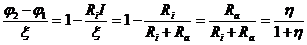 
Отсюда видно, что чем больше 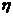, тем больше приближается разность потенциалов на клеммах источника к его э. д. е., и наоборот.
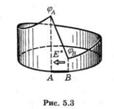
В заключение полезно привести наглядную картину, позволяющую лучше уяснить, что происходит в замкнутой цепи постоянного тока.
На рис. 5.3 показано распределение потенциала 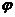вдоль замкнутой цепи, содержащей источник э. д. с. на участке АВ. Потенциал 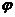для наглядности отложен вдоль образующих цилиндрической поверхности, которая опирается на контур с током.
Точки А и В соответствуют положительной и отрицательной клеммам источника.
Из рисунка видно, что процесс протекания тока можно представить себе так: положительные заряды-носители «соскальзывают» по наклонному «желобу» от точки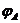 
к точке 
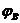— по внешнему участку цепи, внутри же источника «подняться» от точки 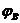к точке 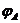им помогают сторонние силы, обозначенные стрелкой.
Date: 2015-07-22; view: 463; Нарушение авторских прав