Формулировки логических законов. 1. Закон двойного отрицания:

1. Закон двойного отрицания:

.

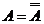Двойное отрицание исключает отрицание.

2. Переместительный (коммутативный) закон:

• для логического сложения:

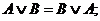
• для логического умножения:

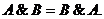
Результат операции над высказываниями не зависит от того,
в каком порядке берутся эти высказывания. В обычной алгебре
а + b = b + а, а × b = b × а.

3. Сочетательный (ассоциативный) закон:

• для логического сложения:

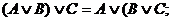
• для логического умножения:

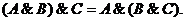
При одинаковых знаках скобки можно ставить произвольно или вообще опускать. В обычной алгебре

(А + B) + С = А + (B + С) = А + B + С,

А × (B × С) = А × (B × С) = А × B × С.

4. Распределительный (дистрибутивный) закон:

• для логического сложения:

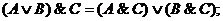
• для логического умножения:

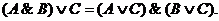
Закон определяет правило выноса общего высказывания за скобку.

В обычной алгебре .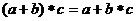

5. Закон общей инверсии (законы де Моргана):

• для логического сложения:

;

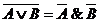• для логического умножения:

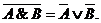
6. Закон идемпотентности (от латинских слов idem — «тот же самый» и potens — «сильный»; дословно — «равносильный»):

• для логического сложения:

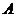Ú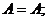

• для логического умножения:

.

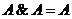Закон означает отсутствие показателей степени

7. Законы исключения констант:

• для логического сложения:

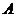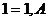Ú Ú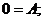

• для логического умножения:

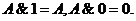
8. Закон противоречия:

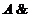
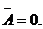
Невозможно, чтобы противоречивые высказывания были одновременно истинными.

9. Закон исключения третьего:

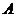Ú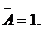

Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.

10. Закон поглощения:

• для логического сложения:

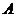Ú

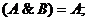
• для логического умножения:

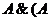Ú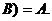

11. Закон исключения (склеивания):

• для логического сложения:

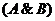Ú

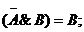
• для логического умножения:

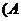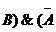Ú Ú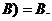

12. Закон контрапозиции (правило перевертывания):

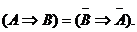
Переместительный, сочетательный (для логических сложения и умножения) и распределительный (для логического сложения) законы имеют полную аналогию с обычной алгеброй. Для других законов такой аналогии нет.

Date: 2015-07-22; view: 418; Нарушение авторских прав