Основные сведения. В анизотропных средах, к которым относятся намагниченные ферриты и плазма, проявляются новые свойства ЭМВ

В анизотропных средах, к которым относятся намагниченные ферриты и плазма, проявляются новые свойства ЭМВ, – существенные отличия условий распространения ЭМВ в прямом и обратном направлении в линии связи.

Феррит обладает магнитными свойствами ферромагнетика и электрическими свойствами диэлектрика. Это достигается смешиванием частиц ферромагнетика с диэлектическим материалом при изготовлении. ЭМП, проникая в диэлектрик, взаимодействует с ферромагнетиком. В диапазоне СВЧ типичные параметры ферритов таковы: e = 5–20; m = 10–2000; s = 10^–7–10^–12 См/м; tg d = 10^–4 [2, 10].

Зависимость параметров феррита от напряженности внешнего (подмагничивающего) магнитного поля позволяет создавать невзаимные СВЧ устройства (вентили, циркуляторы, переключатели, невзаимные фазовращатели и т. п.) [2, 10].

Явления ферромагнетизма имеют квантовую природу, в классической электродинамике используют приближенные методы их анализа.

Плазмой называют электрически нейтральный, частично ионизированный газ. При появлении внешнего (подмагничивающего) магнитного поля, как и в ферритах, проявляется анизотропия. Данное явление необходимо учитывать при распространении радиоволн в ионосфере.

Параметры анизотропных сред (в общем случае – m, e, s) становятся тензорными величинами. Тензор представляет собой матрицу, несимметричную относительно диагоналей. Рассмотрим физические основы проявления анизотропии ферритов в подмагничивающем внешнем поле .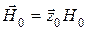

Электрон, обладающий одновременно механическим и магнитным моментами, подобен волчку. Заряд электрона – отрицательный, поэтому эквивалентный ток электрона течет в направлении, противоположном его вращению, и в итоге магнитный и электрический моменты противоположны по направлению.

При появлении внешнего подмагничивания поле стремится направить магнитный момент к оси вращения электрона, сориентировав его по полю. Однако из-за гироскопических свойств ось волчка не совмещается с направлением подмагничивающего поля (ось z), а прецессирует (вращается с сохранением угла между осью волчка и осью z) относительно оси z, описывая конус:

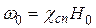, (13.1)

где w ₀ – циклическая частота прецессии; 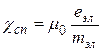= 7p×10⁴ м/Кл.

В реальных ферритах есть магнитные потери, поэтому прецессия имеет затухающий характер и заканчивается совпадением магнитного момента с .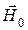

Рассмотрим распространение в феррите гармонической ЭМВ с частотой w, причем амплитуда ее магнитной компоненты 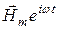много меньше 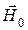. После разложения (1.1) в ДСК на скалярные уравнения с учетом соотношений для магнитных моментов получим тензор магнитной проницаемости :

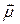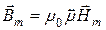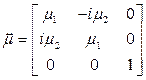, , (13.2)

где m ₁ = 1 – 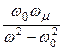; m ₂ = 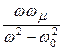; ; M ₀ – намагниченность [1].

Для анализа распространения ЭМВ в намагниченном феррите необходимо подставить полученные соотношения в систему уравнений Максвелла и найти g. После преобразований [2, 10] получим, что постоянные распространения b⁺ и b ^– для прямой и обратной ЭМВ, а значит, и фазовые скорости, отличаются:

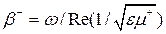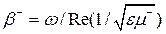; ; (13.3)

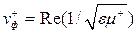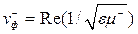; , (13.4)

где m ⁺ = m ₁ + m ₂; m ^– = m ₁ – m ₂ [2, 10].

ЭМВ с b⁺ называют левой, а с b ^– – правой.

Рассмотрим суперпозицию этих волн. Постоянная Фарадея

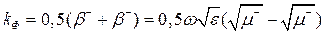(13.5)

позволяет записать результат в виде

. (13.6)

Из (13.6) следует, что ЭМВ является плоской, а вектор суммарного ЭМП будет поворачиваться при распространении ЭМВ вдоль оси z по мере ее продвижения.

При отсутствии внешнего подмагничивающего поля k_Ф = 0, правая и левая волны становятся одинаковыми, ЭМВ будет поляризована линейно.

Явлением (эффектом) Фарадея называют поворот плоскости поляризации ЭМВ в зависимости от координаты по мере продвижения вдоль оси z. Явление Фарадея необратимо, и феррит является невзаимной сре дой.

На рис. 13.1 приведены графики зависимости магнитных проницаемостей феррита (m ⁺= m ⁺’+ i m ⁺”; m ^–= m ^–’+ i m ^–”) от напряженности H₀ при фиксированной частоте. Из графиков видно, что для m ^– изменения незначительны, в то время как m ⁺’ и m ⁺” имеют ярко выраженный резонанс.

Явление резкого увеличения поглощения энергии ЭМВ, направление и частота которой совпадают с направлением и частотой прецессии, называется ферромагнитным резонансом. Поглощенная энергия тратится на поддержание прецессии (компенсация магнитных потерь) в феррите, поэтому данное явление называют также продольным гиромагнитным резонансом [2, 10].

Для прямой волны резонансное поглощение будет наблюдаться только для правой поляризации, а для обратной волны – только для левой поляризации.

При поперечном намагничивании феррита (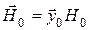) решениями волновых уравнений являются обыкновенная и необыкновенная волны.

ЭМП обыкновенной ЭМВ имеет магнитную составляющую, которая параллельна H₀. По своим свойствам эта волна не отличается от плоской однородной ЭМВ, распространяющейся в диэлектрике с теми же e, m и s, что и у феррита.

Необыкновенная волна имеет эллиптически поляризованное магнитное поле, поскольку кроме поперечной имеет еще и продольную компоненту 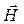. В этом проявляются гиротропные свойства феррита.

Чтобы найти характеристики необыкновенной ЭМВ, в (13.3)–(13.4) следует подставить эквивалентную магнитную проницаемость m _^ [2]

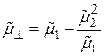. (13.7)

На рис. 13.2 приведены графики m _^’, m ⁺” и для сравнения m ⁺’, m ⁺”. Из графиков следует, что для необыкновенной волны наблюдается ферромагнитный резонанс, называемый поперечным гиромагнитным резонансом.

В дорезонансной (H₀ > H_{рез ^}) области 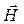описывает эллипс, вращаясь в положительном направ­лении относительно 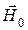(оси y), фазовая скорость необыкновенной ЭМВ больше чем обыкновенной. В зарезонансной (H₀ < H_{рез ^}) области 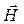описывает эллипс в отрицательном направлении относительно 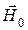, фазовая скорость необыкновенной волны меньше, чем обыкновенной. Поглощение при поперечном резонансе меньше, чем при продольном.

ЭМВ с плоскостью поляризации, не совпадающей с 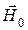, в поперечно намагниченном феррите распадается на обыкновенную и необыкновенную ЭМВ, их фазовые скорости в направлении распространения различны, и в общем случае ЭМВ имеет эллиптическую поляризацию.

Преобразование линейной поляризации в эллиптическую в поперечно-намагниченном феррите называют эффектом Коттона–Мутона.

При распространении ЭМВ в подмагниченной плазме наблюдаются похожие явления, но тензорной величиной становится диэлектрическая проницаемость .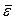

С помощью рассмотренного ранее принципа перестановочной двойственности (см. тему 11 (11.16)) задачи анализа распространения ЭМВ в феррите и плазме можно свести к единой модели [2, 10].

Список рекомендуемой литературы: [ 2, с. 439–476; 11, с. 187–205, 404–415; 5, с. 42–51, 303–318; 6, с. 506–536; 8, с. 157–170; 9, с. 377–408; 10, с. 377–408; 12, с. 204–206; 13, с. 180–187, 15 ].

Контрольные вопросы и задания

1. Дайте определение анизотропной среды. Приведите примеры таких сред.

2. Дайте определение гиротропной среды.

3. Что такое продольный ферромагнитный резонанс?

4. Дайте определение эффекту Фарадея и постоянной Фарадея.

5. Дайте характеристику магнитной проницаемости феррита.

6. Опишите свойства обыкновенной и необыкновенной ЭМВ в поперечно-намагниченном феррите.

7. Дайте характеристику поведения векторов ЭМП в феррите.

8. Дайте определение поперечного ферромагнитного резонанса.

9. Опишите эффект Коттона – Мутона.

10. Укажите возможные применения анизотропии ферритов в технике СВЧ.

Date: 2015-06-11; view: 651; Нарушение авторских прав