Межотраслевой баланс производства и выпуска продукции

Цель балансового анализа – ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производства каждой из п отраслей, чтобы удовлетворить все потребности в продукции этой отрасли? При этом каждая отрасль выступает, с одной стороны, как производитель некоторой

_________________________________________________________

продукции, а с другой – как потребитель продукции и своей, и произведенной другими отраслями.

Связь между отраслями, как правило, отражается в таблицах межотраслевого баланса, а математическая модель, позволяющая их анализировать, разработана в 1936 г. американским экономистом В.Леонтьевым.

Предположим, что рассматривается п отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.

Рассмотрим процесс производства за некоторый период времени (например, год).

Введем следующие обозначения: 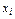– общий (валовой) объем продукции 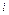- й отрасли ();

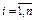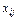– объем продукции 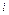- й отрасли, потребляемой 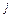- й отраслью в процессе производства ( ),

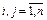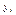– объем конечного продукта 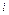- й отрасли для непроизводственного потребления.

Так как валовой объем продукции любой 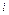- й отрасли равен суммарному объему продукции, потребляемой п отраслями, и конечного продукта, то

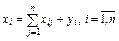(4)

Уравнения (4) называются соотношениями баланса. Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в (4), имеют стоимостное выражение.

Введем коэффициенты прямых затрат

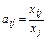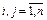, (), (5)

показывающие затраты продукции /-и отрасли на производство единицы продукции у-й отрасли.

Можно полагать, что в некотором промежутке времени коэффициенты 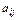будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат от валового выпуска, т.е.

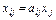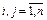, ( ) (6)

вследствие чего построенная на этом основании модель межотраслевого баланса получила название линейной.

Теперь соотношения баланса (4) примут вид:

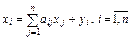(7)

Обозначим , , ,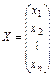

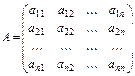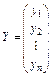где X – вектор¹ валового выпуска, Y – вектор конечного продукта, А – матрица прямых затрат (технологическая или структурная матрица).

Тогда систему (4) можно записать в матричном виде:

Х = AX + Y (8)

Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска X, который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукта Y.

Перепишем уравнение (8) в виде:

(Е - А)Х = Y. (9)

Если матрица (Е - А) невырожденная, т.е. 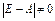, то по формуле (7)

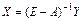(10)

Матрица 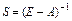называется матрицей полных затрат.

_________________________________________________________

Экономический смысл элементов матрицы 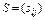: каждый элемент 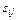матрицы S есть величина валового выпуска продукции 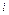-й отрасли, необходимого для обеспечения выпуска единицы конечного продукта 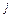-й отрасли .

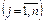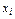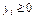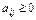В соответствии с экономическим смыслом задачи значения , должны быть неотрицательны при неотрицательных значениях и , где .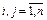

Матрица 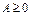называется продуктивной, если для любого вектора 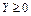существует решение 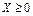уравнения (9). В этом случае и модель Леонтьева называется продуктивной.

Существует несколько критериев продуктивности матрицы А. Один из них говорит о том, что матрица А продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы, т.е. матрица А продуктивна, если 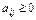для любых 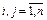и 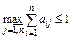и существует номер 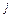такой, что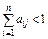

Конец.

Date: 2015-07-11; view: 325; Нарушение авторских прав