Определитель Слэйтера

Волновую функцию

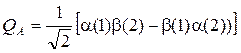
Можно формально переписать в виде:

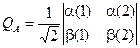
Такая запись носит название определителя Слэйтера и широко используется в квантовой механике и квантовой химии для конструирования и записи заведомо антисимметричной волновой функции.

Пусть у нас есть N ортонормированных функций j _i, каждая из которых зависит от четырех координат только одного электрона. Можно записать определитель вида:

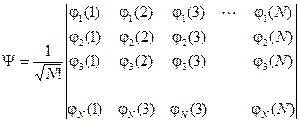
Раскрывая такой детерминант, мы получим линейную комбинацию N! возможных произведений. Легко видеть, что, обмену координат двух электронов соответствует перестановка двух столбцов определителя, которая немедленно дает смену знака – как и полагается порядочной волновой функции. Сразу становится понятным, что произойдет, если у двух электронов окажутся совпадающими все четыре координаты: определитель, а вместе с ним и функция Y, обратится в ноль. Таким образом, запись волновой функции в виде определителя Слейтера автоматически обеспечивает ее соответствие принципу Паули.

Выводы

Именно этому подходу обязана современная химия такими понятиями, как гибридизация, перекрывание орбиталей, каноническая структура, резонанс. Общая идея, в общем, понятна: для нашей молекулы всякая связь образуется парой электронов с противоположными спинами и описывается взаимодействием двух атомных функций (орбиталей). При этом, правда, сразу возникают вопросы. Во-первых, неясно, какая из атомных орбиталей участвует в каждой из связей. Или все со всеми? Например, в четырехэлектронной системе? Ответ на этот вопрос найден Ю.Б. Румером. Во-вторых, сразу возникла проблема описания бензола. Оказалось, что, записав только одну из возможных конфигураций, мы получаем очень плохое значение энергии. Это, в свою очередь, послужило основой для введения концепции резонанса.

Можно показать, что образующаяся связь тем прочнее, чем больше интеграл перекрывания взаимодействующих орбиталей. Это дало толчок развитию концепции гибридизации, заодно позволив описать направленную валентность.

В общем, на качественном уровне модель работала неплохо, а личное обаяние и популяризаторский талант нобелевского лауреата Л. Полинга способствовало широкому проникновению метода ВС в модельные представления химиков.

Гораздо хуже обстояло дело с вычислительной стороной теории.

Нам приходится строить сразу многоэлектронную волновую функцию, а это очень непросто.

Вот если бы можно было для каждого отдельного электрона нашей многоэлектронной системы записать свое отдельное уравнение, имеющее дело с координатами только одного электрончика… Да, понятно, что в гамильтониане уже двухэлектронной системы присутствует член 1/ r ₁₂, который и мешает разделить переменные, но, может быть, можно как-то договориться, попробовать выделить в этом взаимодействии части, которые относились бы к одному из электронов? В нашем уравнении для молекулы водорода это соответствовало бы представлению 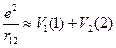, где потенциальная энергия V ₁(1) зависела бы только от координат электрона 1.

Первая попытка такого рассмотрения была предпринята Дж. Хартри.

Метод Хартри

Предположим, что распределение электрона 1 описывается функцией y₁(1), а электрона 2 – функцией y₂(2). Тогда общий гамильтониан можно было бы записать в виде двух одноэлектронных составляющих (и еще энергии отталкивания ядер, которая от координат электронов вообще не зависит):

Обратите внимание: оператор вклада отталкивания электрона 1 от электрона 2 в потенциальную энергию электрона 1 не зависит от координат электрона 2: они целиком остались под интегралом. Поэтому наше уравнение Шредингера, зависевшее от координат двух электронов (и категорически не желавшее решаться) свелось к двум уравнениям:

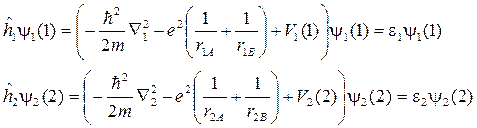
Аналогично, можно рассмотреть систему N электронов, введя потенциал

,

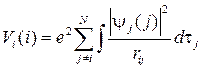описывающий кулоновское взаимодействие i -го электрона с усредненным полем остальных электронов. Такое описание, позволяющее описать каждый электрон многоэлектронной системы своим одноэлектронным уравнением относительно своей одноэлектронной функции, получило название одноэлектронного приближения.

Почему одноэлектронное – понятно. А почему «приближение»? Что здесь, собственно, неточно?

Неверно то, что при рассмотрении электрона с номером i распределение оставшихся электронов предполагается неизменным. Это означает, что электроны движутся независимо друг от друга. На самом деле в нашей, например, двухэлектронной системе поведение электронов не будет независимым, в частности, они будут держаться подальше друг от друга из-за кулоновского отталкивания.

В рассмотрении Хартри предполагалось, что волновая функция системы N независимых электронов может быть представлена произведением

Y = y₁(1) y₂(2) …y _N (N)

а энергия системы будет определяться энергией отдельных электронов

E = e₁ + e₂ + e₃ +…+ e _N.

Остается только подставить и начать считать? Хочется, однако, обратить внимание на одну странность нашего рассмотрения: для того, чтобы записать уравнение для первого электрона, необходимо знать волновые функции всех остальных электронов. Поэтому остальные уравнения уже должны быть решены. Но для того, чтобы записать уравнение для второго электрона, необходимо знать волновые функции всех остальных электронов, в том числе и первого! Кажется мы в тупике.

Именно Хартри придумал, как решать эту задачу. Основная идея проста: а давайте вместо нужных нам функций подставим какие-нибудь (лучше, конечно, правдоподобные). Хартри, например, собирался решать уравнения Шредингера для многоэлектронных атомов, поэтому он в качестве такого стартового приближения предлагал взять функции водородоподобного атома. Используя приближенные функции, построим одноэлектронные уравнения и решим их. Понятно, что поскольку и сами уравнения – лишь приближения к нашим одноэлектронным уравнениям, то и решения их не слишком надежны. Однако мы можем использовать полученные функции для того, чтобы построить новые одноэлектронные уравнения, возможно, более точные. Помните, как мы вычисляли квадратный корень методом Ньютона? Вот и теперь мы будем повторять нашу итерационную процедуру, пока функции, полученные в результате решения уравнений, не совпадут с теми, на основе которых эти уравнения получены. Такой подход получил название метода самосогласованного поля: считается, что электронное распределение каждого электрона уже согласуется с распределением остальных участников собрания.

За эти две идеи – способ разделения N -электронной задачи на N одноэлектронных задач и способ решения полученных уравнений,– Хартри можно просить многое, в том числе и то, что полученные им результаты очень плохо согласовывались с экспериментом. Одна из ошибок нашлась сразу: оказалось, что суммарная энергия системы, вычисленная непосредственно с функцией Y = y₁(1) y₂(2) …y _N (N), не равна сумме энергий отдельных электронов. Действительно, энергия первого электрона включает, в частности, энергию его отталкивания от электрона 2, а энергия второго – энергию его отталкивания от электрона 1, т.е. межэлектронное отталкивание в такой формулировке оказывается учтенным дважды.

Другой недостаток вы должны были обнаружить сразу. Полная волновая функция метода Хартри не удовлетворяет принципу Паули!

Как вы, наверное, уже догадались, вместо простого произведения одноэлектронных функций следует взять определитель Слейтера. Соответствующие уравнения были получены в 1930 г. В.А. Фоком. До сих пор метод Хартри–Фока лежит в основе большинства квантовохимических подходов.

Получающиеся уравнения уже учитывают неразличимость электронов и требования принципа Паули. Остается только их решить. С использованием итерационной процедуры, разумеется. Здесь, правда, опять заминка: опять не делятся переменные, теперь уже связанные с одним-единственным электроном. Вы помните, на похожую проблему мы наталкивались в задаче об атоме водорода. Тогда мы перешли в сферическую систему координат, и решили-таки наши уравнения. Уравнения Хартри-Фока при наличии сферической симметрии решить тоже удается, но только численно. А уж если речь заходит о молекулах, остается лишь вводить новый уровень приближений.

В то же время нельзя не отметить и определенного успеха в наших рассуждениях: мы готовы к тому, чтобы существенно упростить многоэлектронную задачу для молекулы, сведя ее к набору одноэлектронных уравнений, в которых каждый электрон будет описываться своей спин-орбиталью, размазанной, в общем случае, по всей молекуле.

Полную волновую функцию мы будем строить в виде определителя Слейтера из спин-орбиталей y _i, которые можно представить в виде произведения пространственной и спиновой частей: y _i = j _i s _i. Для молекулы с четным числом электронов 2 N, где все электроны спарены (а огромное большинство устойчивых молекул имеет такую, как говорят, замкнутую оболочку) это может быть записано в виде:

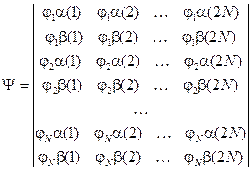
Такой определитель предполагает, что все наши МО двукратно заняты.

Ну, а необходимое приближение у нас уже почти в руках – это упоминавшийся ранее метод МО ЛКАО.

Каждая МО строится как ЛКАО: 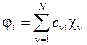. Такой выбор хорош по двум причинам: во-первых, мы получим неплохое описание, по крайней мере, в окрестностях атома, а во-вторых, такое представление приведет нас в уже знакомую гавань вариационного метода: базис c_n остается неизменным, но коэффициенты с _{n i} можно будет подобрать наилучшим образом. Можно показать, что для молекул с закрытой оболочкой (при наличии неспаренных электронов все сильно запутывается) это приводит к уравнениям Рутаана:

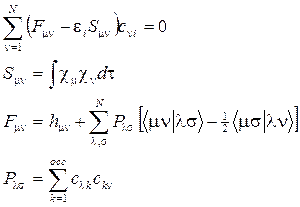
– одноэлектронные энергии. Одно из их замечательных свойств доказывается в теореме Купманса.

Date: 2015-07-10; view: 3008; Нарушение авторских прав