
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методические рекомендации к решению контрольной работы
|
|
Б) АВ, ВА
В) 3A+2B.
| вариант | k | l | m | n | p | q | r | s |
Задание 2. Для матриц А= 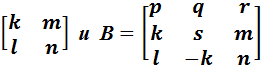 найти
найти
А) 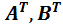
Б) определители матриц А, В.
| вариант | k | l | m | n | p | q | r | s |
Задание 3. Для матриц А= 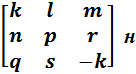 айти обратную матрицу, сделать проверку.
айти обратную матрицу, сделать проверку.
| вариант | k | l | m | n | p | q | r | s |
Задание 4. Найти неизвестную матрицу Х из следующего уравнения. Ответ проверить подстановкой в уравнение и умножением
1. 
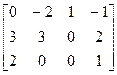
2. 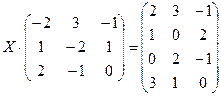
3. 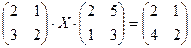
4. 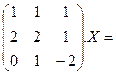
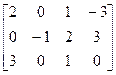
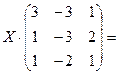
5. 
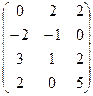
6. 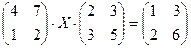
7. 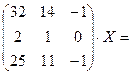
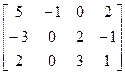
8. 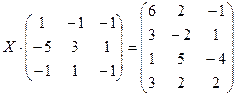
9. 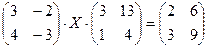
10. 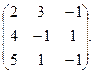
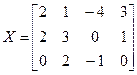
Задание 5. Решить систему линейных уравнений
А) методом Гаусса,
Б) матричным способом,
В)используя правило Крамера.
1. 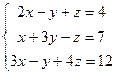
2. 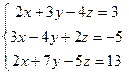
3. 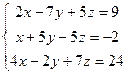
4. 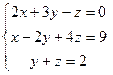
5. 
6. 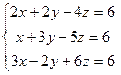
7. 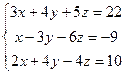
8. 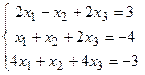
9. 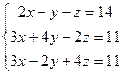
10. 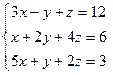
Задание 6.Построить прямую 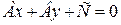 . Определить ее угловой коэффициент. Составить уравнения нескольких прямых, параллельных ей. Записать уравнение прямой, перпендикулярной к данной и проходящей через начало координат. Коэффициенты А, В, С заданы в таблице:
. Определить ее угловой коэффициент. Составить уравнения нескольких прямых, параллельных ей. Записать уравнение прямой, перпендикулярной к данной и проходящей через начало координат. Коэффициенты А, В, С заданы в таблице:
| Вариант | А | В | С |
| -2 | |||
| -6 | -2 | -10 | |
| -12 | |||
| -3 | |||
| -6 | -4 | ||
| -15 | |||
| -9 | |||
| -15 | |||
| -20 |
Задание 7. В таблице приведены данные об исполнении баланса. Используя модель Леонтьева многоотраслевой экономики, вычислить необходимый объем валового выпуска каждой отрасли, если конечный выпуск энергетической отрасли увеличится вдвое, а машиностроительной сохранится на прежнем уровне.
| Вариант 1 | |||||||||||
| Отрасль | Потребление | Конечный продукт | Валовой продукт | ||||||||
| Энергетическая | |||||||||||
| Машиностроение | |||||||||||
| Вариант 2 | |||||||||||
| Отрасль | Потребление | Конечный продукт | Валовой продукт | ||||||||
| Энергетическая | |||||||||||
| Машиностроение | |||||||||||
| Вариант 3 | |||||||||||
| Отрасль | Потребление | Конечный продукт | Валовой продукт | ||||||||
| Энергетическая | |||||||||||
| Машиностроение | |||||||||||
| Вариант 4 | |||||||||||
| Отрасль | Потребление | Конечный продукт | Валовой продукт | ||||||||
| Энергетическая | |||||||||||
| Машиностроение | |||||||||||
| Вариант 5 | |||||||||||
| Отрасль | Потребление | Конечный продукт | Валовой продукт | ||||||||
| Энергетическая | |||||||||||
| Машиностроение | |||||||||||
| Вариант 6 | |||||||||||
| Отрасль | Потребление | Конечный продукт | Валовой продукт | ||||||||
| Энергетическая | |||||||||||
| Машиностроение | |||||||||||
| Вариант 7 | |||||||||||
| Отрасль | Потребление | Конечный продукт | Валовой продукт | ||||||||
| Энергетическая | |||||||||||
| Машиностроение | |||||||||||
| Вариант 8 | |||||||||||
| Отрасль | Потребление | Конечный продукт | Валовой продукт | ||||||||
| Энергетическая | |||||||||||
| Машиностроение | |||||||||||
| Вариант 9 | |||||||||||
| Отрасль | Потребление | Конечный продукт | Валовой продукт | ||||||||
| Энергетическая | |||||||||||
| Машиностроение | |||||||||||
| Вариант 10 | |||||||||||
| № | Отрасль | Потребление | Конечный продукт | Валовой продукт | |||||||
| Энергетическая | |||||||||||
| Машиностроение | |||||||||||
ВОПРОСЫ К ЭКЗАМЕНУ
1. Системы линейных уравнений (СЛУ). Их решения. Типы СЛУ. Примеры
2. Равносильные системы уравнений. Элементарные преобразования СЛУ.
3. Матрица и расширенная матрица СЛУ. Примеры.
4. Ступенчатая матрица. Примеры.
5. Приведение матрицы к ступенчатому виду.
6. Метод Гаусса решения СЛУ. Общая схема
7. Сложение матриц и его свойства. Нулевая матрица. Примеры.
8. Умножение матрицы на число и его свойства. Примеры.
9. Умножение матриц и его свойства. Единичная матрица. Примеры.
10. Обратная матрица (определение и свойства).
11. Нахождение обратной матрицы с помощью элементарных преобразований. Пример.
12. Решение систем линейных уравнений в матричном виде. Пример.
13. Определители второго порядка. Примеры.
14. Определители третьего порядка. Примеры.
15. Определители n-го порядка. Примеры.
16. Свойства определителей. Примеры.
17. Миноры и алгебраические дополнения. Примеры.
18. Разложение определителя по элементам строки (столбца). Примеры.
19. Обратная матрица через алгебраические дополнения. Примеры.
20. Наличие обратной матрицы.
21. Определитель произведения двух матриц.
22. Правило Крамера для решения СЛУ.
23. Линейная модель Леонтьева многоотраслевой экономики. Примеры.
24. Решение СЛАУ методом обратной матрицы.
25. Метод последовательного исключения неизвестных. Метод Гаусса.
26. Метод Крамера. Достоинства и недостатки различных методов решения СЛАУ.
27. Общее уравнение прямой линии на плоскости.
28. Построение прямой. Уравнение прямой в отрезках.
29. Уравнение прямой с угловым коэффициентом.
30. Поведение прямой на графике в зависимости от параметров ее уравнения.
31. Частные случаи положения прямых.
32. Уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом. Уравнение пучка прямых.
33. Уравнение прямой, проходящей через две данные точки.
34. Угол между прямыми. Условие параллельности прямых. Условие перпендикулярности прямых.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К РЕШЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Задание 4. Решить матричное уравнение, выполнить проверку
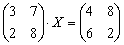
Решение: Уравнение уже имеет вид  , поэтому никаких предварительных действий проводить не нужно.
, поэтому никаких предварительных действий проводить не нужно.
Для разрешения уравнения относительно 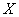 умножим обе его части на
умножим обе его части на 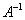 слева:
слева:
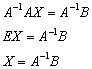
Да-да, прямо так и пишем при оформлении решения. Хотя можно ограничиться единственной фразой: «Решение ищем в виде 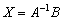 » – без всяких пояснений и вывода формулы
» – без всяких пояснений и вывода формулы 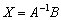 .
.
Из условия известны матрицы 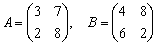 , однако, обратной матрицы
, однако, обратной матрицы 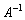 мы не знаем. Придётся её найти:
мы не знаем. Придётся её найти:
Обратную матрицу найдем по формуле:
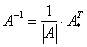 , где
, где 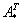 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы 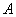 .
.
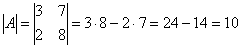
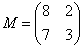 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы 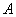 .
.
 – матрица алгебраических дополнений.
– матрица алгебраических дополнений.
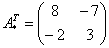 – транспонированная матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.
Таким образом, обратная матрица:
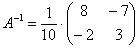
На финише проводим матричное умножение и получаем решение:
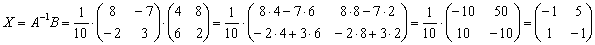
Ответ: 
Проверка: Подставим найденное значение 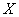 в левую часть исходного уравнения:
в левую часть исходного уравнения:
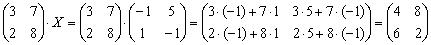
Получена правая часть исходного уравнения. Таким образом, решение найдено правильно.
Задание 5. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Решение:
Решим систему матричным способом, для этого вычислим обратную матрицу 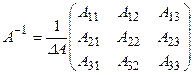 , где
, где 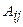 - алгебраические дополнения к элементам матрицы.
- алгебраические дополнения к элементам матрицы.
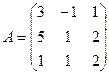
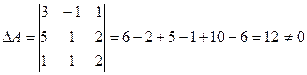 - матрица невырожденная.
- матрица невырожденная.
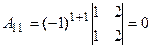

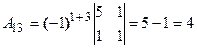
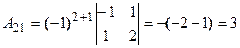
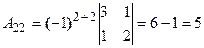
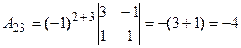
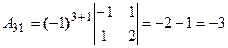
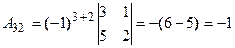
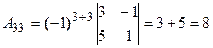
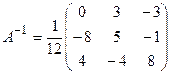
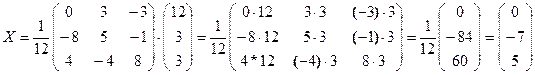
Решим систему методом Крамера. Главный определитель системы:
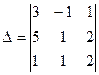 . Разложим определитель по элементам первой строки, пользуясь формулой
. Разложим определитель по элементам первой строки, пользуясь формулой 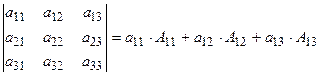 .
.
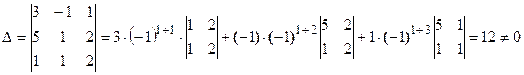
Запишем и вычислим вспомогательные определители
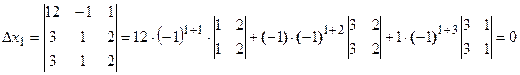
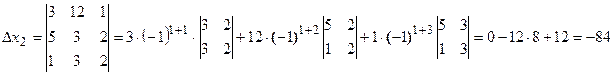
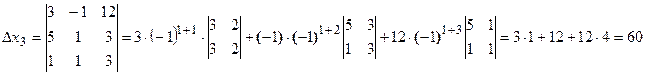 Тогда
Тогда 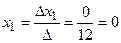 ;
; 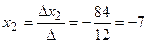 ;
; 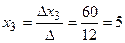
Ответ: 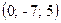
Решим систему методом Гаусса, для этого составим расширенную матрицу системы и упростим ее приведением к треугольному виду.
 ~
~ 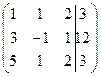 ~
~ 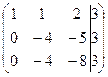 ~
~ 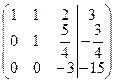
Таким образом, система равносильна системе
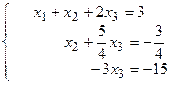
Находим 
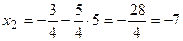
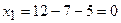
Ответ: 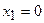 ,
, 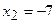 ,
, 
При решении всеми методами одной и той же системы, мы получим один
ответ.
Задание 6. Построить прямую 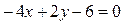 . Определить ее угловой коэффициент. Составить уравнения нескольких прямых, параллельных ей. Записать уравнение прямой, перпендикулярной к данной и проходящей через начало координат.
. Определить ее угловой коэффициент. Составить уравнения нескольких прямых, параллельных ей. Записать уравнение прямой, перпендикулярной к данной и проходящей через начало координат.
Преобразуем заданное уравнение – решим его относительно y, получим уравнение: 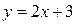 . Отсюда угловой коэффициент прямой равен: - А/В = -(-4)/2 = 2.
. Отсюда угловой коэффициент прямой равен: - А/В = -(-4)/2 = 2.
Для построения прямой нужно знать координаты двух точек, удовлетворяющих ее уравнению. Задавая 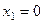 , получим
, получим 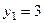 . Задавая
. Задавая 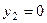 , получим
, получим 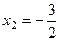 . Значит, прямая проходит через точки А (0; 3) и В (-3/2; 0) (рис. 1). Координаты точек, по которым строится график прямой, удобно записывать в таблицу:
. Значит, прямая проходит через точки А (0; 3) и В (-3/2; 0) (рис. 1). Координаты точек, по которым строится график прямой, удобно записывать в таблицу:

| x | 3/2 | |
| y |
Рис. 1
Параллельные прямые имеют одинаковый угловой коэффициент, т.е. для заданной прямой параллельными, например, будут прямые:
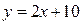 ,
, 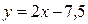 ,
, 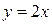 и т.д.
и т.д.
Произведение угловых коэффициентов параллельных прямых равно –1. Поэтому угловой коэффициент прямых, перпендикулярных заданной прямой, будет равен –1/2. Если прямая проходит через начало координат, то свободный член в уравнении такой прямой равен 0.
Тогда уравнение прямой, перпендикулярной к данной и проходящей через начало координат, будет иметь вид: 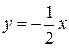 .
.
Задание 7. В таблице приведены данные об исполнении баланса. Используя модель Леонтьева многоотраслевой экономики, вычислить необходимый объем валового выпуска каждой отрасли, если конечный выпуск энергетической отрасли увеличится вдвое, а машиностроительной сохранится на прежнем уровне.
| № | Отрасль | Потребление | Конечный продукт | Валовой продукт | ||
| 1. | Энергетическая | |||||
| 2. | Машиностроение | |||||
Date: 2015-07-10; view: 421; Нарушение авторских прав