
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Прогнозирование
|
|
Коэффициент корреляции.
Диаграмма рассеяния.
Регрессионный анализ.
Проверка надежности регрессионной модели.
Прогнозирование.
Тремя основными целями анализа двумерных данных, представленных парами (Х, У), являются: (1) описание и понимание взаимосвязи, (2) прогнозирование и предсказание нового наблюдения и (3) корректировка и управление процессом.
Корреляционный анализ позволяет сделать вывод о силе взаимосвязи, а регрессионный анализ используется для прогнозирования одной переменной на основании другой (как правило, У на основании X).
Двумерные данные анализируют с использованием диаграммы рассеяния в координатах У и X, которая дает визуальное представление о взаимосвязи в данных. Корреляция, или точнее линейный коэффициент корреляции ( г ), представляет собой безразмерное (не имеющее единиц измерения) число в диапазоне от -1 до 1, которое характеризует силу взаимосвязи. Равенство коэффициента корреляции 1 свидетельствует об идеальной взаимосвязи в виде прямой линии с наклоном вверх. Равенство коэффициента корреляции -1 свидетельствует об идеальной взаимосвязи в виде наклоненной вниз (отрицательно) прямой линии. Коэффициент корреляции говорит о том, насколько близко к этой наклоненной прямой линии расположены точки диаграммы, однако он не характеризует крутизну наклона этой линии. Формула вычисления коэффициента корреляции для тех, кто умеет пользоваться Excel имеет следующий вид:
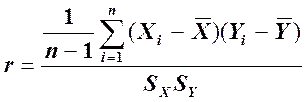 .
.
Ковариация X и У представляет собой числитель в формуле для коэффициента корреляции. Поскольку единицы измерения ковариации трудно интерпретировать, удобнее работать с коэффициентом корреляции.
Корреляцию нельзя рассматривать как причинную обусловленность. Коэффициент корреляции характеризует связь между числами, но не объясняет ее. Корреляция может быть вызвана тем, что переменная X влияет на У, или тем, что переменная У влияет на X. Кроме того, корреляция может быть вызвана также тем, что на X и У влияет некий скрытый "третий фактор", что создает впечатление связи между X и У. Термином ложная корреляция обозначают высокую корреляцию, которая возникает благодаря действию некоторого третьего фактора.
При анализе двумерной диаграммы рассеяния можно обнаружить различные взаимосвязи. Простейшей, с точки зрения анализа, является линейная взаимосвязь, которая выражается в том, что точки на диаграмме рассеяния с постоянным разбросом группируются случайным образом вдоль прямой линии. Диаграмма свидетельствует об отсутствии взаимосвязи, если точки размещены случайно и при перемещении слева направо невозможно обнаружить какой-либо уклон (ни вверх, ни вниз). Двумерная диаграмма рассеяния характеризуется нелинейной взаимосвязью, если точки на ней группируются вдоль кривой, а не прямой линии. Поскольку количество видов кривых практически безгранично, анализ нелинейной взаимосвязи оказывается намного сложнее, однако взаимосвязь можно приблизить к линейной, применив к данным соответствующее преобразование. Проблема неравной вариации возникает тогда, когда при перемещении по горизонтали на диаграмме рассеяния вариация точек по вертикали сильно меняется. Неравная вариация приводит к снижению надежности коэффициента корреляции и регрессионного анализа. Проблему неравной вариации можно решить с помощью соответствующих преобразований данных или с помощью, так называемой взвешенной регрессии. Проблема кластеринга (разделение совокупности на группы более однородных объектов) возникает в случае образования на диаграмме рассеяния отдельных, ярко выраженных групп точек; втаких случаях каждую группу следует анализировать отдельно. Некоторая точка данных является выбросом (резко отклоняющимся значением), если она не соответствует взаимосвязи между остальными данными; резко отклоняющиеся значения могут исказить статистические характеристики двумерной совокупности данных.
Регрессионный анализ заключается в прогнозировании одной переменной на основании другой. Линейный регрессионный анализ прогнозирует значение одной переменной на основании другой с помощью прямой линии. Наклон этой линии, выражается в единицах измерения У на одну единицу X и характеризует крутизну подъема или спуска (если b отрицательное) линии. Сдвиг, a, равен значению, которое принимает У при X, равном 0. Уравнение прямой линии имеет следующий вид:
Y = Сдвиг + (Наклон)(Х) = а + bХ.
Линия наименьших квадратов характеризуется наименьшей из всех возможных линий суммой возведенных в квадрат ошибок прогнозирования по вертикали и используется как лучшая линия прогнозирования, основанная на данных. Наклон этой линии, b, называют также коэффициентом регрессии У по X, а сдвиг а (отрезок отсекаемый на оси У) называют также постоянным членом регрессии. Ниже приведены уравнения для наклона и сдвига, соответствующие линии наименьших квадратов.
Наклон равен:  .
.
Сдвиг равен: 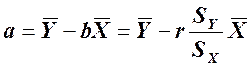 .
.
Формула для линии наименьших квадратов имеет следующий вид:
Прогнозируемое значение У равно:
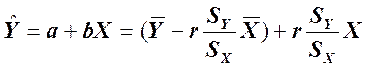 .
.
Прогнозируемое значение для У при заданном значении X определяется путем подстановки этого значения X в уравнение для линии наименьших квадратов. Каждая из точек данных характеризуется остатком – ошибкой прогнозирования, указывающей, насколько выше или ниже линии находится точка.
Существуют две меры соответствия линии наименьших квадратов имеющимся данным. Стандартная ошибка оценки (или предсказания), которую обозначают 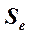 , приблизительно указывает величину ошибок прогнозирования (остатков) для имеющихся данных в тех же единицах, в которых измерена и переменная У. Соответствующие формулы приведены ниже.
, приблизительно указывает величину ошибок прогнозирования (остатков) для имеющихся данных в тех же единицах, в которых измерена и переменная У. Соответствующие формулы приведены ниже.
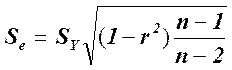 (для вычисления)
(для вычисления)
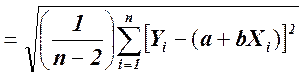 (для интерпретации).
(для интерпретации).
Значение 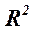 , часто называемое коэффициентом детерминации, говорит о том, какой процент вариации У объясняется поведением X.
, часто называемое коэффициентом детерминации, говорит о том, какой процент вариации У объясняется поведением X.
Доверительные интервалы и проверка гипотез для коэффициента регрессии связаны с определенными предположениями относительно анализируемой совокупности данных, которые должны гарантировать, что она состоит из независимых наблюдений, характеризующихся линейной взаимосвязью с равной вариацией и приблизительно нормально распределенной случайностью. Во-первых, эти данные должны представлять собой произвольную выборку из интересующей нас генеральной совокупности. Во-вторых, линейная модель указывает, что наблюдаемое значение У определяется взаимосвязью в генеральной совокупности плюс случайная ошибка, имеющая нормальное распределение. Существуют параметры генеральной совокупности, соответствующие наклону и сдвигу линии наименьших квадратов, построенной на данных выборки:
Y = ( α + β Х)+ ε =
= (Взаимосвязь в генеральной совокупности) + случайность.
где ε имеет нормальное распределение со средним значением, равным 0, и постоянным стандартным отклонением σ.
Статистические выводы (использование доверительных интервалов и проверки статистических гипотез) относительно коэффициентов линии наименьших квадратов основываются, как обычно, на их стандартных ошибках и значениях из t -таблицы для п - 2 степеней свободы. Стандартная ошибка коэффициента наклона,  , указывает приблизительную величину отклонения оценки наклона, b (коэффициент регрессии, вычисленный на основе данных выборки), от наклона в генеральной совокупности, β, вызванного случайным характером выборки. Стандартная ошибка сдвига,
, указывает приблизительную величину отклонения оценки наклона, b (коэффициент регрессии, вычисленный на основе данных выборки), от наклона в генеральной совокупности, β, вызванного случайным характером выборки. Стандартная ошибка сдвига, 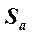 , указывает приблизительно, насколько далеко оценка сдвига а отстоит от истинного сдвига α в генеральной совокупности. Соответствующие формулы выглядят следующим образом:
, указывает приблизительно, насколько далеко оценка сдвига а отстоит от истинного сдвига α в генеральной совокупности. Соответствующие формулы выглядят следующим образом:
стандартная ошибка коэффициента регрессии b:
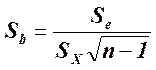
стандартная ошибка сдвига:
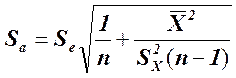 .
.
Доверительный интервал для наклона в генеральной совокупности, β:
от  до
до 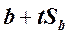 .
.
Доверительный интервал для сдвига в генеральной совокупности, α:
от 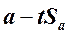 до
до 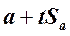 .
.
Один из способов проверки, является ли обнаруженная взаимосвязь между X и У реальной или это просто случайное совпадение, заключается в сравнении β с заданным значением β0 = 0. О значимой связи можно говорить в том случае, если 0 не попадает в доверительный интервал, базирующийся на b и Sb, или если абсолютное значение t = b/Sb превосходит соответствующее t -значение в t - таблице.
t – таблица (t - критерий Стьюдента)
| Доверительный интервал | |||||||
| Двухсторонний | 80% | 90% | 95% | 98% | 99% | 99,8% | 99,9% |
| Односторонний | 90% | 95% | 97,5% | 99% | 99,5% | 99,9% | 99,95% |
| Уровень значимости проверки гипотезы | |||||||
| Двухсторонний тест | 0,20 | 0,10 | 0,05 | 0,02 | 0,01 | 0,002 | 0,001 |
| Односторонний тест | 0,10 | 0,05 | 0,025 | 0,01 | 0,005 | 0,001 | 0,0005 |
| В целом: степени свободы | Критические значения t | ||||||
| 3,078 | 6,314 | 12,706 | 31,821 | 63,657 | 318,309 | 636,619 | |
| 1,886 | 2,920 | 4,303 | 6,965 | 9,925 | 22,327 | 31,599 | |
| 1,638 | 2,353 | 3,182 | 4,541 | 5,841 | 10,215 | 12,924 | |
| 1,533 | 2,132 | 2,776 | 3,747 | 4,604 | 7,173 | 8,610 | |
| 1,476 | 2,015 | 2,571 | 3,365 | 4,032 | 5,893 | 6,869 | |
| 1,440 | 1,943 | 2,447 | 3,143 | 3,707 | 5,208 | 5,959 | |
| 1,415 | 1,895 | 2,365 | 2,998 | 3,499 | 4,785 | 5,408 | |
| 1,397 | 1,860 | 2,306 | 2,896 | 3,355 | 4,505 | 5,041 | |
| 1,383 | 1,833 | 2,262 | 2,821 | 3,250 | 4,297 | 4,781 | |
| 1,372 | 1,812 | 2,228 | 2,764 | 3,169 | 4,144 | 4,587 | |
| 1,363 | 1,796 | 2,201 | 2,718 | 3,106 | 4,025 | 4,437 | |
| 1,356 | 1,782 | 2,179 | 2,681 | 3,055 | 3,930 | 4,318 | |
| 1,350 | 1,771 | 2,160 | 2,650 | 3,012 | 3,852 | 4,221 | |
| 1,345 | 1,761 | 2,145 | 2,624 | 2,977 | 3,787 | 4,140 | |
| 1,341 | 1,753 | 2,131 | 2,602 | 2,947 | 3,733 | 4,073 | |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| 1,304 | 1,686 | 2,024 | 2,429 | 2,712 | 3,319 | 3,566 | |
| 1,304 | 1,685 | 1,023 | 2,426 | 2,708 | 3,313 | 3,558 | |
| Бесконечность | 1,282 | 1,645 | 1,960 | 2,326 | 2,576 | 3,090 | 3,291 |
Эта проверка эквивалентна проверке значимости коэффициента корреляции и означает, по сути, то же самое, что и F -тест для случая, когда уравнение содержит только одну переменную X. Разумеется, любой из коэффициентов (a или b ) можно сравнить с любым подходящим заданным значением, воспользовавшись одно- или двусторонней проверкой (в зависимости от конкретных обстоятельств) и с использованием тех же методов проверки, что были рассмотрены для среднего генеральной совокупности.
Для прогнозирования среднего значения нового наблюдения У при условии, что X = Х0 (где Х0 – интересующий исследователя параметр X, который еще ни разу не встречался в обыденной практике), неопределенность прогноза оценивают с помощью стандартной ошибки прогноза S(прогнозируемое Y/X0) , которая также имеет п – 2 степеней свободы. Это позволяет построить доверительные интервалы и проверить гипотезы для нового наблюдения:
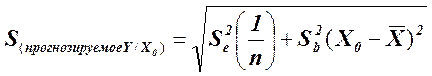
Доверительный интервал для прогнозируемого среднего значения У при заданном значении Х0 имеет следующий вид:
от 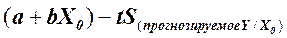
до 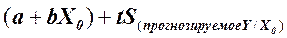
Date: 2015-07-10; view: 3050; Нарушение авторских прав