Изображение комплексных чисел

Комплексные числа записываются в виде: a+ bi. Здесь a и b – действительные числа, а i – мнимая единица, т.e. i ² = –1. Число a называется абсциссой, a b – ординатой комплексного числа a+ bi. Комплексное число 0 + bi называется чисто мнимым числом. Запись bi означает то же самое, что и 0 + bi.

Модулем комплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Сопряжённые комплексные числа имеют одинаковый модуль

Рассмотрим на плоскости декартову прямоугольную систему координат xOy. Каждому комплексному числу z = a + bi можно сопоставить точку с координатами (a;b), и наоборот, каждой точке с координатами (c;d) можно сопоставить комплексное число w = c + di. Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью.

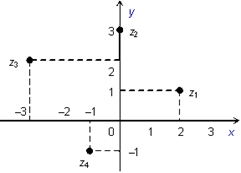
Пример. Изобразим на комплексной плоскости числа

Z₁ = 2 + i; z₂ = 3i; z₃ = -3 + 2i; z₄ = -1 – i.

Решение:

Арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d) i, а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc) i (здесь как раз используется, что i ² = –1). Число 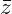= a – bi называется комплексно-сопряженным к z = a + bi. Равенство z · 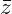= a ² + b ² позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:

.

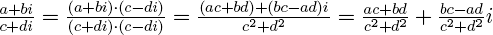Например,

Самостоятельная работа

1 вариант	2 вариант	Количество баллов
№ 1. Изобразите на плоскости заданные комплексные числа:
Z1 = 4i	Z 1= -5i
Z2 = 3 + i	Z 2= 4 + i
Z 3= - 4 +3i	Z3 = -7 + 2i
Z 4= - 2 -5i	Z 4= -3 – 6i
№ 2. Вычислите модули заданных комплексных чисел
Z5 = 3 + 4i	Z5 = 8 + 6i
№ 3. Произведите сложение и вычитание комплексных чисел:
А) (3 + 5 i) + (7 – 2 i). б) (6 + 2 i) + (5 + 3 i). в) (– 2 + 3 i) + (7 – 2 i). г) (5 – 4 i) + (6 + 2 i).	(3 – 2 i) + (5 + i). (4 + 2 i) + (– 3 + 2 i). (– 5 + 2 i) + (5 + 2 i). (– 3 – 5 i) + (7 – 2 i).
№ 4. Произведите умножение комплексных чисел:
А) (2 + 3 i)(5 – 7 i). б) (6 + 4 i)(5 + 2 i). в) 11) (3 – 2 i)(7 – i). г) (– 2 + 3 i)(3 + 5 i).	(1 – i)(1 + i). (3 + 2 i)(1 + i). (6 + 4 i)3 i. (2 – 3i)(– 5i).	2 2 2 2
№ 5. Выполните действия:
А) (3 + 5 i)2. Б) (2 – 7 i)2. в) (6 + i)2. г) (1 – 5 i)2.	А) (3 + 2 i)2. б) (3 – 2 i)2. в) (4 + 2 i)2. г) (5 – i)2.
№ 6. Выполните действия:
А) (3 + 2 i)(3 – 2 i). б) (5 + i)(5 – i). в) (1 – 3 i)(1 + 3 i).	а) (7 – 6 i)(7 + 6 i). б) (4 + i)(4 – i). в) (1 – 5 i)(1 + 5 i).
№ 7. Решите уравнения:
а) x 2 – 4 x + 13 = 0. б) x 2 + 3 x + 4	а) 2,5 x 2 + x + 1 = 0. б) 4 x 2 – 20 x + 26 = 0.	3 3
№ 8. На рисунке показано графическое изображение комплексных чисел. Перерисуйте рисунок в тетрадь. Обозначьте комплексные числа как z1, z2, zЗ. Запишите соответствующие аналитические формы.