Алгоритм шифрования Эль Гамаль

Асимметричная схема Эль Гамаль, предложенная автором (El Gamal), использует операцию возведения в степень по модулю простого числа. При этом трудноразрешимой задачей для злоумышленника является отыскание не числа, которое возведено в степень, а то, в какую степень возведено известное число. Эта задача носит название проблемы дискретного логарифма.

На этапе выработки ключей:

1. Выбирается произвольное (правда достаточно большое) простое число р.

2. Для этого простого числа определяется любой образующий элемент (англ. primitive root) – т. е. такое число а, при многократном возведении которого в степень по модулю р (а¹ mod p, a² mod p, …), будут перебираться (в произвольном порядке, но обязательно по одному разу) все числа от 1 до (p-1) включительно.

3. Генерируется произвольное случайное число х (0<х<p) – это и есть

закрытый ключ.

4. Вычисляется значение b = a^x mod p – комбинация (a, p, b) представляет собой открытый ключ получателя.

На этапе шифрования:

1. Отправитель генерирует произвольное случайное число y (0<y<p).

2. Помещает в начале шифрограммы число (a^y mod p).

3. Вычисляет величину k = (b^y mod p) = ((a^x mod p)^y mod p).

4. Используя некоторую, заранее оговоренную в данной реализации, часть k в качестве симметричного ключа для любого блочного шифра шифрует отправляемое сообщение.

5. Надежно стирает числа y и k из оперативной памяти и других мест, куда они могли случайно попасть.

На этапе дешифрования:

1. По приходу зашифрованного сообщения получатель отделяет от пакета величину (a^y mod p) и вычисляет на ее основе ((a^y mod p)^x mod p) – математика доказывает, что полученное число будет равно тому самому k, которое вычислил отправитель, так как в данной формуле операнды x и y можно менять местами.

2. Выделив из k туже самую часть, что и отправитель, получатель дешифрует весь идущий далее пакет симметричным алгоритмом.

Схема алгоритма Эль Гамаль приведена на рис. 3.2.

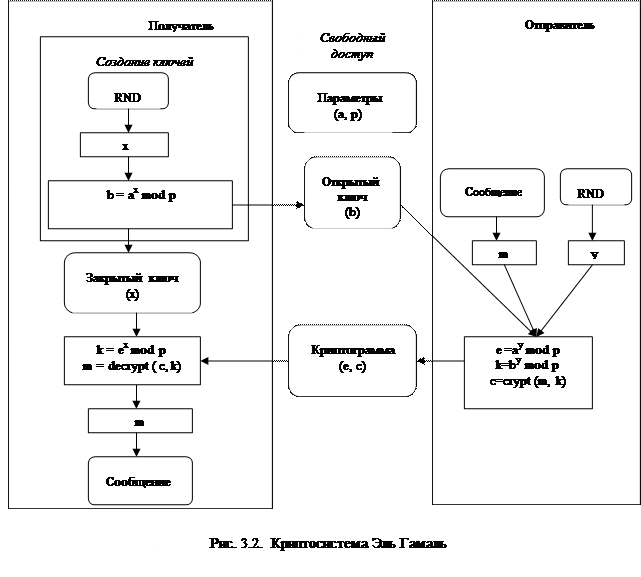
Проблема дискретного логарифма состоит в том, что, зная основание степени и получившийся после возведения результат по модулю простого числа, невозможно за

обозримое время определить, в какую именно степень было возведено основание. В схеме Эль Гамаль потенциальный злоумышленник может получить значения a, p, (a^x mod p) и (a^y mod p). Однако из-за сложности определения чисел х и y "в чистом виде" у него не оказывается возможности вычислить значение k = (a^xy mod p), которое так необходимо для прочтения шифровки.

По криптостойкости с схеме Эль Гамаль 512-битное число p приравнивается к 56-битному симметричному ключу, размер которого в настоящее время недостаточен для надежного шифрования. Поэтому на практике применяются р длиной в 768, 1024 и 1536 бит.

Пример 3. В качестве простого числа, порождающего циклическую группу, выберем р = 11, за образующий элемент примем число а = 7 (при возведении 7 в степень 1, 2, 3 и т. д. по модулю 11 последовательно проходят все 10 значений [7, 5, 2, 3, 10, 4, 6, 9, 8, 1]). Секретным ключом х выберем 6, параметр b принимает значение b = (a^x mod p) = (7⁶ mod 11) = 4. В целом ключ принимает вид (а = 7, р = 11, b = 4).

Предположим, что некий абонент хочет передать сообщение. Он выбрал случайное число, не превосходящее р, например, у = 9. В начало шифрограммы помещается число (a^y mod p) = 7⁹ mod 11) = 8. Кроме того, на основе у и открытого ключа отправитель вычисляет k = b^y mod p = 4⁹ mod 11 = 3. Выбрав значение 3 или какие-либо его биты в качестве симметричного ключа, отправитель шифрует передаваемые данные и стирает величины 9 и 3 со своих накопителей.

Получатель по приходу пакета для вычисления k = (a^y mod p)^x mod p возводит число 8 из заголовка шифрограммы в степень секретного ключа и получает k = 8⁶ mod 11 = 3 – то же самое значение, которое использовал отправитель, шифруя собственно данные.

Date: 2015-06-11; view: 1349; Нарушение авторских прав