
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Перестановочные шифры
|
|
Шифр, преобразования из которого изменяют только порядок следования символов исходного текста, но не изменяют их самих, называется шифром перестановки (ШП). Рассмотрим преобразование из ШП, предназначенное для шифрования сообщения длиной n символов. Его можно представить с помощью таблицы
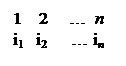

где i1 – номер места шифротекста, на которое попадает первая буква исходного сообщения при выбранном преобразовании, i2 – номер места для второй буквы и т. д.
В верхней строке таблицы выписаны по порядку числа от 1 до n, а в нижней те же числа, но в произвольном порядке. Такая таблица называется подстановкой степени n.
Зная подстановку, задающую преобразование, можно осуществить как шифрование, так и расшифрование текста. Например, если для преобразования используется подстановка

1 2 3 4 5 6
5 2 3 1 4 6
и в соответствии с ней зашифровывается слово МОСКВА, то получится КОСВМА.
Попробуйте расшифровать сообщение НЧЕИУК, полученное в результате преобразования с помощью указанной выше подстановки.
Зная метод математической индукции, легко убедиться в том, что существует n! (n факториал) вариантов заполнения нижней строки таблицы (1). Таким образом, число различных преобразований шифра перестановки, предназначенного для зашифрования сообщений длины n, меньше либо равно n!. (заметим, что в это число входит и вариант преобразования, оставляющий все символы на своих местах!).
С увеличением числа n значение n! факториал растет очень быстро:
Таблица 1.1 – Значения N! для первых 10 натуральных чисел
| n | ||||||||||
| n! |
Примером ШП, предназначенного для зашифрования сообщений длины n, является шифр, в котором в качестве множества ключей взято множество всех подстановок степени n, а соответствующие им преобразования шифра задаются, как было описано выше. Число ключей такого шифра равно n!
Для использования на практике такой шифр неудобен, так как при больших значениях n приходится работать с длинными таблицами.
Широкое распространение получили фигуры перестановки, использующие некоторую геометрическую фигуру. Преобразования из этого шифра состоят в том, что в фигуру исходный текст вписывается по ходу одного "маршрута", а затем по ходу другого выписывается с нее. Такой шифр называется маршрутнойперестановкой. Например, можно вписывать исходное сообщение в прямоугольную таблицу, выбрав такой маршрут: по горизонтали, начиная с левого верхнего поочередно слева направо и справа налево. Выписывать же сообщение будем по другому маршруту: по вертикали, начиная с верхнего правого угла и двигаясь поочередно сверху вниз и снизу вверх.
Зашифруем, например, указанным способом фразу:
ПРИМЕРМАРШРУТНОЙПЕРЕСТАНОВКИ
используя прямоугольник размера 4´7
| П | Р | И | М | Е | Р | М |
| Н | Т | У | Р | Ш | Р | А |
| О | Й | П | Е | Р | Е | С |
| И | К | В | О | Н | А | Т |
Зашифрованная фраза выглядит так:
МАСТЕРРЕШРНОЕРМИУПВКЙТРПНОИ
Теоретически маршруты могут быть значительно более изощренными, однако запутанность маршрутов усложняет использование таких шифров.
Для использования шифра, называемого поворотной решеткой, изготавливается трафарет из прямоугольного листа клетчатой бумаги размера 2m´2k клеток. В трафарете вырезано m´k клеток так, что при наложении его на лист чистой бумаги того же размера четырьмя возможными способами его вырезы полностью покрывают всю площадь листа.
Буквы сообщения последовательно вписываются в вырезы трафарета (по строкам, в каждой строке слева направо) при каждом из четырех его возможных положений в заранее установленном порядке.
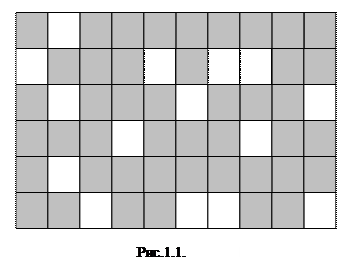
Пример шифрования. Пусть в качестве ключа используется решетка 6´10, приведенная на рис. 1. 1.
Зашифруем с ее помощью текст
ШИФРРЕШЕТКАЯВЛЯЕТСЯ ЧАСТНЫМЛУЧАЕМШИФРАМАРШРУТНОЙ ПЕРЕСТАНОВКИ
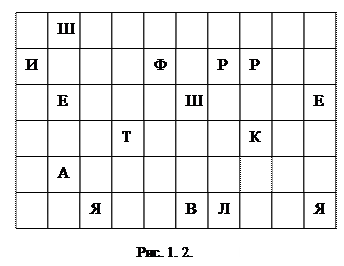
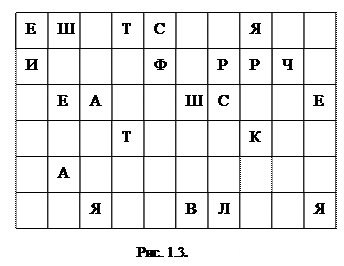
Наложив решетку на лист бумаги, вписываем первые 15 (по числу вырезов) букв сообщения ШИФРРЕШЕТКАЯВЛЯ….. Сняв решетку, мы увидим текст, представленный на рис. 1. 2. Поворачиваем решетку на 180°. В окошечках появятся новые, еще не заполненные клетки. Вписываем в них следующие 15 букв. Получится запись, приведенная на рис. 1. 3. Затем поворачиваем решетку на другую сторону и зашифровываем остаток текста аналогичным образом (рис. 1.4, 1.5).

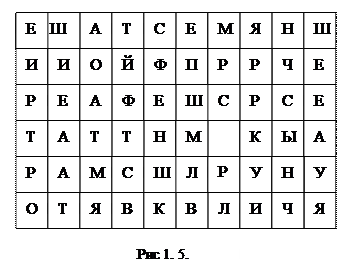
Получатель сообщения, имеющий точно такую же решетку, без труда прочтет исходный текст, наложив решетку на шифротекст по порядку четырьмя способами. Можно доказать, что число возможных трафаретов, то есть количество ключей шифра "решетка", составляет Т = 4mk. Этот шифр предназначен для сообщений длины n = 4mk. Число всех перестановок в тексте такой длины составит (4mk)!, что во много раз больше числа Т. Однако, уже при размере трафарета 8´8 число возможных решеток превосходит 4 миллиарда
Шифром вертикальной перестановки (ШВП) называется широко распространенная разновидность шифра маршрутной перестановки. В нем используется прямоугольник, в котором сообщение вписывается обычным способом (по строкам слева направо). Выписываются буквы по вертикали, а столбцы при этом берутся в порядке, определяемом ключом. Пусть, например, этот ключ таков: (5,1,4,7,2,6,3), и с его помощью надо зашифровать сообщение:
ВОТПРИМЕРШИФРАВЕРТИКАЛЬНОЙПЕРЕСТАНОВКИ
Впишем сообщение в прямоугольник, столбцы которого пронумерованы в соответствии с ключом:
| В | О | Т | П | Р | И | М |
| Е | Р | Ш | И | Ф | Р | А |
| В | Е | Р | Т | И | К | А |
| Л | Ь | Н | О | Й | П | Е |
| Р | Е | С | Т | А | Н | О |
| В | К | И | - | - | - | - |
Теперь, выбирая столбцы в порядке, заданном ключом и выписывая последовательно буквы каждого из них сверху вниз, получаем такую криптограмму:
ОРЕЬЕРФИЙА-МААЕО-ТШРНСИВЕВЛРВИРКПН-ПИТОТ-
Число ключей ШВП не более m!, где m – число столбцов таблицы. Как правило, m гораздо меньше, чем длина текста n (сообщение укладывается в несколько строк по m букв), а значит, и m! много меньше n!.
В случае, когда ключ ШВП не рекомендуется записывать, его можно извлекать из какого либо запоминающегося слова или предложения. Для этого существует много способов. Наиболее распространенный состоит в том, чтобы приписывать буквам числа в соответствии с обычным алфавитным порядком букв. Например, пусть ключевым словом будет ПЕРЕСТАНОВКА. Присутствующая в нем буква А получает номер 1. Если какая-то буква входит несколько раз, то ее появление нумеруется последовательно слева направо. Поэтому второе вхождение буквы А получает номер 2. Поскольку буквы Б в этом слове нет, то буква В получает номер 3 и так далее. Процесс продолжается до тех пор, пока все буквы не получат номера. Таким образом, мы получаем следующий ключ:
П Е Р Е С Т А Н О В К А
9 4 10 5 11 12 1 7 8 3 6 2
Date: 2015-06-11; view: 1147; Нарушение авторских прав