Доказательства теорем о длинах хорд, касательных и секущих

Теоремы о длинах хорд, касательных и секущих

Фигура	Рисунок	Теорема
Пересекающиеся хорды		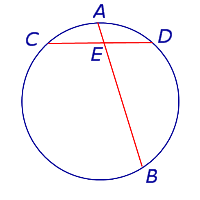Произведения длин отрезков, на которые разбита каждая из хорд, равны: 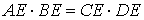Посмотреть доказательство
Касательные, проведённые к окружности из одной точки		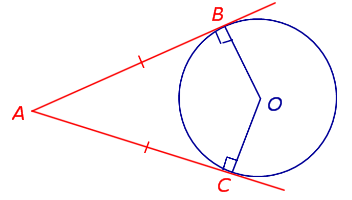Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. AB = AC Посмотреть доказательство
Касательная и секущая, проведённые к окружности из одной точки		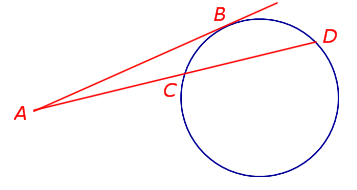Справедливо равенство 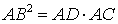Посмотреть доказательство
Секущие, проведённые из одной точки вне круга		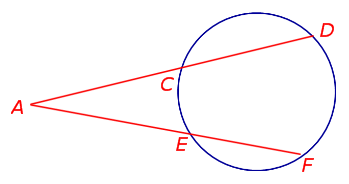Справедливо равенство: 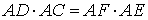Посмотреть доказательство

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1. Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

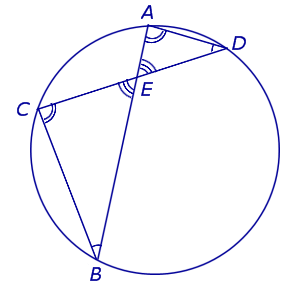
Рис. 1

Тогда справедливо равенство

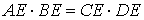
Доказательство. Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

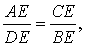
откуда и вытекает требуемое утверждение.

Теорема 2. Предположим, что из точки A, лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

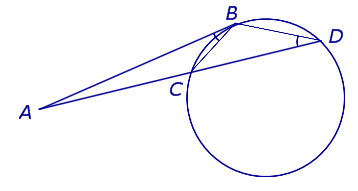
Рис. 2

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

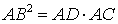
Доказательство. Заметим, что угол ABC образован касательной AB и хордой BC, проходящей через точку касания B. Поэтому величина угла ABC равна половине угловой величины дуги BC. Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC. Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

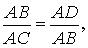
откуда и вытекает требуемое утверждение.

Теорема 3. Предположим, что из точки A, лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Рис. 3

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

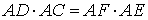
Доказательство. Проведём из точки A касательную AB к окружности (рис. 4).

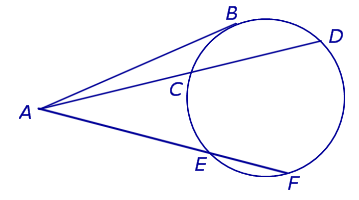
Рис. 4

Точка B – точка касания. В силу теоремы 2 справедливы равенства

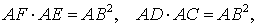
откуда и вытекает требуемое утверждение.