Теорема. 1) Пусть f(x) - бесконечно большая функция при

1) Пусть f (x) - бесконечно большая функция при . Тогда 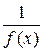- является бесконечно малой функцией при ;

2) Пусть f (x) - бесконечно малая функция при и 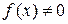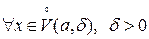. Тогда 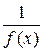- бесконечно большая функция при .

Доказательство.

1) Пусть 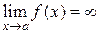. Выберем 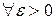и положим .

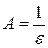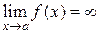Û для выбранного 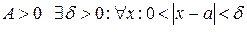выполняется 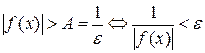(так как 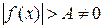, то есть 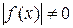в , то 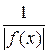имеет смысл) .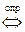

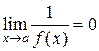2) аналогично.

Теорема. Если при a (х) ~ a ₁(х), b (х) ~ b ₁(х) и существует 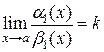, то существует 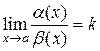, то есть .

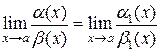Доказательство.

В справедливо: .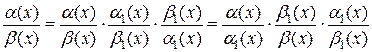

Так как существует 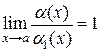, существует 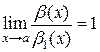и существует 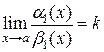, то существует .

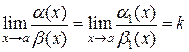Теорема 2. Если функции f (x) и g (x), непрерывны в точке x ₀, то (если ) непрерывны в точке x ₀.

Доказательство.

Доказательство следует из теоремы арифметических операциях над пределами и определения непрерывности. Докажем для .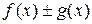

Так как 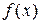и непрерывны в точке x ₀, то по определению 1 и . Тогда по теореме о пределе суммы = .

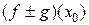Следовательно, функция 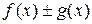непрерывна в точке x ₀.

Теорема (необходимое и достаточное условие дифференцируемости). Для того, чтобы функция f (x) была дифференцируема в точке х ₀ необходимо и достаточно_, чтобы она в этой точке имела производную 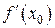, при этом .

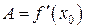Доказательство.

1) Необходимость.

Пусть f (x) дифференцируема в точке х _0, т. 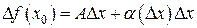е. , где 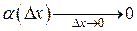. Пусть 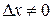. Тогда .

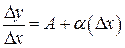Так как существует правой части: , то существует и левой части: 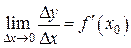, и эти пределы равны: .

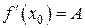2) Достаточность.

Пусть существует 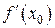, то есть существует 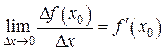. Тогда по необходимому и достаточному условию существования предела функции в точке , где - бесконечно малая при 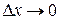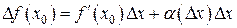. Следовательно, по определению (1) f (x) дифференцируема в точке х _0.

Теорема. Если функции u = u (x) и v = v (x) дифференцируемы в точке х, то в этой точке дифференцируемы их сумма, произведение и (при условии, что 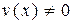) частное, при этом справедливы равенства

, (1)

, (2)

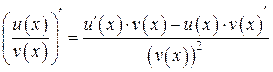. (3)

Доказательство.

1) Пусть 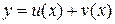. Придадим переменной х приращение 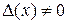. Тогда функции u и v получат приращения D u и D v соответственно. Тогда

,

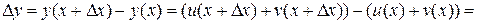
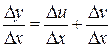. (4)

Пусть 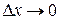, так как u и v дифференцируемы в точке х, то существует и существует . Следовательно, существует правой части равенства (4): 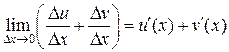. Значит, и существует и левой части .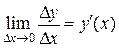

Переходя в (4) к , получим .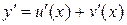

2) Пусть y = u (x) v (x). Придадим точке х приращение 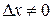. Функции u = u (x) и v = v (x) получат приращения 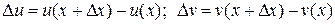. Тогда

,

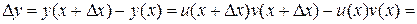
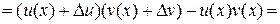
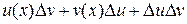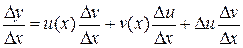. (5)

Пусть 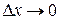. Так как u (x) и v (x) дифференцируемы в точке х, то существует и существует . Так как функция u (x) дифференцируема в точке х, то она непрерывна в этой точке, значит, Поэтому существует

.

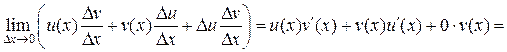
Так как существует правой части равенства (5), то существует и левой части, то есть существует 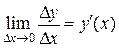. Переходя в (5) к получим

.

Теорема (Свойства неопределённого интеграла)

1. ,

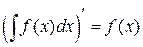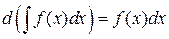
Доказательство.

.

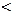
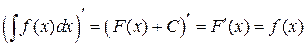
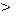
2.

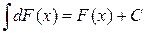
Доказательство.

dF (x)= F' (x) dx = f (x) dx Þ .

3. Если f (x) имеет первообразную на < a; b > и к ≠0, то функция кf (x) тоже имеет первообразную на < a; b >, причём

. (1)

Доказательство.

(kF (x)) ' = kF' (x)= кf (x) Þ функция kF является первообразной для kf на < a; b > =>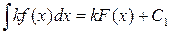

Далее 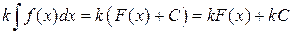. Итак, левая часть равенства (1) представляет собой совокупность функций kF (x)+ C ₁, а правая состоит из функций вида kF (x)+ kC. В силу произвольности С ₁ и С оба множества совпадают.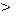

4. Если функции f и g имеют первообразные на < a; b >, то и функция f ± g имеет на < a; b > первообразную, причём

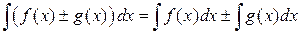. (2)

Доказательство.

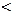Пусть 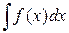= F (x)+ C ₁, = G (x)+ C ₂.

Рассмотрим функцию Ф (x)= F (x)± G (x),

Ф' (x)= F' (x)± G' (x)= f (x)± g (x) Þ 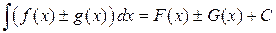. Следовательно, левая часть равенства (2) состоит из функций F (x)± G (x)+ C, а правая из функций (F (x)+ C ₁)±(G (x)+ C ₂)= F (x)± G (x)+ C ₁± C ₂. Ввиду произвольности С ₁, С ₂, С эти множества совпадают.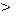

Свойства 3 и 4- линейные свойства интеграла.

Date: 2015-07-02; view: 433; Нарушение авторских прав