
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Доказательство
|
|
Необходимый минимум теорем с доказательствами
Теорема. Любая сходящаяся последовательность 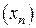 имеет только один предел.
имеет только один предел.
Доказательство.
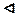 (От противного)Пусть
(От противного)Пусть 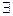 последовательность
последовательность 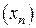 , которая имеет 2 предела:
, которая имеет 2 предела: 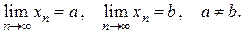 Тогда по определению предела
Тогда по определению предела
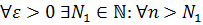
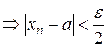 ,
, 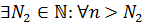
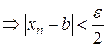 .
.
Обозначим 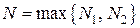 . Тогда
. Тогда  выполнено
выполнено 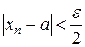 и
и 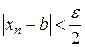 . Тогда
. Тогда 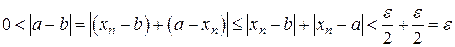 .
.
Получили, что положительное фиксированное число 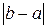 меньше любого положительного числа
меньше любого положительного числа 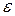 (его можно брать сколь угодно малым), следовательно b-а =0 и значит, а=b.
(его можно брать сколь угодно малым), следовательно b-а =0 и значит, а=b.
Полученное противоречие доказывает теорему. 
Теорема. (Необходимое условие сходимости) Всякая сходящаяся последовательность ограничена.
Доказательство.
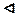 Пусть
Пусть 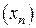 сходящаяся последовательность, то есть
сходящаяся последовательность, то есть 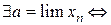
 выполнено
выполнено 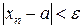 .
.
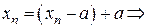
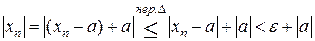 .
.
Значит,  выполнено
выполнено 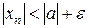 .
.
Обозначим М = 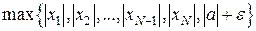 . Тогда " n
. Тогда " n 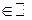 выполнено
выполнено 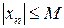 , то есть (по определению) последовательность
, то есть (по определению) последовательность 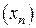 ограничена.
ограничена. 
Теорема. (Необходимое и достаточное условие сходимости последовательности) 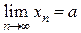
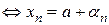 , где
, где 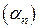 - БМП, то есть
- БМП, то есть 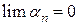 .
.
Доказательство.
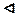 1) Необходимость.
1) Необходимость.
Пусть 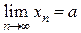 . Рассмотрим последовательность
. Рассмотрим последовательность 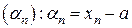 .
.
По определению предела 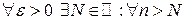 выполнено
выполнено 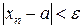 .
.
Следовательно, для последовательности 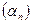 имеем:
имеем: 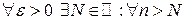 выполнено
выполнено 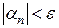 . Значит,
. Значит, 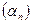 - БМП Þ
- БМП Þ  , где
, где 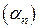 - БМП.
- БМП.
2) Достаточность. 
Пусть  , где
, где 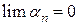 .
.
По определению предела 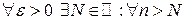 выполнено
выполнено 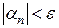 . Так как
. Так как
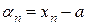 , то
, то 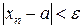 " n>N Þ
" n>N Þ 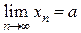 .
. 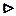
Теорема.  Если
Если 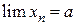 ,
, 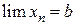 , то
, то
1) 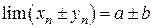 ,
,
2) 
Доказательство.
 По теореме -необходимое и достаточное условие сходимости-
По теореме -необходимое и достаточное условие сходимости-  ,
, 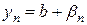 , где
, где 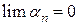 ,
, 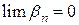 .
.
1) 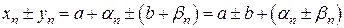 .
.
Так как 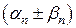 - БМП, то
- БМП, то 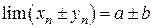 .
.
2) 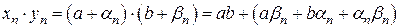
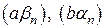 - БМП,
- БМП, 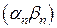 - БМП,
- БМП, 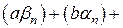
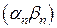 -БМП. Следовательно,
-БМП. Следовательно, 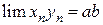 .
. 
Теорема. 1) Любая неубывающая, ограниченная сверху последовательность имеет конечный предел.
2) Любая невозрастающая, ограниченная снизу последовательность имеет конечный предел.
Доказательство.
 1)
1) 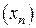 - ограниченная сверху
- ограниченная сверху 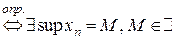 .
.
Докажем, что 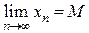 .
.
Выберем  . Тогда по определению 1' для этого e выполняется два условия:
. Тогда по определению 1' для этого e выполняется два условия:
1)  ,
,
2) 
Так как 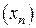 - неубывающая, то
- неубывающая, то  .
.
Следовательно,  выполнены условия 1) и 2), значит,
выполнены условия 1) и 2), значит,  выполнено
выполнено  . Т. е.
. Т. е.  Þ
Þ 
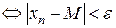 .
.
Итак, 
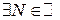 :
:  выполняется
выполняется 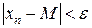
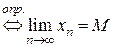 .
.
Заметим, что из условия 1) следует, что  .
.
2) Доказывается аналогично.
Устанавливается, что 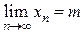 и, следовательно,
и, следовательно, 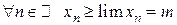 .
. 
Теорема. Для того, чтобы функция f имела предел в точке a необходимо и достаточно, чтобы в этой точке существовали равные между собой односторонние пределы. При этом общее значение односторонних пределов равно пределу функции в точке а:
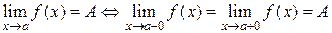
Доказательство.
 1) Необходимость.
1) Необходимость.
 и
и 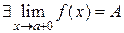 . Это следует из определения предела и определения односторонних пределов.
. Это следует из определения предела и определения односторонних пределов.
2)Достаточность.
Пусть существуют односторонние пределы, равные А. Возьмем 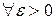 . Тогда согласно определению 2
. Тогда согласно определению 2
 :
: 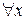 :
: 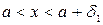 выполняется
выполняется 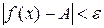 ,
,
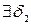 :
: 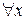 :
:  выполняется
выполняется 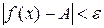 .
.
Выберем 
 :
: 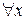 :
:  выполняется
выполняется 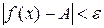 .
.

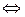
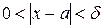
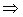 выполняется определение предела
выполняется определение предела 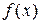 в точке а.
в точке а. 
Теорема. (Единственность предела). Любая функция в точке может иметь только один предел.
Доказательство.
 Пусть
Пусть 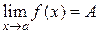 ,
, 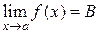 и
и  .
.
Возьмем (xn): xn 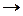 a. Рассмотрим (f (xn)). По определению предела функции по Гейне
a. Рассмотрим (f (xn)). По определению предела функции по Гейне 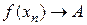 и
и 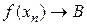 . Но по теореме о единственности предела последовательности отсюда следует, что А=В.
. Но по теореме о единственности предела последовательности отсюда следует, что А=В.
Полученное противоречие доказывает теорему. 
Теорема. Пусть 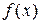 и
и  определены в некоторой проколотой окрестности точки а
определены в некоторой проколотой окрестности точки а  и
и 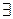
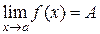 ,
, 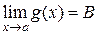 . Тогда в точке а существуют пределы суммы, разности, произведения и частного (при условии, что
. Тогда в точке а существуют пределы суммы, разности, произведения и частного (при условии, что 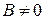 и
и 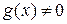 в
в  ), причем
), причем
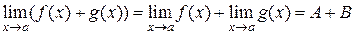 ,
,
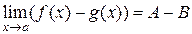 ,
,
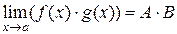 ,
,
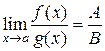 при
при 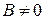 и
и 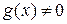 в
в  .
.
Доказательство.
 Докажем для суммы, остальное – аналогично.
Докажем для суммы, остальное – аналогично.
Возьмём 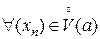 :
: 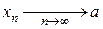 . Так как
. Так как 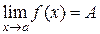 и
и 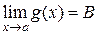 , то по определению предела функции по Гейне
, то по определению предела функции по Гейне 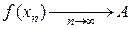 ,
, 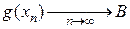 . По теореме о пределе суммы последовательностей последовательность
. По теореме о пределе суммы последовательностей последовательность  также имеет предел, причем
также имеет предел, причем 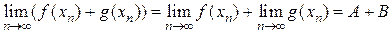 .
.
Получили, что 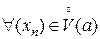 :
: 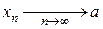 последовательность
последовательность  сходится к числу А+В (
сходится к числу А+В (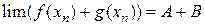 )
) 
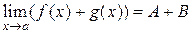 .
. 
Теорема. 1) Сумма, разность и произведение двух бесконечно малых функций в точке а является бесконечно малой функцией в точке а.
2) Произведение бесконечно малой функции в точке а на ограниченную в окрестности точки а функцию является бесконечно малой функцией в точке а.
Доказательство.
 1) Пусть f (x), g (x) - бесконечно малые в точке а функции. Докажем, что f (x)+ g (x) - бесконечно малая функция в точке а. Выберем
1) Пусть f (x), g (x) - бесконечно малые в точке а функции. Докажем, что f (x)+ g (x) - бесконечно малая функция в точке а. Выберем 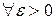 . По определению:
. По определению: 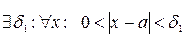 выполняется
выполняется 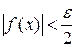 ,
,
 выполняется
выполняется 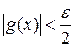 .
.
Возьмём  Þ
Þ  выполняется
выполняется 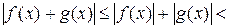
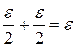
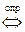
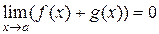 .
.
Разность и произведение – аналогично: 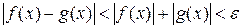 ,
,
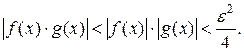 (можно взять не
(можно взять не 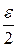 , а
, а 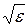 ).
).
2) Пусть f (x) – ограничена в окрестности точки а, а g (x) - бесконечно малая функция в точке а.
Тогда по определению существует 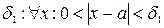 выполняется
выполняется 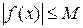 ;
;
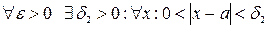 выполняется
выполняется  .
.
Возьмём  Þ
Þ  выполняется
выполняется 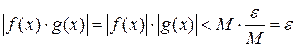 Û
Û 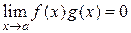 .
. 
Date: 2015-07-02; view: 497; Нарушение авторских прав