Энтропия информации

Э нтропия – содержательность, мера неопределенности информации.

Э нтропия – математическое ожидание H(x) случайной величины I(x) определенной на ансамбле {Х, р(х)}, т.е. она характеризует среднее значение количества информации, приходящееся на один символ.

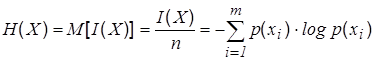. (6)

Определим максимальное значение энтропии H_max(x). Воспользуемся методом неопределенного множителя Лагранжа -l для отыскания условного экстремума функции [6]. Находим вспомогательную функцию:

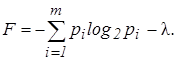(7)

Представим вспомогательную функцию F в виде:

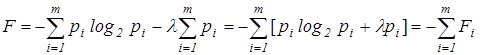. (8)

Найдем максимум этой функции

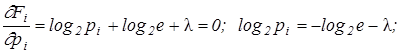т. к.

.

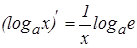Как видно из выражения, величина вероятности p_i не зависит от i, а это может быть в случае, если все p_i равны, т.е. p₁ =p₂ =…=p_m =1/m.

При этом выражение для энтропии равновероятных, независимых элементов равно:

. (9)

Найдем энтропию системы двух альтернативных событий с вероятностями p₁ и p₂. Энтропия равна:

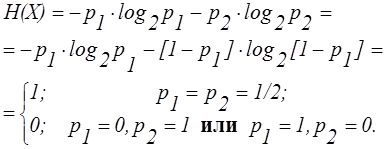
Энтропия источника при наличии Корреляционных свя­зей между буквами.

В реальных источниках буквы появляются с различной вероятностью, причем эта вероятность зависит от того какие буквы предшествовали рассмат­риваемой. Т.е. такие источники формируют последовательность, которая под­чиняется закономерностям цепи Моркова. Напомним, что цепью Моркова порядка 1 называется такая последовательность зависимых испытаний, при которой вероятность появления какой-то реализации при этом испытании зависит от результатов 1 предыдущих испытаний и не зависит от результатов (1+1) и более ранних опытов.

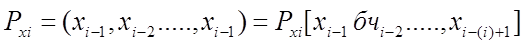
Таким образом, с точки зрения прогнозирования вероятности появле­ния очередной буквы, нас интересуют предыдущие 1 букв (предыстория на 1 шагов назад).

Если источник имеет алфавит длиной п, то можно составить 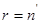различных слов, каждое из которых будет определять с какой вероятностью появится та или иная последующая буква. Обозначим текущее конкретное состояние источника буквой q, а вероятность перехода источника в это со­стояние 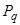,. Тогда учитывая, что максимальное число таких состояний r можно записать, что . Если считать, что источник уже перешел в q-ое состояние, то можно задать условными вероятностями появление отдельных букв алфавита на его выходе . Очевидно, что .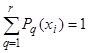

Тогда условная энтропия источника (при условии, что он находится в фиксирован­ном q-ом состоянии):

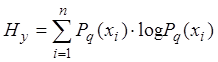
Для перехода к безусловной энтропии необходимо усреднить услов­ную энтропию с учетом вероятностей перехода источника в различные со­стояния.

Задание:

1. Определить энтропию бинарного симметричного источника, т.е. при отсут­ствии корреляционных связей.

2. Определить энтропию источника, если в нем имеются корреляционные связи только между соседними буквами и вероятности появления одинаковых букв равны 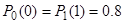, а разных букв .

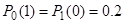3. Определить количество информации и энтропию сообщения из пяти букв, если число букв в алфавите равно 32 и все сообщения равновероятные.

Date: 2015-07-02; view: 324; Нарушение авторских прав