Краткие теоретические сведения. для системы, состоящей из т элементов, каждый из которых может находиться в одном из п состояний

Ход работы

По формуле Хартли:

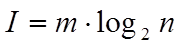
для системы, состоящей из т элементов, каждый из которых может находиться в одном из п состояний.

Т.е. m-длина слова

n-длина алфавита

Рассчитаем количество информации, подставив заданные значения в формулу Хартли.

Количество информации равно:

I = n log m = 8 log₂ 2 = 8 бит.

Вывод

1. Количество информации в сообщении обратно – пропорционально вероятности появления данного сообщения.

2. Свойство аддитивности – суммарное количество информации двух источников равно сумме информации источников.

3. Для события с одним исходом количество информации равно нулю.

4. Количество информации в дискретном сообщении растет в зависимости от увеличения объема алфавита – m.

Министерство образования и науки, молодёжи и спорта Украины

Одесский национальный политехнический университет

Институт компьютерных систем

Кафедра компьютеризированных систем управления

Лабораторная работа №2

По дисциплине: «Теория информации»

На тему: «Определение количества информации по Шеннону»

Выполнила:

студентка группы АТ-092

Задыр И.Г.

Проверила:

доц. Трофименко Т.Г.

Одесса 2012г.

Краткие теоретические сведения

Энтропия источника сообщения (формула Шенона)

К. Шенон в 1948 году ввел вероятностную меру информации, и создал достаточно аналитический аппарат, на который операется вся современная теория информации.

Источник сообщений выбирает и посылает приемнику буквы по оп­ределенному вероятностному закону. До прихода очередной буквы в прием­ник была неопределенность, какую букву выберет и пошлет в канал связи ис­точник. После приема очередной буквы у приемника снимается эта неопреде­ленность. Таким образом, передача сообщений это процедура снятия неопре­деленности у приемника.

Например, бинарный источник посылает букву 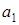с вероятностью

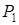и букву 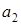с вероятностью 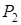. Если 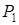= 0,9 и 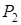= 0,1, то появления у приемника а, будет менее неожиданным, чем 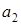и эта буква будет нести меньше информации. При возрастании вероятности появления 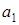в пределе значение 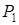стремится к единице. При 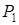= 1 процесс становится полно­стью детерминированным, заранее полностью предсказанным, а количество информации в этой букве становится равным нулю. По мере уменьшения ве­роятности 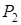появление буквы 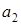будет все более редким, все более неожиданным, а количество информации в этой букве возрастает и при 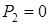стремится к бесконечности (но эта буква никогда не будет появляться). Э предложенное К. Шенноном рассуждение позволило ему ввести понятие| среднем количестве информации, приходящемся на одну букву, которое должно учитывать вероятность ее появления.

Очень длинное слово длиной т (для которого количество i-тых букв 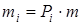разобьем на группы букв таким образом, чтобы в каждую групп

входили буквы с одинаковой вероятностью появления. Тогда к каждой групп может быть применима формула Хартли. Если буквы равновероятны, топри

алфавите п вероятности появления каждой буквы , формулу Хартли

можно записать в виде . Тогда после разбиения алфавита на группы равновероятных букв, получим:

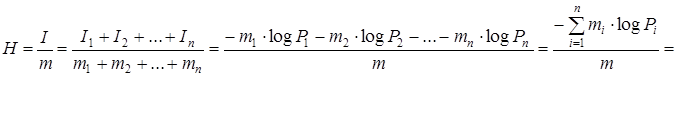
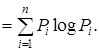
Задание:

1. Определить количество информации в сообщении из 8 двоичных символов (n = 8, m = 2), если вероятности равны:

p_i0 = 3/4; p_i1 = 1/4.

2. Определить энтропию источника, относительная приведенная погрешность сигнала которого 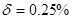. Причем 40 букв из 200 букв алфавита имеет вероятность появления 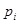=0.9, а остальные 160 букв – вероятность появления 0.1.

Date: 2015-07-02; view: 369; Нарушение авторских прав