Поглощение энергии. Закон Бугера-Ламберта

Электромагнитная волна при прохождении через среду ослабляется вследствие поглощения и рассеяния.

Поглощение света - это явление уменьшения энергии световой волны при ее распространении в веществе, происходящее вследствие преобразования энергии волны во внутреннюю энергию вещества. Поглощение света может вызывать нагревание вещества, возбуждение и ионизацию атомов или молекул, фотохимические реакции и другие процессы в веществе.

Рассеяние света - явление преобразования света веществом, сопровождающееся изменением направления распространения света и проявляющееся как несобственное свечение вещества, обусловленное вынужденными колебаниями электронов в атомах рассеивающей среды под действием падающего света. Оно происходит в оптически неоднородной среде, показатель преломления которой изменяется скачками от точки к точке среды вследствие флуктуаций плотности среды (молекулярное рассеяние), либо за счет присутствия в среде инородных малых частиц (мутная среда - дым, туман, эмульсии и др.). Рассеяние света в мутных средах на частицах, размеры которых малы по сравнению с длиной волны, называется явлением Тиндаля. Теория молекулярного рассеяния разреженными газами была развита польским физиком М. Смолуховским, а жидкостями - А. Эйнштейном.

Закон ослабления света был экспериментально установлен французским ученым П. Бугером и впоследствии теоретически выведен немецким ученым И.Ламбертом. Пусть пучок параллельных лучей, начальная интенсивность которых при х =0 равна I₀ распространяются в поглощающей среде (рис. 1.2).

Пройдя в среде путь х, свет за счет поглощения и рассеяния ослабляется и его интенсивность I становится меньше первоначальной I₀. Выделим участок среды толщиной dх. Интенсивность света, прошедшего путь х + dх, равная I - dI, будет меньше, чем I, то есть dI < 0 (ослабление). Величина - dI представляет собой лучистый поток, поглощенный и рассеянный на участке dх и она, очевидно, пропорциональна толщине этого участка dх и интенсивности падающего (на этот участок) света I, т.е.

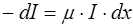. (1.35)

Коэффициент пропорциональности m называется коэффициентом ослабления света.

Разделим переменные в выражении (1.35):

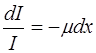. (1.36)

Проинтегрируем выражение (1.36) по интенсивности от I₀ до I, а по пройденному в среде пути от 0 до x:

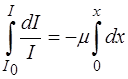. (1.37)

Получим:

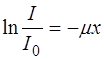. (1.38)

Потенцируем результат (1.38):

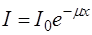. (1.39)

Полученное выражение носит название закона Бугера-Ламберта. На рис. 1.3 показан график (экспонента) этой зависимости.

Коэффициент ослабления m складывается из коэффициента поглощения и коэффициента рассеяния:

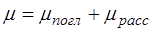. (1.40)

Первый из них (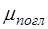) характеризует долю поглощенной энергии (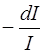) на единице пути (dх = 1), перешедшей в другие формы энергии в основном в тепловую. Второй (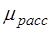) аналогичным образом характеризует долю энергии первичного пучка, унесенную рассеянным светом во все стороны.

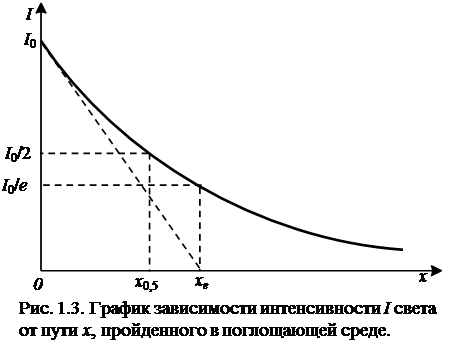Коэффициент ослабления m зависит только от длины волны света, химической природы и состояния вещества и не зависит от интенсивности света. С.И. Вавилов установил, что закон Бугера-Ламберта выполняется в довольно широких пределах изменения интенсивности света. Зависимость коэффициента m от длины волны, характеризующая спектр поглощения света в этой среде, связана с явлением резонанса при вынужденных колебаниях электронов в атомах и атомов в молекулах диэлектрика. Он имеет размерность обратной длины (м^-1) и называется линейным коэффициентом ослабления светового потока. Его физический смысл легко установить, преобразовав уравнение (1.35) следующим образом:

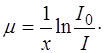(1.41)

Если толщина слоя 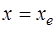, отношение 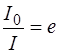. Тогда из (1.41) имеем:

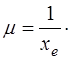(1.42)

Таким образом, коэффициент ослабления численно равен величине, обратной толщине слоя вещества, по прохождении которого интенсивность света уменьшается в е раз (е = 2,7182.. – основание натуральных логарифмов). На рис. 1.5 показано также, что 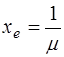характеризует расстояние, на котором свет поглотился бы полностью, если бы абсолютное поглощение (-dI) не убывало по мере снижения интенсивности проходящего потока.

На рис. 1.3 (в логарифмических координатах) отмечена еще так называемая толщина слоя половинного ослабления х _0,5, определяемая из условия:

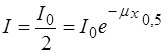, (1.43)

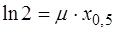, (1.44)

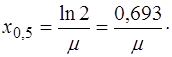(1.45)

Часто пользуются массовым коэффициентом ослабления m_r лучей, так как коэффициент ослабления обычно пропорционален плотности r.

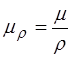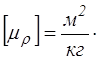, (1.46)

В этом случае закон Бугера-Ламберта принимает вид:

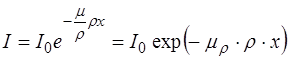. (1.47)

Произведение r×х при этом характеризует массу поглощающего вещества, приходящуюся на единицу площади прошедшего пучка .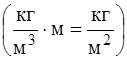

При поглощении света веществами, растворенными в практически не поглощающем растворителе (например, в чистой воде), коэффициент ослабления часто пропорционален концентрации растворенного вещества С:

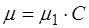. (1.48)

Эта зависимость была получена на опыте немецким ученым А. Бером и называется правилом Бера.

Для таких растворов закон поглощения (закон Бугера-Ламберта-Бера) принимает вид:

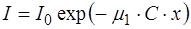, (1.49)

где 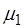- новый коэффициент ослабления (поглощения), не зависящий от концентрации и характерный для молекулы поглощающего вещества. Следует отметить, что в реальных газах и растворах закон Бугера-Ламберта-Бера выполняется далеко не всегда.

Измеряя поглощение света слоем такого раствора (толщиной х) и зная коэффициент ослабления 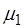, можно отсюда найти концентрацию исследуемого раствора:

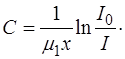(1.50)

При достаточно больших значениях интенсивности света закон Бугера-Ламберта нарушается: показатель поглощения диэлектрической среды начинает зависеть от интенсивности света, уменьшаясь с ее ростом, что противоречит классической физике. Ответ дает квантовая теория: при поглощении света часть молекул среды переходит в возбужденное состояние. Такие молекулы не могут участвовать в дальнейшем поглощении света до тех пор, пока они не вернутся, растратив всю свою энергию, в невозбужденное (стационарное) состояние. Закон Бугера-Ламберта выполняется лишь в том случае, если доля возбужденных молекул незначительна.

Можно осуществить такое неравновесное состояние среды, при котором доля возбужденных молекул будет столь велика, что показатель поглощения m * становится отрицательным. Это явление, соответствующее отрицательности m *, используется в квантовых генераторах радиоволн и света (лазерах).Тогда такая среда называется активной и происходит усиление света по закону Бугера-Ламберта-Фабриканта:

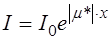. (1.51)

Кроме того, в случае, когда коэффициент поглощения m не является постоянным, а зависит от координаты x (m = m (x)), то при интегрировании (1.37) и потенцировании результата получим более общий вид закона поглощения:

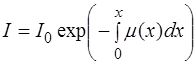. (1.52)

Закон Бугера-Ламберта в принципе применим для всего диапазона электромагнитных излучений видимого света, инфракрасных и ультрафиолетовых лучей, радиоволн, рентгеновских и гамма-лучей. Однако при его практическом применении следует учесть, что при некоторых условиях он может иметь лишь приближенный характер. Коэффициент ослабления зависит от длины волны света и закон Бугера-Ламберта справедлив для монохроматического света, если частота света далека от резонанса с частотами колебаний электрических зарядов в атомах вещества.

1.5 Электромагнитная волна на границе раздела сред

Выясним, как ведет себя электромагнитная волна при падении на границу раздела двух однородных изотропных прозрачных диэлектриков. Пусть магнитная проницаемость обоих диэлектриков 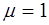. Для установления основных закономерностей достаточно ограничиться рассмотрением случая, когда плоская волна нормально падает на плоскую границу раздела диэлектриков с показателями преломления 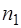и 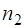. Волна идет из среды с показателем преломления 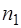в среду с показателем преломления .

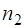Обозначим электрическую составляющую в падающей, отраженной и преломленной волне соответственно как 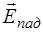, , 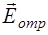, 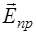а магнитную составляющую как , , .

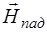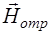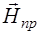Ясно, что колебания векторов 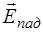, 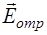и 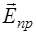проис-ходят в одной плоскости. Это же относится и к векторам 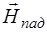, 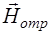и 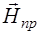. Направления распространения волн обозначим волновыми векторами 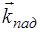, , 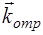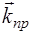. На рис. 1.4 показано поведение векторов 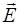, 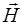и 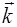падающей, отраженной и преломленной волны в непосредственной близости от границы раздела.

Воспользуемся граничными условиями для тангенциальных составляющих векторов 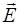и 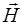. Как известно из курса электромагнетизма, тангенциальная составляющая векторов 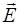и 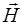не изменяется при переходе границы раздела диэлектриков:

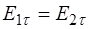, (1.53)

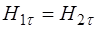. (1.54)

Поскольку вектора 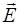и 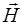располагаются в плоскости границы раздела и перпендикулярны направлению распространения, то (1.53) и (1.54) можно записать для нашего случая как:

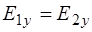, (1.55)

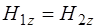. (1.56)

Тангенциальная составляющая вектора 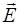(проекция на ось Y) в первом диэлектрике складывается из проекций на ось Y векторов 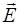падающей и отраженной волны:

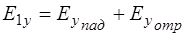, (1.57)

а во втором диэлектрике равна проекции вектора 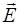прошедшей волны:

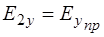. (1.58)

Поскольку поглощения энергии при переходе границы раздела нет, тангенциальная составляющая не изменяется, что позволяет нам, приравняв (1.57) и (1.58), записать:

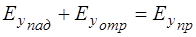. (1.59)

Основываясь на (1.56) запишем аналогичное выражение для вектора :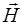

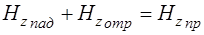. (1.60)

Согласно соотношению между амплитудами векторов 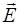и 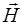(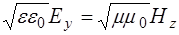), а также приняв равными магнитные проницаемости диэлектриков (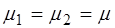) получаем следующие уравнения для проекций вектора 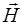во всех трёх волнах:

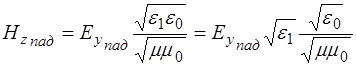, (1.61)

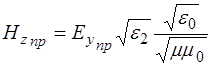, (1.62)

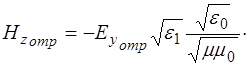(1.63)

В уравнении (1.63) учтено то, что в отраженной волне вектора 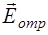, 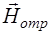и 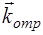должны составлять правую тройку. Отсюда и знак минус в уравнении (1.63).

Учитывая уравнения (1.61) – (1.63), выражение (1.60) можно записать так:

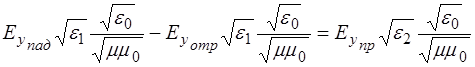, (1.64)

или

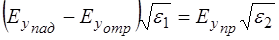. (1.65)

Из (1.65) видно, что:

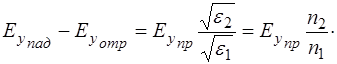(1.66)

Итак, мы получили систему из двух уравнений:

,

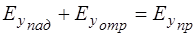(1.67)

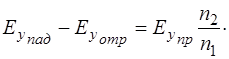
Решая систему (1.67), получим выражения для прошедшей и отраженной волны:

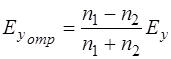, (1.68)

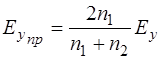, (1.69)

или то же в векторном виде:

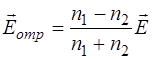, (1.70)

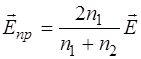. (1.71)

Таким образом, мы получили выражения для коэффициентов отражения и прохождения электромагнитной волны:

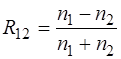, (1.72)

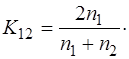(1.73)

Из полученных выражений (1.72) и (1.73) следует, что:

1. Вектор 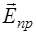всегда сонаправлен с вектором 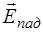, т.е. оба вектора колеблются синфазно – при прохождении границы раздела сред фаза электромагнитной волны не претерпевает скачка.

2. Если электромагнитная волна отражается от среды с меньшим показателем преломления (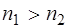), то ее фаза не меняется. Если же волна отражается от оптически более плотной среды (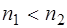), то дробь оказывается отрицательной, а это говорит о том, что направление вектора 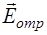противоположно направлению вектора 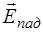, то есть колебания вектора 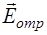происходят в противофазе с колебаниями вектора 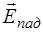, т.е. при отражении волны от оптически более плотной среды ее фаза скачком изменяется на p. Поскольку с потерей разности фаз в 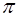связана потеря полволны в теории волн, и в особенности в оптике, говорят, что при отражении от более плотной среды луч теряет полволны.

1.6 Принцип Гюйгенса

В 1690 году Гюйгенс предложил способ построения фронта волны в момент t + D t по известному положению фронта волны в момент времени t. Согласно принципу Гюйгенса, каждая точка поверхности, которую в данный момент достигла волна, является центром вторичных волн. Огибающая этих волн дает фронт волны в следующий момент.

Световой луч – это нормаль к волновой поверхности. Такое определение справедливо, если диаметр волнового фронта D значительно больше длины световой волны l:

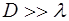. (1.74)

Условие (1.74) выполняется в случае расходящихся пучков лучей. Если пучки лучей сходящиеся, то их фронт должен превратиться в точку, что невозможно, т. к. изображение точки получится в виде дифракционного пятна и понятие о луче теряет смысл.

Вторым условием применимости понятия лучей является:

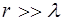, (1.75)

т.е. радиус кривизны волны должен быть значительно больше длины волны.

Date: 2015-06-11; view: 7521; Нарушение авторских прав