Распространение света

Электромагнитная природа света

Распространение света

Свет – это электромагнитные волны, длины которых лежат в оптическом диапазоне. Этот диапазон подразделяют на:

– инфракрасное излучение: l = 1 мм ¸ 0,76 мкм;

– видимый свет: l = 0,76 ¸ 0,40 мкм;

– ультрафиолетовое излучение: l = 0,40 ¸ 0,01 мкм.

Соответствующие длины волн указаны в вакууме.

Человеческий глаз имеет различную чувствительность к свету с различными длинами волн. Наиболее чувствителен глаз к волнам с длиной 555 нм (зеленая часть спектра).

Свет представляет собой сложное явление: в одних случаях он ведет себя как электромагнитная волна, в других – как поток частиц (фотонов). Так, в одних явлениях (интерференция, дифракция, поляризация, оптическая анизотропия кристаллов, преломление света на границе двух сред) чётко проявляются волновые свойства света. В других явлениях (фотоэффект, излучение абсолютно чёрного тела, спектры атомов и молекул) свет ведёт себя как поток фотонов. Третью группу явлений (давление света, отражение света, дисперсия) можно объяснить и с волновой, и с корпускулярной точки зрения. Такое свойство света называется корпускулярно-волновым дуализмом. Дуализм присущ всем электромагнитным колебаниям, с уменьшением частоты колебаний усиливаются волновые свойства, с увеличением частоты превалируют корпускулярные свойства.

Поскольку электромагнитная волна распространяется с различной скоростью в различных средах, то есть смысл выделить в отдельную величину отношение скорости с распространения в вакууме к скорости u распространения в веществе:

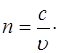(1.1)

Эта величина называется абсолютным показателем преломления этой среды и зависит от электрической и магнитной проницаемости среды. Поскольку скорость света в среде с проницаемостями e и m равна:

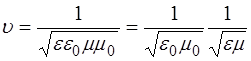, (1.2)

а скорость света в вакууме:

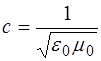, (1.3)

то абсолютный показатель преломления

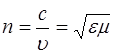. (1.4)

Для подавляющего большинства прозрачных веществ магнитная проницаемость очень близка к единице, и поэтому можно считать, что показатель преломления пропорционален корню квадратному из диэлектрической проницаемости среды:

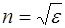. (1.5)

Показатель преломления характеризует оптическую плотность среды. Среда с бόльшим показателем преломления n называется оптически более плотной, чем среда с меньшим n.

В средах с различной оптической плотность изменяется не только скорость распространения электромагнитной волны, но и длина волны. В случае распространения в вакууме колебаний с частотой n длина волны равна:

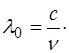(1.6)

В среде же, в которой фазовая скорость волны равна:

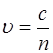, (1.7)

длина волны имеет значение:

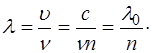(1.8)

В электромагнитной волне колеблются векторы 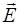и 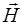. Однако воздействие на вещество оказывает электрический вектор 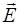. Поэтому в тех случаях, когда говорят о световом векторе, имеют в виду вектор напряженности электрического поля.

1.2 Энергия электромагнитной волны

Электромагнитная волна, как и всякая другая бегущая волна, переносит энергию. Энергия поля может быть найдена как интеграл от плотности энергии по тому объёму, в котором эта энергия распределена.

Плотность энергии электромагнитной волны в обычной изотропной среде с проницаемостям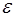и и 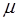равна сумме плотностей энергии электрического и магнитного полей:

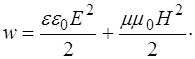(1.9)

Поскольку магнитная и электрическая составляющая в волне изменяются синфазно, то они одновременно достигают максимального значения, и в данной среде справедливо соотношение:

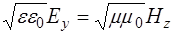, (1.10)

или, возведя в квадрат:

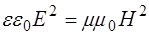, (1.11)

откуда

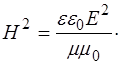(1.12)

Подставим (1.12) в (1.9):

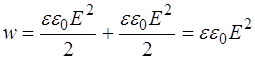. (1.13)

Из (1.13) видно, что плотность энергии в бегущей волне равна удвоенной плотности магнитной энергии. Запишем уравнение (1.13) с учетом (1.10):

, (1.14)

где 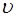– скорость волны.

Умножив плотность энергии 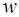на скорость волны 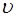, получим плотность потока энергии электромагнитной волны:

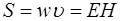. (1.15)

Векторы 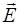и 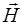взаимно ортогональны и образуют с направлением распространения волны правовинтовую систему. Поэтому векторное произведение 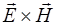совпадает по направлению с направлением переноса энергии, и модуль векторного произведения равен 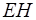. Исходя из этого плотность потока электромагнитной энергии можно представить в виде вектора 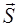плотности потока:

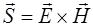. (1.16)

Вектор 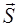называется вектором Пойнтинга. Он характеризует энергию, переносимую электромагнитной волной в единицу времени через единичную площадку.

Рассмотрим бегущую гармоническую электромагнитную волну, распространяющуюся в положительном направлении оси X. Колебания электрической и магнитной составляющих будут описываться следующими уравнениями:

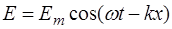, (1.17)

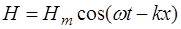, (1.18)

где E_m и H_m – амплитудные значения напряжённости электрического и магнитного поля соответственно.

Плотность энергии такой волны равна:

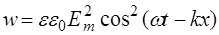, (1.19)

а плотность потока энергии:

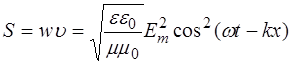. (1.20)

Интенсивность такой волны равна среднему значению плотности потока энергии. Поскольку среднее значение квадрата косинуса равно 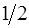, то интенсивность волны оказывается пропорциональна квадрату амплитуды :

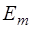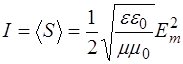. (1.21)

Для большинства оптических сред, т.е. сред, прозрачных для электромагнитного излучения оптического диапазона можно считать, что магнитная постоянная 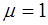. Тогда показатель преломления такой среды пропорционален диэлектрической проницаемости среды:

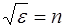. (1.22)

Таким образом, интенсивность волны может быть представлена как:

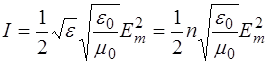. (1.23)

Таким образом, интенсивность электромагнитной волны пропорциональна амплитуде A колебаний вектора 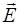напряженности электрического поля, который принято называть световым вектором:

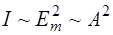. (1.24)

1.3 Импульс электромагнитной волны

Электромагнитная волна, как и всякая другая бегущая волна, переносит энергию. Поглощаясь в каком-либо теле, электромагнитная волна сообщает ему импульс, т.е. оказывает на него некоторое давление. Рассмотрим подробно механизм возникновения давления.

Пусть плоская волна падает по нормали на плоскую поверхность слабо проводящего тела, диэлектрическая и магнитная проницаемости которого 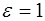и 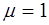(рис. 1.1). На поверхности тела электрическое поле 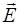волны приведет в движение свободные носители заряда и возбудит в теле ток плотности, сонаправленный с вектором :

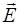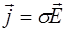, (1.25)

где 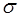– электропроводность тела.

На каждый из носителей тока будет действовать магнитное поле 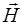волны будет действовать с силой

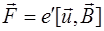, (1.26)

где 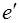– заряд носителя тока;

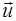– скорость носителя тока.

Тогда сила, действующая на все 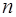носителей, находящихся в единице объема:

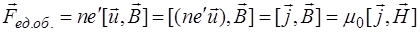, (1.27)

где 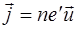– плотность тока.

Направление силы, действующей на тело со стороны электромагнитной волны, совпадает с направлением распространения волны.

Сила, действующая на поверхностный слой, площадь которого равна единице и толщина которого , сообщает в единицу времени импульс:

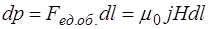, (1.28)

причем векторы 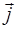и 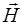взаимно перпендикулярны. В этом же слое за единицу времени поглощается энергия:

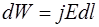, (1.29)

которая выделяется в виде теплоты. И импульс и энергия сообщаются слою той частью волны, которая поглощается этим слоем. Можем взять их отношение, опустив знак дифференциала (так как рассматривается один и тот же малый промежуток времени):

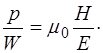(1.30)

Приняв во внимание 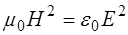, получим отношение:

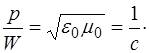(1.31)

Таким образом, электромагнитная волна, несущая энергию 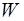, обладает импульсом:

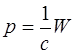. (1.32)

Такое же соотношение имеется между импульсом и энергией для частиц, обладающих нулевой массой покоя. Плотность импульса, то есть импульс, отнесенный к единице объема электромагнитного поля, равен:

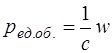, (1.33)

и, поскольку плотность энергии 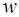связана с модулем вектора Пойнтинга как 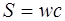, то, учтя сонаправленность векторов 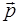и 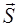, можем записать:

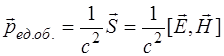. (1.34)

Импульс, сообщаемый единице площади поверхности в единицу времени, равен давлению на эту поверхность. В случае поглощающей поверхности давление на единицу площади будет равно плотности энергии. В случае идеально отражающей поверхности давление будет в два раза больше.

Date: 2015-06-11; view: 843; Нарушение авторских прав