
- Р Р‡.МессенРТвЂВВВВВВВВВжер
- ВКонтакте
- РћРТвЂВВВВВВВВВнокласснРСвЂВВВВВВВВВРєРСвЂВВВВВВВВВ
- Telegram
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВВВВВВРЎР‚
- LiveJournal
- РЎРєРѕРїРСвЂВВВВВВВВВровать ссылку
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Способ 2
|
|
Задача1 Четыре источника
 Из-под земли бьют четыре источника.
Из-под земли бьют четыре источника.
Первый заполняет бассейн за один день, второй – за два дня, третий – за три дня, четвертый – за 4 дня.
За какое время наполнят бассейн все четыре источника?
Способ 1
Скорость заполнения бассейна первым источником – 1 бассейн в день, вторым – 1/2 бассейна в день, третьим – 1/3 и четвертым – 1/4.
Сообща источники заполнят за день
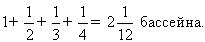
Один бассейн источники, работая сообща, заполнят за

31 минуту и 12 секунд.
Способ 2.
Наименьшее время, которое потребуется каждому из источников, чтобы заполнить целое число бассейнов, – 12 дней,
наименьшее общее кратное продолжительностей заполнения бассейна каждым из источников.
За 12 дней первый источник заполнит 12 бассейнов, второй – 6, третий – 4, четвертый – 3.
Работая вместе 12 дней, источники наполнят 12 + 6 + 4 + 3 = 25 бассейнов.
На заполнение одного бассейна уйдет 12/25 дня.

| Задача 2. Денежный вопрос |
 У мальчика было 75 рублей пяти- и десятирублевыми купюрами.
Если бы пятирублевых купюр было столько, сколько десятирублевых,
а десятирублевых – столько, сколько пятирублевых,
то всего у него оказалось бы 90 рублей.
Сколько было у мальчика в отдельности пяти- и десятирублевых купюр? У мальчика было 75 рублей пяти- и десятирублевыми купюрами.
Если бы пятирублевых купюр было столько, сколько десятирублевых,
а десятирублевых – столько, сколько пятирублевых,
то всего у него оказалось бы 90 рублей.
Сколько было у мальчика в отдельности пяти- и десятирублевых купюр?
|
Решение.
Способ 1. Общая сумма денег по двум вариантам составляет 75 + 90 = 165 р.
В этой сумме купюр двух достоинств поровну (по условию).
Следовательно, количество купюр каждого достоинства здесь равно 65: (10 + 5), а общее число купюр – 22.
Количество купюр, имеющихся у мальчика, вдвое меньше и равно 11.
Если предположить, что все 11 купюр – пятирублевые, у мальчика оказалось бы 55 р., на 20 р. меньше, чем в действительности.
При замене одной пятирублевой купюры на десятирублевую наличная сумма увеличивается на 5 р.
Заменив 4 пятирублевые купюры на десятирублевые (20: 5 = 4), приведем сумму денег у мальчика в соответствие с реальной: 5(11-4) + 10 · 4 = 75 р.
Способ 2. В результате замены пятирублевых купюр десятирублевыми и наоборот сумма денег увеличилась на 15 р.
Отсюда следует, что пятирублевых купюр у мальчика было больше, чем десятирублевых.
Отложим в сторону все имеющиеся десятирублевые купюры и равное им число пятирублевых купюр.
При оговоренной в условии замене эти количества не претерпят изменений. Увеличение суммы на 15 р. обусловлено заменой оставшихся пятирублевых купюр десятирублевыми.
Число этих купюр равно 15: 5 = 3.
Общая стоимость отложенных купюр равна 75 - 15 = 60 р.
Эту стоимость образуют равные количества купюр двух достоинств.
Число пар купюр двух достоинств равно 60: (10 + 5) = 4.
Следовательно, число десятирублевых купюр у мальчика – 4, пятирублевых – на 3 больше, т.е. 7.
| Задача 3. Сколько у Маши монет каждого типа? |
 У Маши в копилке сорок монет, некоторые однокопеечные,
остальные пятикопеечные, на общую сумму один рубль.
Сколько у нее монеток каждого типа? У Маши в копилке сорок монет, некоторые однокопеечные,
остальные пятикопеечные, на общую сумму один рубль.
Сколько у нее монеток каждого типа?
|
Способ 1.
Предположим, что все монеты у Маши - однокопеечные.
Тогда в копилке - 40 копеек, что на 60 копеек меньше, чем нужно.
Теперь заметим, что каждый раз, когда мы заменяем одну однокопеечную монету на пятикопеечную, содержимое копилки увеличивается на 4 копейки.
Значит, чтобы увеличить его на 60 копеек, надо такую замену произвести 60: 4 = 15 раз.
Следовательно, в копилке 15 пятикопеечных монет и (40 - 15) = 25 однокопеечных.
Способ 2
Обозначим: x - количество пятикопеечных монет.
Тогда можно написать: 40 - х + 5х = 100 копеек.
Монет пятикопеечных: х = (100 - 40): 4 = 15 штук.
Монет однокопеечных: 40 - 15 = 25 штук.


| Задача 1. Вышел из срока |
 Чтобы сдать в срок книгу в библиотеку ученик должен был читать ежедневно по 40 страниц.
Однако он читал каждый день на 15 страниц меньше и вернул книгу на 6 дней позже срока.
За сколько дней ученик должен был прочитать книгу? Чтобы сдать в срок книгу в библиотеку ученик должен был читать ежедневно по 40 страниц.
Однако он читал каждый день на 15 страниц меньше и вернул книгу на 6 дней позже срока.
За сколько дней ученик должен был прочитать книгу?
|
| Способ 1. Для прочтения книги в сниженном темпе потребовалось дополнительно 6 дней сверх установленного срока. За эти 6 дней ученик прочитал 25 · 6 = 150 страниц, накопившихся в результате того, что в течение запланированного времени "задолженность" возрастала ежедневно на 15 страниц. В соответствии с первоначальным планом срок прочтения книги составлял 150: 15 = 10 дней. Способ 2. Обозначим: x - намеченный срок прочтения книги. 40x = 25(х + 6); х = 10 (дней). |

Задача 3. Товарный поезд
Товарный поезд шел от А до В со скоростью 60 км/ч,
а возвращался порожняком из В в А со скоростью 80 км/ч.
Весь путь занял 14 ч (не считая времени разгрузки).
Найти расстояние от А до В.
Разделив общую продолжительность поездки (14 часов) в указанном отношении, найдем время движения поезда от А к В:
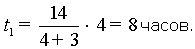 При скорости 60 км/ч поезд прошел за это время путь от А до В 60 ·80 = 480 км.
Способ 2.
Примем расстояние от А до В за единицу. При скорости 60 км/ч поезд преодолел это расстояние за время
При скорости 60 км/ч поезд прошел за это время путь от А до В 60 ·80 = 480 км.
Способ 2.
Примем расстояние от А до В за единицу. При скорости 60 км/ч поезд преодолел это расстояние за время 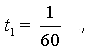 при скорости 80 км/ч – за время при скорости 80 км/ч – за время 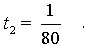 Общая продолжительность движения составляет
Общая продолжительность движения составляет
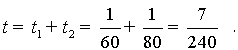 Средняя скорость на маршруте равна
Средняя скорость на маршруте равна
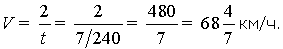 Двигаясь с этой скоростью, поезд пройдет путь от А до В за 7 часов, преодолев расстояние
Двигаясь с этой скоростью, поезд пройдет путь от А до В за 7 часов, преодолев расстояние 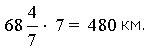 Способ 3.
Предположим, что задача решается в целых числах (т.е. искомое расстояние АВ и продолжительность движения в каждом из направлений – целые числа).
В этом случае расстояние АВ должно быть кратно каждой из двух скоростей.
Кроме того, расстояние АВ больше, чем 60 · 7 = 420 км (на движение с грузом поезд потратил более половины общего времени) и меньше, чем 80 · 7= 560 км (возвращение порожняком заняло менее половины времени, затраченного на всю поездку).
Единственное число, отвечающее приведенным условиям – 480. Искомое расстояние – 480 км/ч.
Справедливость сделанного предположения проверим, определив длительность поездки: 480:60+480:80=14 ч.
Найденное решение – единственное: изменение расстояния АВ приведет к изменению продолжительности движения*.
*Если в основу решения задачи положено некоторое предположение, проверка единственности решения необходима.
Способ 3.
Предположим, что задача решается в целых числах (т.е. искомое расстояние АВ и продолжительность движения в каждом из направлений – целые числа).
В этом случае расстояние АВ должно быть кратно каждой из двух скоростей.
Кроме того, расстояние АВ больше, чем 60 · 7 = 420 км (на движение с грузом поезд потратил более половины общего времени) и меньше, чем 80 · 7= 560 км (возвращение порожняком заняло менее половины времени, затраченного на всю поездку).
Единственное число, отвечающее приведенным условиям – 480. Искомое расстояние – 480 км/ч.
Справедливость сделанного предположения проверим, определив длительность поездки: 480:60+480:80=14 ч.
Найденное решение – единственное: изменение расстояния АВ приведет к изменению продолжительности движения*.
*Если в основу решения задачи положено некоторое предположение, проверка единственности решения необходима.
|
| Задача 2. Бесплатный хлеб в ресторане |
  В ресторане посетитель может съесть определенное количество ломтиков хлеба бесплатно. Но за каждый следующий ломтик надо уже платить.
Два человека вместе съели 13 ломтиков хлеба и заплатили 3 доллара.
Если такое же количества хлеба съел бы один человек, он бы должен был заплатить 8 долларов.
Сколько ломтиков хлеба может съесть один посетитель бесплатно? В ресторане посетитель может съесть определенное количество ломтиков хлеба бесплатно. Но за каждый следующий ломтик надо уже платить.
Два человека вместе съели 13 ломтиков хлеба и заплатили 3 доллара.
Если такое же количества хлеба съел бы один человек, он бы должен был заплатить 8 долларов.
Сколько ломтиков хлеба может съесть один посетитель бесплатно?
|
Решение.
Мы с другом договорились ходить каждый день в ресторан, где дают немного бесплатного хлеба.
В первый день мы съели 13 кусков хлеба и заплатили 3$.
На следующий день я пришел первым в ресторан и заказал 13 кусков хлеба, но друг не пришел, и мне пришлось заплатить не 3$, а 8$.
Значит, подумалось мне, то, что мог съесть мой друг бесплатно хлеба стоит 8$-3$=5$.
На следующий день повторилось то же самое. Я пришел первым, заказал хлеб, друга нет и еще официант сказал мне, что бесплатный хлеб отменили (из-за кризиса, наверно).
Значит, мне придется заплатить уже не 8$,как вчера, а плюс еще 5$ за свою "бесплатную" когда-то порцию хлеба.
Итого 8$+5$=13$ за 13 ломтиков хлеба, или 1$ за 1 ломтик.
Сколько ломтиков хлеба было в "бесплатной" порции узнаем, если разделим стоимость этой порции 5$ на стоимость одного ломтика 1$ = 5 ломтиков хлеба.
| <== предыдущая | | | следующая ==> |
| Техника выполнения измерения АД | | | Развитие способностей 1 page |
Date: 2015-07-01; view: 574; Нарушение авторских прав