Поверхности второго порядка. Метод сечений

Определение. Поверхностью второго порядка называется множество всех точек пространства, координаты которых в какой-либо аффинной системе координат удовлетворяют алгебраическому уравнению второй степени: 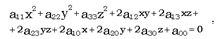(1) где – действительные числа, причем не все коэффициенты при членах второй степени равны нулю. В изучении поверхностей второго порядка мы не будем исследовать уравнение (1) поверхности, а рассмотрим основные типы поверхностей, используя их простейшие (канонические) уравнения. При этом мы будем использовать метод сечений, сущность которого состоит в следующем. Пусть поверхность S задана в прямоугольной системе координат уравнением F(x,y,z)=0. Поверхность S пересекаем плоскостями, параллельными координатным плоскостям (или самими координатными плоскостями), и находим линии пересечения поверхности с этими плоскостями. По виду этих линий и выносится суждение о форме поверхности S. Применение метода сечений основано на следующей теореме. Определение. Линия в пространстве ­– множество точек, принадлежащих двумерным поверхностям ψ и φ: 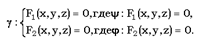Примером линии может служить прямая, заданная пересечением двух плоскостей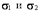

Прямолинейные образующие поверхностей второго порядка Определение. Прямая, лежащая на поверхности, называется прямолинейной образующей этой В поверхности. Рассмотрим вопрос о том, имеют ли прямолинейные образующие изученные выше поверхности II порядка. 1.Так КАК эллипсоид - фигура ограниченная, заключенная в параллелепипеде 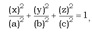то он не имеет прямолинейных образующих. 2. Рассмотрим двуполостный гиперболоид 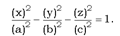Изучая ЕГО методом сечений (см. Глава 11, § 107), было выяснено, что сечение поверхности плоскостью г = ч при любом ч не содержит прямых линий. Поэтому гиперболический параболоид не имеет прямолинейных образующих, параллельных плоскости или лежащих в этой В плоскости. Если прямая не параллельна, не лежит в ней, то такая прямая пересекает плоскость г = ч в некоторой точке, которая не лежит на нашей поверхности, так как двуполостный гиперболоид не имеет общих точек с. Следовательно, на нашей прямой есть точки, не принадлежащие поверхности, и поэтому такая прямая не может быть прямолинейной образующей двуполостного гиперболоида. 3. Аналогично можно показать, ЧТО у эллиптического параболоида нет Добро прямолинейных образующих. 4. Прямолинейные образующие однополостного гиперболоида

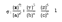(1)

напоминают уравнение однополостного гиперболоида. Преобразуем его: 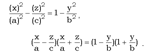(1 ')

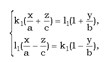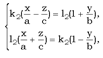Рассмотрим две системы уравнений: (2) (3)

где,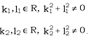

.

Легко подсчитать, что в каждой из систем уравнений (3), (4) ранг матрицы, составленной из коэффициентов при х, у, г равен двум, то есть системы (3), (4) определяют прямую при фиксированных 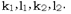Заметим, ЧТО если координаты некоторой Точки удовлетворяют Любой из Систем уравнений (3), (4) (при фиксированных), то они удовлетворяют уравнению (1 '), а значит и (1), то есть 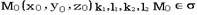. Обратное тоже верно. То есть прямые, определяемые системами (3), (4) есть прямолинейные образующие однополостного гиперболоида. Системы (3) и (4) ПРИ различных определяют Два семейства прямолинейных образующих. 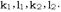Свойства прямолинейных образующих однополостного гиперболоида. 1. Через каждую точку однополостного гиперболоида проходят две и только две прямолинейные образующие. Одна из них принадлежит семейству (3), а другая (4). 2. Любые две прямолинейные образующие одного семейства скрещиваются. 3. Любые две прямолинейные образующие из разных семейств лежат в одной плоскости. 4. Прямолинейные образующие гиперболического параболоида. Напомним, что уравнение гиперболического параболоида имеет вид: 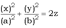(5)или 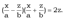(5 ') Рассмотрим 2 системы: 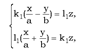(6) 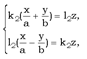(7) где, 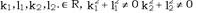. Аналогично, однополостному гиперболоиду системы (6) и (7) определяют два семейства прямолинейных образующих гиперболического параболоида. Замечание. Прямолинейные образующие гиперболического параболоида обладают свойствами 1 - 3., аналогичные свойствам однополостного гиперболоида. Пример. Найти прямолинейные образующие однополостного гиперболоида 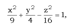проходящие через точку 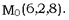Решение. Запишем уравнение в виде (1 '). .Для 1 семейства имеем: 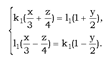(*) Подставляя в (*) х = 6, у = 8, получим 2, то есть можно, например, взять 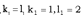.Подставляя эти значения в систему (*), имеем: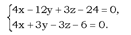

Эти уравнения определяют прямолинейные образующие, проходящие через точку И принадлежащие 1 семейству 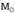. Аналогично системе (3) получили прямолинейные образующие 2 семейства, проходящие через точку .

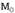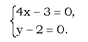
21.

Отображения и преобразования множеств. Композиция преобразований. Примеры преобразований плоскости. Опр. Пусть X,Y – множества. Говорят, что задано отображение f множества X Y, если каждому элементу x X поставлен в соответствие единственный элемент y Y(обозн. f:X Y или X Y). Элемент x – прообраз элемента y при отображении f. у – образ x при f и обоз. y=f(x). Виды отображений. Опр. Отображение f:X Y наз. Инъективным или инъекцией, если образы различных элементов множества X различны( x, 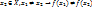). Обозначим f(x) множества X. f(x)={f(x) 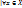} – образ множества X. Опр. Отображение f: X 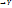наз. сюрьективным, сюрьекцией если f(x)=Y (отображение «на»). Опр. Отображение f:X Y наз. Биективным или взаимно-однозначным если оно одновременно инъективно и сюрьективно. Опр. Отображение 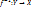наз. обратным для отображения f:X Y если оно действует по закону: 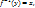если y=f(x). Отображение наз. обратимым если для него сущ-ет обратное отображение. Не всякое отображение обратимо. Биекции всегда обратимы. Опр. Преобразованием множества X наз. биективное отображение f:X X. Опр. Преобразование множества наз-ся тождественным, если оно в каждой точке множества ставит в соответствие саму эту точку (e: X X, 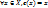). Опр. Обратимым преобразованием для преоб. f:X X наз-ся преоб. 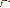, которое 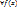ставит в соответствие элемент x. Если на множ-ве X заданы два преобразования 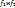, , ставит в соответствие (x) 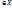, то говорят, что 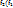(x) 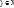получен из в результате композиции преобразований 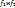( 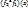= 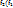(x) читают в обратном порядке).

22.

Группа преобразований. Теор.1 Пусть f – преобразование множества X, 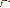– обратное преобр-е. Тогда 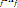= e (тождественное). Теор.2 Композиция преобразований обладает свойством ассоциативности (). Опр. Множество G преобразований мн-ва X наз-ся группой преобразований если выполняются условия: 1) Для двух преобразований из мн-ва G их композиция также принадлежит G. 2) Для преобразования из G, обратное преобразование также принадлежит G. Теор.3 Группа преобразований G множества X всегда содержит тождественное преобразование множества X.(e G). Примеры групп преобразований: 1) X - множество, G={e}(тождественное преобразование множества X) тогда G – группа преобразований (тривиальная группа преобразований). 2) X - множество, G – содержит все преобразования мн-ва X, тогда G – группа преобразований. Опр. Подмножество H группы G преобразований наз-ся подгруппой если Н – группа преобразований.

23.

Движения плоскости и их свойства. Аналитическое выражение движения. Опр. Преобразования F плоскости наз-ся движением плоскости, если оно сохраняет расстояние между точками, т.е A,B (A,B)= (F(A), F(B)). Рассмотрим на плоскости два ортонормированных рипера: R={0, }, ={ 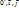}. Зададим отображение, которое в M 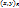ставит в соответствие 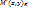(обозн. F). Построенное отображение биективно, поэтому явл-ся преобразованием плоскости. Далее мы доказали, что оно также является движением. Найдем аналитическое выражение движения. Пусти переход от R к R’ осущ-ся по формулам: 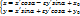(1), где 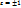;x,y – старые координаты некоторой точки, относ-но рипера R; x’,y’ – новые координаты той же точки относ-но R’. Пусть M 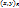- точка плоскости. При движении F, точка перейдет в точку F(M) 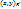. Обозначим старые координаты т. F(M) 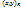. Применим к т. F(M) формулы (1): 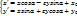(2), где 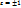. Формулы (2) выражают связь между координатами x,y т. М отн-но R и координатами x’,y’ т. F(M) отн-но R. Получили связь между координатами т. прообраза и т. образа. Значит (2) – аналитическое выражение движения. Верно и обратное: преобразование плоскости, заданное в ортонормированном рипере формулами (2) есть движение. Движение сохраняет отношение «между». Св-ва движения: 1) При движении отрезок переходит в отрезок, прямая в прямую, луч в луч, полуплоскость в полуплоскость; 2) Движение сохраняет простое отношение 3-ч точек; 3) Движение сохраняет параллельность прямых.

24.

Симметрия относительно прямой. Параллельный перенос. Опр. Пусть на плоскости дана прямая L. Отображение, которое т. M плоскости ставит в соответствие т. M’ этой плоскости, так что выполняются условия: 1)MM’ ; 2)MO=MO’, где O=MM’ наз-ся осевой симетрией. Нами получено отображение плоскости на себя, которое явл-ся биекцией. Т.е мы получили преобразование плоскости 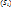ось симетрии. Найдем аналитическое выражение движения. В качестве оси симетрии выберем ось Оx. 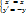(3) – аналитическое выражение осевой симетрии с осью Ох. 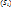также является движением. Опр. Выберем 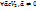. Поставим в соответствие т. 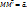M плоскости M’ плоскости, т.ч Это параллельный перенос на вектор (обозн-ся ). 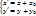(4) –аналитическое выражение . detA=1, A – ортогональна 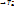– движение. Будем считать тождественное преобразование плоскости параллельным переносом на нулевой вектор (E= ). Теор. Множество всех параллельных переносов плоскости образует группу. Теор. Композиция 2-х отражений от 2-х параллельных прямых есть параллельный перенос. Справедливо и обратное.

25.

Поворот с данным центром. Центральная симметрия. Скользящая симметрия. Опр. Пусть на плоскости выбрана точка О – центр поворота и выбран ориентированный угол , причем 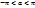. Поставим в соответствие каждой точке M(М 0) плоскости точку M’, т.ч выполнялись условия: 1) 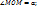2) 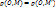. Полученное преобразование плоскости наз-ся поворотом вокруг центра О на угол и обозначается . M(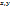) поставим в соответствие M’(x’,y’). Рассмотрим полярную сис-му координат (0, ), M(r, ), M’(r, 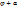). 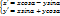(5) – аналитическое выражение поворота плоскости с данным центром на 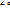. 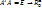– движение плоскости. Опр. Центральной симетрией наз-ся поворот вокруг точки на угол (обозн-ся 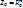). E= . Теор. Множество всех поворотов вокруг т. О образует группу. Теор. Композиция 2-х отражений от 2-х отображений от 2-x пересекающихся прямых есть поворот с центром в т. пересечения этих прямых. 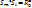, 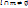. Верно и обратное. Опр. Пусть на плоскости дана прямая и выбран вектор . 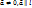Рассмотрим композицию движений 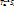.Полученное отражение плоскости наз-ся скользящей симетрией. 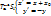(6) – аналитическое выражение скользящей симетрии. 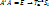– движение. Скользящую симетрию можно представить в виде композиций осевых симетрий: 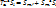; где m .

26.

Опр. если репер Rи R’определ. движение F ориентированы одинаково, тоF называется движением I рода; если же Rи R’ ориентированы противоположно то F движение 2 рода. 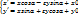(1) Формулы движения (1)определены движением 1 рода при 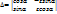= И движения второго рода при 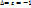. Первый род-параллельный перенос, поворот центральной симметрии, тождественные преобразования. второй род-осевая и скользящая симметрия.

Опр. точка М плоскости называется инвариантной или неподвижной точкой движения F,если F(M)=M. Классификация движения по количеству инвариантных точек:

1) Пусть F движение 1-го рода, т.е.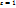

(2)

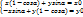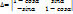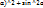
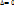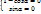(3) система линейных алгебраических переменных(СЛАУ).Все решения этой системы явл. Инвариантными точками движения F. =(1-cos ó 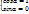ó ó 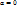. Подставим 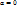в формулу(1). 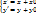формулы параллельного переноса 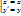тождественное преобразование плоскости Т.1)В любое движение первого рода есть либо параллельный перенос либо поворот вокруг точки на угол ,либо (тождественное преобразование) 2)ПустьF движение второго рода ( для классификации движения 2-го рода удобно искать неинвариантные точки преобразования, а инвариантные векторы. Т2 любое движение второго рода есть либо осевая симметрия либо скользящая симметрия. Классификация движения:

1. 1-го рода:

1.1. Паралл. Перенос;

1.2. Поворот:

· Тождественное преобразование

· Центральная симметрия

2. 2-го рода

2.1. Скользящая симметрия

2.2. Осевая

Теорема: любое движение плоскости может быть представлено в виде композиции не более чем 3-х осевых симметрий.

28.