
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Различные способы задания прямой в пространстве
|
|
Прямая определена точкой.
M  d ↔ M0M = at (1)
d ↔ M0M = at (1)
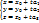 где t
где t  R параметрическое уравнение прямой (2)
R параметрическое уравнение прямой (2)
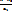 =
= 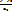 =
= 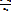 (a1 ≠0; a2 ≠0; a3 ≠0) каноническое уравнение прямой (3)
(a1 ≠0; a2 ≠0; a3 ≠0) каноническое уравнение прямой (3)
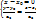 уравнение прямой в виде пересечения двух плоскостей (4)
уравнение прямой в виде пересечения двух плоскостей (4)
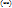
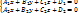 где r(A) =
где r(A) = 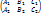 = 2(*)
= 2(*)
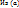 выч пересечение
выч пересечение
A1x0 + B1y0 + C1z0 = 0 (6)
Из (a) - (6)
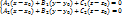
x-x0 = 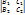 t с одной стороны это векторное произведение, а с другой
t с одной стороны это векторное произведение, а с другой
y-y0 = 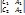 t координат направляющ вектором
t координат направляющ вектором
z-z0 = 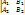 t
t
Векторное произведение – направляющий вектор плоскости.
Если n1*n2 =  -каждая координата равна
-каждая координата равна
10.
Взаимное расположение прямой и плоскости
Возможны три варианта взаимного расположения прямой и плоскости
1. Прямая параллельна плоскости, если она не имеет с плоскостью общих точек. На левом
рисунке прямая l параллельна плоскости pi.
2. Прямая пересекает плоскость, если она имеет с плоскостью ровно одну общую точку. На рисунке в центре прямая l пересекает плоскость pi в точке A.
3. Прямая лежит в плоскости, если каждая точка прямой принадлежит этой плоскости. На
правом рисунке прямая l лежит в плоскости pi. В таком случае говорят ещё, что плоскость
pi проходит через прямую l.

Взаимное расположение двух прямых и пространстве характеризуется следующими тремя возможностями.
1.Прямые лежат в одной плоскости и не имеют общих точек — параллельные прямые.
2.Прямые лежат и одной плоскости и имеют одну общую точку — прямые пересекаются.
3.В пространстве две прямые могут быть расположены еще так, что не лежат ни в одной плоскости. Такие прямые называются скрещивающимися (не пересекаются и не параллельны).
Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая пересекает эту плоскость и точке, которая не лежит на первой прямой, то эти прямые скрещиваются.
Теорема. Через каждую из двух скрещивающихся прямых проходит только одна плоскость, параллельная другой прямой.
Примеры скрещивающихся прямых: трамвайный рельс и троллейбусный провод по пересекающейся улице, нeпересекающиеся и непараллельные ребра пирамид или призм и пр. Все три случая можно видеть еще на примере прямых, по которым встречаются стены и потолок или стены и пол комнаты.
12)
Поверхности второго порядка. Цилиндрические поверхности второго порядка. Цилиндрические ПВП, направляющими которых служат ЛВП. Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению вида 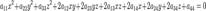 в котором по крайней мере один из коэффициентов
в котором по крайней мере один из коэффициентов 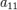 ,
, 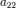 ,
, 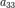 ,
, 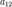 ,
, 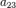 ,
, 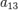 отличен от нуля. Типы поверхностей второго порядка 1 Цилиндрические поверхности; 2 Конические поверхности; 3 Поверхности вращения; 4 Эллиптический параболоид; 5 Гиперболический параболоид; 6 Центральные поверхности
отличен от нуля. Типы поверхностей второго порядка 1 Цилиндрические поверхности; 2 Конические поверхности; 3 Поверхности вращения; 4 Эллиптический параболоид; 5 Гиперболический параболоид; 6 Центральные поверхности
Поверхность  называется цилиндрической поверхностью с образующей
называется цилиндрической поверхностью с образующей 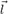 , если для любой точки
, если для любой точки 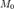 этой поверхности прямая, проходящая через эту точку параллельно образующей
этой поверхности прямая, проходящая через эту точку параллельно образующей 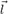 , целиком принадлежит поверхности
, целиком принадлежит поверхности  . Теорема (об уравнении цилиндрической поверхности). Если в некоторой декартовой прямоугольной системе координат поверхность
. Теорема (об уравнении цилиндрической поверхности). Если в некоторой декартовой прямоугольной системе координат поверхность  имеет уравнение
имеет уравнение 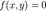 , то
, то  — цилиндрическая поверхность с образующей, параллельной оси
— цилиндрическая поверхность с образующей, параллельной оси 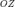 . Кривая, задаваемая уравнением
. Кривая, задаваемая уравнением 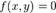 в плоскости
в плоскости  , называется направляющей цилиндрической поверхности. Поверхность, которая в некоторой декартовой системе координат задается уравнением
, называется направляющей цилиндрической поверхности. Поверхность, которая в некоторой декартовой системе координат задается уравнением 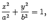
называется эллиптическим цилиндром, поверхность, которая задается уравнением 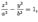
называется гиперболическим цилиндром, а которая задается уравнением
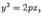 называется параболическим цилиндром.
13)
Конические ПВП
Поверхность называется параболическим цилиндром.
13)
Конические ПВП
Поверхность  называется конической поверхностью с вершиной в точке называется конической поверхностью с вершиной в точке  , если для любой точки , если для любой точки  этой поверхности прямая, проходящая через этой поверхности прямая, проходящая через 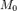 и и 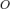 , целиком принадлежит этой поверхности. Функция , целиком принадлежит этой поверхности. Функция 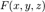 называется однородной порядка называется однородной порядка 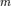 , если , если 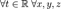 выполняется следующее: выполняется следующее:  Теорема (об уравнении конической поверхности). Если в некоторой декартовой прямоугольной системе координат поверхность Теорема (об уравнении конической поверхности). Если в некоторой декартовой прямоугольной системе координат поверхность  задана уравнением задана уравнением 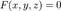 , где , где 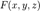 — однородная функция, то — однородная функция, то  — коническая поверхность с вершиной в начале координат. Если поверхность — коническая поверхность с вершиной в начале координат. Если поверхность  задана функцией задана функцией 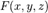 , являющейся однородным алгебраическим многочленом второго порядка, то , являющейся однородным алгебраическим многочленом второго порядка, то  называется конической поверхностью второго порядка. Каноническое уравнение конуса второго порядка имеет вид: называется конической поверхностью второго порядка. Каноническое уравнение конуса второго порядка имеет вид:
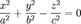
|
14)
Поверхности вращения второго порядка Определение. Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d, называется поверхностью вращения с осью вращения d.
Если уравнение поверхности в прямоугольной системе координат имеет вид:
F(x2 + y2, z) = 0, то эта поверхность – поверхность вращения с осью вращения Оz.
Аналогично: F(x2 + z2, y) = 0 – поверхность вращения с осью вращения Оу,
F(z2 + y2, x) = 0 – поверхность вращения с осью вращения Ох.
1) 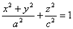 - эллипсоид вращения
- эллипсоид вращения
2) 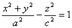 - однополостный гиперболоид вращения
- однополостный гиперболоид вращения
3) 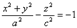 - двуполостный гиперболоид вращения
- двуполостный гиперболоид вращения
4) 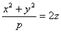 - параболоид вращения
- параболоид вращения
15)
Date: 2015-07-01; view: 700; Нарушение авторских прав