
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема3
|
|
Для линейной зависимости трех векторов необходимо и достаточно,чтобы эти векторы были компланарны.
Пусть векторы a, b, c линейно зависимы, тогда один из них линейно выражается через другие. Пусть c = αa + βb. Усли а и b коллиниарны, то а, b, с коллиниарны и, тем более, компланарны. Если a и b неколлинеарны, то отложим векторы a, b, c от одной точки (рис. 2, б). Тогда вектор с, являясь диагональю параллелограмма, построенного на векторах αa и βb, окажется в той же плоскости, что и a, b. Значит, a, b, c компланарны.
Достаточность. Пусть a, b, c компланарны, т.е. параллельны одной плоскости. Будем считать, что a, b неколлиниарны (так как если a, b коллиниарны, то линейная зависимость a, b, c следует из линейной зависимости подсистемы). Отложим a, b и с от одной точки. Тогда они окажутся в одной плоскости и на основании утверждения 2 будем иметь c = αa + βb. В силу теоремы 2.2 отсюда следует, что векторы a, b, c линейно зависимы.
Вопрос 5.
Векторы 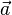 и
и  линейно зависимы тогда и только тогда, когда они коллинеарны (лежат на параллельных прямых).
линейно зависимы тогда и только тогда, когда они коллинеарны (лежат на параллельных прямых).
Векторы  линейно зависимы тогда и только тогда, когда они компланарны (лежат в одной плоскости).
линейно зависимы тогда и только тогда, когда они компланарны (лежат в одной плоскости).
6 вопрос.
Базисом в пространстве называются три некомпланарных вектора 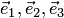 , взятые в определённом порядке (рис.1.32). Эти векторы
, взятые в определённом порядке (рис.1.32). Эти векторы 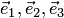 называются базисными.
называются базисными.
Пусть в пространстве задан базис 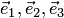 . Построим прямые
. Построим прямые 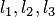 , содержащие базисные векторы
, содержащие базисные векторы 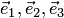 соответственно. Без ограничения общности можно считать, что эти прямые пересекаются в одной точке (в противном случае можно было взять любые пересекающиеся в одной точке прямые
соответственно. Без ограничения общности можно считать, что эти прямые пересекаются в одной точке (в противном случае можно было взять любые пересекающиеся в одной точке прямые  , параллельные прямым
, параллельные прямым 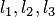 соответственно, поскольку проекции вектора на параллельные прямые равны. Тогда любой вектор
соответственно, поскольку проекции вектора на параллельные прямые равны. Тогда любой вектор 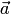 можно однозначно представить в виде суммы своих проекций:
можно однозначно представить в виде суммы своих проекций: 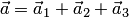 , где
, где 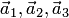 — векторы, принадлежащие прямым
— векторы, принадлежащие прямым 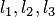 соответственно (см. п.2 теоремы 1.1). Раскладывая проекции
соответственно (см. п.2 теоремы 1.1). Раскладывая проекции 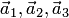 по базисам на соответствующих прямых (см. разд.1.3.1), находим:
по базисам на соответствующих прямых (см. разд.1.3.1), находим:  . Подставляя эти разложения в равенство
. Подставляя эти разложения в равенство 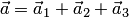 , получаем
, получаем
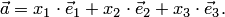
| (1.4) |
Таким образом, справедлива следующая теорема.
Теорема 1.5 (о разложении вектора по базису в пространстве). Любой вектор 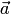 может быть разложен по базису
может быть разложен по базису 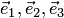 в пространстве, т.е. представлен в виде (1.4), где числа
в пространстве, т.е. представлен в виде (1.4), где числа 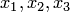 определяются однозначно.
определяются однозначно.
Коэффициенты 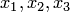 в разложении (1.4) называются координатами вектора
в разложении (1.4) называются координатами вектора 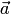 относительно базиса
относительно базиса 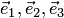 (число
(число 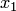 , называют абсциссой,
, называют абсциссой,  — ординатой, а
— ординатой, а 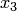 — аппликатой вектора
— аппликатой вектора 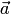 ). Например, числа
). Например, числа 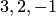 являются координатами вектора
являются координатами вектора 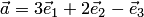 (
( — абсцисса,
— абсцисса,  — ордината,
— ордината,  — аппликата вектора
— аппликата вектора 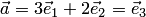 ).
).
Базисные векторы 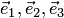 , отложенные от одной (произвольной) точки, называются репером.
, отложенные от одной (произвольной) точки, называются репером.
7 вопрос.
Векторы называются компланарными, если они принадлежат одной или параллельным плоскостям.
Два вектора 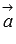 и
и  трехмерного пространства всегда компланарны.
трехмерного пространства всегда компланарны.
необходимое и достаточное условие компланарности трех векторов в пространстве.
Для компланарности трех векторов  и
и  трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
Доказательство.
Пусть 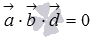 , докажем что векторы
, докажем что векторы  и
и  компланарны.
компланарны.
Так как 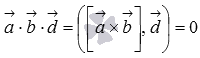 , то векторы
, то векторы 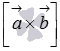 и
и  перпендикулярны в силу необходимого и достаточного условия перпендикулярности двух векторов. С другой стороны, по определению векторного произведения вектор
перпендикулярны в силу необходимого и достаточного условия перпендикулярности двух векторов. С другой стороны, по определению векторного произведения вектор 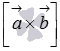 перпендикулярен и вектору
перпендикулярен и вектору 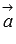 и вектору
и вектору  . Следовательно, векторы
. Следовательно, векторы  и
и  компланарны, так как перпендикулярны одному вектору
компланарны, так как перпендикулярны одному вектору 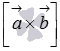 .
.
8 вопрос.
Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Если хотя бы один из двух векторов нулевой, то угол между ними не определён, а скалярное произведение считается равным нулю. (написать в ручную)
где  — величина угла между векторами
— величина угла между векторами 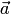 и
и 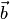 .
.
Скалярное произведение вектора самого на себя  называется скалярным квадратам.
называется скалярным квадратам.
Свойства.
Свойства скалярного произведения:
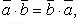 переместительный закон
переместительный закон
 сочетательное свойство
сочетательное свойство
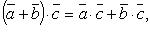 распределительное свойство.
распределительное свойство.
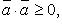
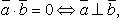
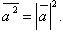 скалярный квадрат равен квадрату его длины
скалярный квадрат равен квадрату его длины
9 вопрос.
Векторное произведение
Векторное произведение векторов 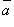 и
и 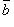 - вектор, обозначаемый
- вектор, обозначаемый 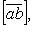
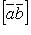 или
или  для когорого:
для когорого:
1)  (
( - угол между векторами
- угол между векторами 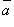 и
и 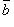 ,
,  );
);
2) 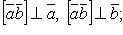
3) тройка 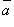 ,
, 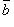 ,
, 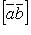 - правая.
- правая.
Свойства векторного произведения:
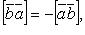
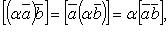

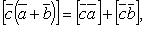
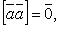
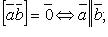
если 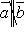 , то
, то 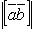 равен площади параллелограмма, построенного на приведенных к общему началу векторах
равен площади параллелограмма, построенного на приведенных к общему началу векторах 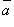 и
и 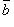 .
.
10 вопрос.
Теорема. Пусть 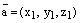 ,
, 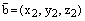 ,
, 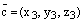 . Тогда:
. Тогда:
1) 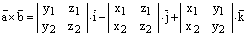 ;
;
2) 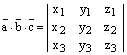 .
.
Доказательство. 1) Используем свойство линейности векторного произведения:

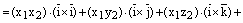

 .
.
Далее, заметим, что векторные произведения коллинеарных векторов равны нулевому вектору:
 .
.
Рассмотрим другие векторные произведения базисных векторов:

рис.4.
 ,
,  ,
,  .
.
Эти равенства легко устанавливаются с помощью рис.4.
Отсюда следует: 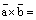
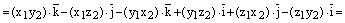
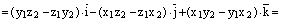
 , ч.т.д.
, ч.т.д.
2) Воспользуемся только что доказанной формулой:
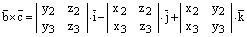 .
.
Теперь, по теореме о скалярном произведении векторов в координатной форме, получаем:
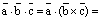
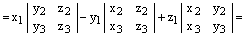
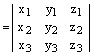 , ч.т.д.
, ч.т.д.
Date: 2015-07-01; view: 407; Нарушение авторских прав