Метод барьеров и метод центров

Идейно близкими к методу штрафов являются метод барьеров и метод центров. В них

также последовательность приближений к решению задачи на условный минимум строится путем решения последовательности задач на безусловный минимум. Однако минимизируемые функции в них определяются так, что последовательность приближений находится внутри допустимой области. Поэтому эти методы иногда называют методами внутренней точки. Коротко остановимся на этих методах.

Определение 1. Пусть 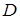– некоторое множество из 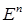, предположим, что его внутренность не пуста. Функцию 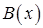, определенную на 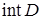, назовем барьерной функцией для множества 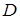, если 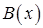положительна на 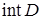и неограниченно возрастает при стремлении 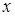к границе множества .

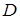Приведем примеры барьерных функций. Пусть 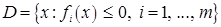, где 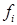– непрерывные функции, определенные на 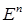, система неравенств, задающая 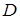, удовлетворяет условию Слейтера. Барьерные функции для такого множества можно задать, например, следующим образом:

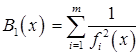и .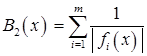

Пусть имеется задача на отыскание условного минимума функции 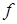на множестве 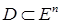. Определим на 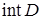следующую функцию:

,

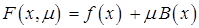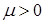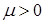
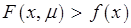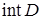где . Легко увидеть, что из определения барьерной функции следует, что при любом на и 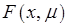неограниченно возрастает при стремлении 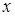к границе множества .

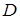Далее, при фиксированном положительном 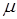поставим задачу

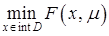. (1)

Предположим, что задача (1) имеет решение. Обозначим через 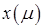точку минимума функции .

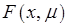Если задача на условный минимум удовлетворяет ряду требований, то 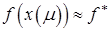при достаточно малых положительных значениях параметра 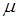, а точка 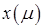может быть достаточно близка к множеству 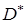. На этом свойстве основаны численные алгоритмы метода барьеров.

Пусть последовательность ,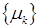

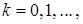
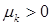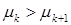
такова, что , 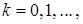и 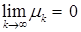. Обозначим 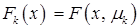, 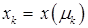. Таким образом, для построения последовательности приближений 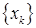, 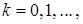решается последовательность задач

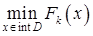. (2)

Итак, все точки 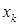принадлежат внутренности допустимого множества и 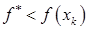для всех 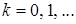, то есть приближение к решению происходит изнутри множества 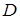, а приближение к 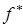осуществляется сверху.

Имеет смысл строить одновременно две последовательности, а именно – одну последовательность генерировать методом штрафных функций, а другую – методом барьерных функций. Это позволит приближаться к 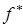сверху и снизу одновременно.

В заключение этого параграфа коротко остановимся на методе центров.

Пусть необходимо решить задачу на отыскание условного минимума функции 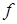на множестве 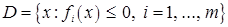. Обозначим через 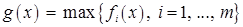. Легко увидеть, что тогда 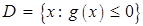. Пусть 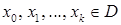. Для нахождения приближения 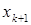решаем задачу ми-

нимизации так называемой функции d-рассто-яния :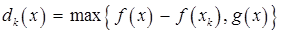

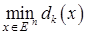(3)

Точку 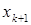называют центром множества

.

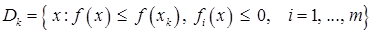Отсюда и название метода.

Существуют различные модификации этого метода. Например, для нахождения центра мно-жества 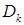используются другие функции. В некоторых модификациях после решения задачи (3) дополнительно осуществляется одномерный поиск.

Заметим, что, несмотря на кажущуюся простоту метода центров, в его реализации возникают определенные трудности, связанные, в первую очередь, с недифференцируемостью целевой функции в задаче (3). Возможные подходы к минимизации недифференцируемых функций мы обсудим в следующем параграфе.

Date: 2015-06-12; view: 816; Нарушение авторских прав