
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Симплексный метод
|
|
Метод последовательного улучшения плана является принципиальной схемой решения задач линейного программирования, основанной на целенаправленном переборе допустимых базисов. В методе последовательного улучшения плана не конкретизированы способы решения систем ли-нейных алгебраических уравнений в пунктах 1 и 4, а также остается открытым вопрос об отыскании исходного допустимого базиса и соответствующего ему опорного плана. На основе метода последовательного улучшения плана созданы различные численно реализуемые методы (алгоритмы). Одним из них является симплексный метод.
Введем так называемую симплексную таблицу 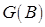 , представляющую собой матрицу размерности
, представляющую собой матрицу размерности 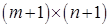 , которая однозначно определяется по базису
, которая однозначно определяется по базису 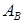 следующим образом:
следующим образом:
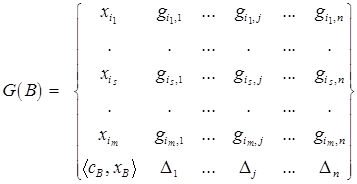 .
.
Значения 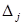 в этой матрице вычисляются по формулам
в этой матрице вычисляются по формулам 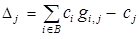 , полученным в теореме 1 параграфа 2.
, полученным в теореме 1 параграфа 2.
Симплексная таблица содержит всю необходимую информацию для осуществления итерации метода последовательного улучшения плана. Заметим, что вычисление базисных координат опорного решения 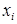 и коэффициентов
и коэффициентов 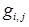 по определению (то есть путем решения систем линейных уравнений) довольно трудоемко и осуществляется только один раз на начальном шаге метода. В дальнейшем при переходе от данного базиса к следующему (от одной итерации метода к следующей) симплексная таблица пересчитывается по сравнительно простым правилам, основанным на методе исключения. Формулы пересчета симплексной таблицы получены в следующей теореме.
по определению (то есть путем решения систем линейных уравнений) довольно трудоемко и осуществляется только один раз на начальном шаге метода. В дальнейшем при переходе от данного базиса к следующему (от одной итерации метода к следующей) симплексная таблица пересчитывается по сравнительно простым правилам, основанным на методе исключения. Формулы пересчета симплексной таблицы получены в следующей теореме.
Теорема 1. Пусть 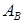 и
и 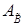 – допустимые базисы, где
– допустимые базисы, где 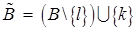 , значения индексов
, значения индексов 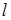 и
и
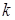 получены по правилам метода последовательного улучшения плана,
получены по правилам метода последовательного улучшения плана, 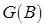 и
и 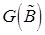 – соответствующие этим базисам симплексные таблицы. Тогда для элементов симплексной таблицы
– соответствующие этим базисам симплексные таблицы. Тогда для элементов симплексной таблицы 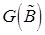 справедливы следующие равенства:
справедливы следующие равенства:
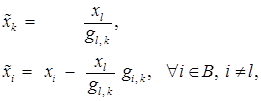 (1)
(1)
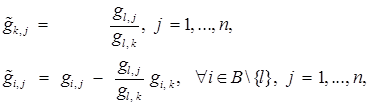 (2)
(2)
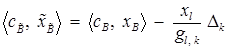 , (3)
, (3)
 (4)
(4)
Доказательство. Формулы (1) и (3) получены ранее (см. формулы (8) и (10) параграфа 2).
Обоснуем равенства (2). Из разложения век-
тора 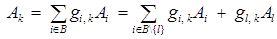 выразим
выразим
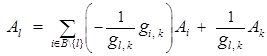 . (5)
. (5)
Выберем произвольно 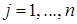 и в разложение
и в разложение
вектора 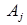 подставим (5). Получим
подставим (5). Получим
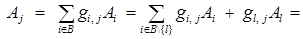
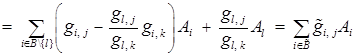 .
.
Откуда и следуют формулы (2).
Далее убедимся в справедливости равенств (4). Выберем произвольно 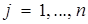 . Тогда
. Тогда
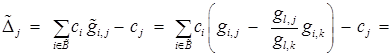

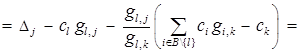
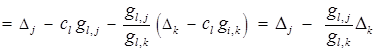 .
.
Что и требовалось.
Теперь мы можем сформулировать симплексный метод. Выберем некоторый допустимый базис 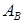 . Далее выполняются следующие действия:
. Далее выполняются следующие действия:
0._Построение исходной симплексной таблицы 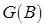 (этот этап осуществляется только один раз до начала выполнения первой итерации).
(этот этап осуществляется только один раз до начала выполнения первой итерации).
1._Проверка признака оптимальности
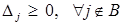 . (6)
. (6)
Если все неравенства (6) выполняются, то 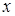 – решение задачи, и метод прекращает работу.
– решение задачи, и метод прекращает работу.
2._Выбор  . Положим
. Положим 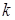 :
: 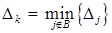 .
.
3._Построение 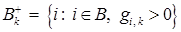 .
.
4._Если 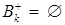 , то задача не имеет решения в силу неограниченности целевой функции на допустимом множестве. Работа метода прекращается.
, то задача не имеет решения в силу неограниченности целевой функции на допустимом множестве. Работа метода прекращается.
5._Выбор 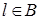 . Найдем номер
. Найдем номер 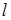 такой, что
такой, что
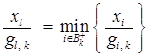 .
.
6._Построение нового базиса 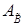 , где
, где 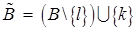 .
.
7._Пересчет симплексной таблицы по формулам (1) – (4).
8._ Переход к следующей итерации, к первому ее этапу.
| <== предыдущая | | | следующая ==> |
| Стилизованная рамка для зеркала | | | Программа. Директор по логистике филиала Уральский |
Date: 2015-06-12; view: 415; Нарушение авторских прав