Криптосистема заснована на еліптичних кривих

У 1985 році Коблиць і Міллер незалежно друг від друга зпропонували використовувати для побудови криптосистем алгебраїчні структури, визначені на безлічі крапок на еліптичних кривих. Розглянемо випадок визначення еліптичних кривих над простими кінцевими полями довільної характеристики і над полями Галуа характеристики 2.

Нехай 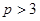– просте число. Нехай 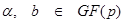такі, що 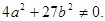Еліптичної кривої над полем 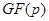називається безліч рішень 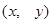рівняння

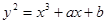
над полем 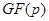разом з додатковою крапкою 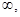названою крапкою в нескінченності.

Представлення еліптичної кривої у виді рішення зветься еліптичною кривою у формі Вейерштрасса.

Позначимо кількість крапок на еліптичної кривої через ﭕ# . Верхня і нижня границі для # визначаються теоремою Хассе:

# .

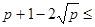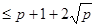Задамо бінарну операцію на (в адитивному запису) наступними правилами:

(I) ;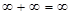

(II) ;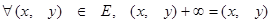

(III) ;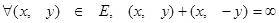

(IV) ,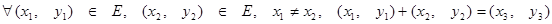

де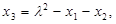

.

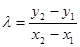(V) ,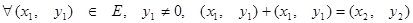

де

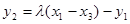
Безліч крапок еліптичної кривої із заданої в такий спосіб операцією утворить абелеву групу.

Якщо # = 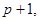то крива називається суперсигулярною.

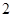Еліптична на є суперсигулярною кривою над полем характеристики та задається в такий спосіб. Нехай 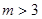- ціле число. Нехай 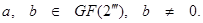Еліптичної кривої над полем 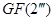називається безліччю рішень 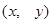рівняння

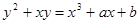
над полем разом з додатковою крапкою 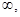названою крапкою в нескінченності.

Кількість крапок на кривій також визначається теоремою Хассе:

# .

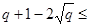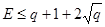де 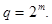Більш того, # четно.

Операція додавання на у цьому випадку задається наступним правилами:

(I) ;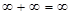

(II) ;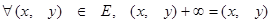

(III)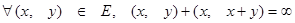

(IV) ,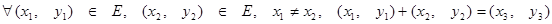

де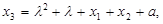

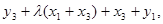
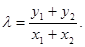
(V)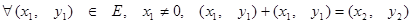

де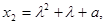

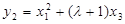
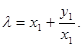
У цьому випадку безліч крапок еліптичної кривої із заданої в такій спосіб операцією також утворить абелеву групу.

Користуючись операцією додавання крапок на кривої, можна природним образом визначити операцію множення крапки 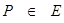на довільне ціле число :

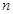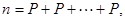
де операція додавання виконується 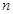раз.

Тепер побудуємо однобічну функцію, на основі якої можна буде створити криптографічну систему.

Нехай – еліптична крива, 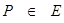– крапка на цій кривій.Вибиремо ціле число 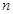< # . Тоді як пряму функцію виберемо добуток 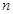. Для його обчислення по оптимальному алгоритму буде потрібно не менше 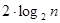операцій додавання. Зворотну задачу сформулюємо в такий спосіб: по заданій еліптичної кривої , крапці 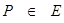і добутку 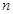знайти 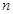. В даний час усі відомі алгоритми рішення цієї задачі вимагають експонентного часу.

Для встановлення захищеного зв’язку два користувача 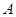і 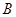спільно вибирають еліптичну криву і крапку 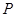на ній. Потім кожен з користувачів вибирає своє секретне ціле число, відповідно 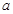і 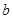. Користувач 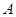обчислює добуток 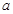, а користувач 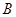– 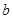.Далі вони обмінюються обчисленими значеннями При цьому параметри самої кривої, координати крапки на ній і значення добутків є відкритими і можуть передаватися по незахищених каналах зв’язку.

Потім користувач 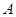множить отримане значення на 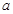, а користувач 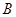множить отримане їм значення на 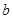. У силу властивостей операції множення на число 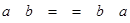. Таким чином, обоє користувача одержать загальне секретне значення (координати крапки 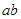), що вони можуть використовувати для одержання ключа шифрування. 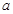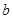Відзначимо, що зловмиснику для відновлення ключа буде потрібно вирішити складну з обчислювальної точки зору задачу визначення і по відомим 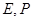, 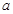і .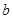

Різні способи використання криптографії описано нижче.

1. Безпека конфіденційності даних

В обставинах, коли важливо зберігати конфіденційність, тобто коли інформація є надзвичайно чутливою, треба розглядати засоби безпеки, що зашифровують інформацію для зберігання чи передавання мережею. Під час вирішення питання про використання засобів шифрування треба брати до уваги:

– відповідні державні закони та норми;

– вимоги до керування ключами та труднощі, які треба подолати для гарантування того, що справжні поліпшення безпеки досягаються без створення нових вразливостей, та

– прийнятність використовування механізмів шифрування для розгортання та рівень необхідної безпеки.

2. Безпека цілісності даних

За обставин, коли важливим є цілісність даних, що зберігаються чи оброблюються, для безпеки цих даних треба розглянути геш-функції, цифрові підписи та (або) засоби забезпечення цілісності. Засоби безпеки цілісності надають безпеку від випадкової чи зловмисної зміни, долучення чи вилучення інформації. Засоби цифрових підписів можуть забезпечувати безпеку, схожу до засобів цілісності повідомлень, але також мають властивості, що дозволяють уможливити неспростовність. У разі вирішення питання про використання цифрових підписів чи інших засобів забезпечення цілісності, треба брати до уваги:

– відповідні державні закони та норми;

– відповідну інфраструктуру відкритих ключів;

– вимоги до керування ключами та труднощі, які потрібно подолати для гарантування того, що справжнього поліпшення безпеки досягають без створення нових вразливостей.

3. Неспростовність

Методи криптографії (наприклад, засновані на використанні цифрових підписів) можуть бути використанні для повідомлень, комунікацій та транзакцій з метою підтвердження чи спростування відправлення, передавання, подання, доставлення, оповіщення про отримання тощо.

4. Автентичність даних

У ситуаціях, коли є важливою автентичність даних, для підтвердження достовірності даних може бути використаний цифровий підпис. Ця необхідність проявляється особливо, коли використовуються дані, на які посилає третя сторона, або коли велика кількість людей залежить від точності даних джерел, на які посилаються. Цифрові підписи також можна використовувати для підтвердження факту, що дані створені чи передані певною особою.

5. Керування ключами

Керування ключами охоплює технічні, організаційні та процедурні аспекти, необхідні для використання будь-якого механізму криптографії. Метою керування ключами є безпечне адміністрування та керування криптографічними ключами та пов’язаною з ними інформацією. Керування ключами охоплює генерування, реєстрування, сертифікування, дереєстрування, поширення, встановлення, зберігання, архівування, відгук, виведення та знищення ключового матеріалу. На додаток, важливо розробляти систему керування ключами так, щоб зменшити ризик компрометування ключа та використання ключа неуповноваженими особами. Процедури керування ключами залежать від використовування алгоритму наміру щодо використання ключів та політики безпеки.

Date: 2015-06-11; view: 637; Нарушение авторских прав