Введение. Большая часть задач в химии и химической технологии формулируются как экстремальные: определение оптимальных условий ведения процесса

Большая часть задач в химии и химической технологии формулируются как экстремальные: определение оптимальных условий ведения процесса, оптимального состава реакционной смеси и т.д. В качестве критерия оптимальности могут быть использованы экономические и технологические показатели: прибыль, себестоимость, производительность и т.п.

Корректная постановка задачи оптимизации требует единственности критерия оптимальности и наличия ресурсов оптимизации, т.е. параметров, варьируемых в определенном диапазоне.

Для решения задачи оптимизации применимы два принципиально различных подхода: определение оптимальных условий непосредственно на объекте путем экспериментирования и - определение оптимальных условий функционирования объекта с использованием его математической модели.

Экспериментальная оптимизация применяется в случае, если отсутствует математическая модель объекта, но есть возможность поставить ряд экспериментов на объекте. Область оптимального значения целевой функции достигается путем многократной процедуры экспериментального локального изучения целевой функции и определения оптимальной стратегии продолжения эксперимента. Статистический анализ результатов обеспечивает достоверность.

Второй подход позволяет решать не только задачу оптимизации действующего объекта (задачу анализа), но и задачу оптимального проектирования (задачу синтеза). Широкое использование при этом средств вычислительной техники позволяет экономить время и материальные затраты.

Исходя из вышесказанного, целью выполнения настоящей расчетно-графической работы является освоение стратегии эффективного планирования эксперимента.

1. Постановка задачи экспериментальной оптимизации [1,2]

Если частично или полностью отсутствует информация о механизме процессов, протекающих в реальном объекте (термодинамике, кинетике, гидродинамике), то построение детерминированной математической модели этого объекта для решения задачи его оптимизации не представляется возможным. В таких ситуациях возникает задача экспериментальной оптимизации действующего объекта, т.е. определения оптимальных условий его функционирования путем постановки ряда экспериментов.

Обычно, для эффективного решения задачи, эксперимент заранее планируют.

Общая постановка задачи экспериментальной оптимизации предполагает:

а) выбор критерия оптимальности (целевой функции)

R = f(X), где Х – вектор параметров оптимизации.

Вид зависимости «f» не определен, но есть возможность наблюдать значение целевой функции при заданных значениях параметров оптимизации путем экспериментирования на объекте;

б) выбор параметров оптимизации, т.е. факторов, оказывающих наиболее существенное влияние на целевую функцию и допускающих варьирование в некотором диапазоне. Таким образом, определяются ресурсы оптимизации. Для выбора наиболее существенных факторов на «шумовом поле» можно использовать дисперсионный анализ, метод случайного баланса, метод экспертных оценок;

в) определение значений параметров оптимизации, обеспечивающих экстремум целевой функции R = f(X), определенной в n-мерном пространстве параметров (факторов).

В простейшем случае значения параметров оптимизации варьируются между нижним и верхним значением, т.е. – ограничены:

Х_{i, МIN} ≤ Х_i ≤ Х_{i, МAX} (I = 1,2, ….,n),

а пространство изменения факторов представляет собой гиперкуб. В общем случае факторное пространство имеет более сложный вид.

Параметры оптимизации могут иметь самый различный физический смысл (температура, давление, концентрация и т.д.), поэтому при решении конкретных задач целесообразно оперировать с их безразмерными нормализованными значениями.:

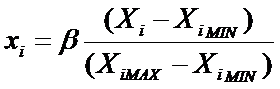
(I = 1,2,,n)

Переменная Х _i при таком способе определения будет изменяться в пределах

0 ≤ Х_i ≤ β, где β – верхняя граница интервала изменения нормализованных параметров.

В настоящей работе предлагается решить задачу экспериментальной оптимизации объекта, условия функционирования которого определяются двумя наиболее существенными факторами (Х₁ и Х₂) при ограничениях

0 ≤ Х_i ≤ 50; (I = 1,2).

Т.е. область определения целевой функции представляет собой квадрат в факторной плоскости, а область изменения – ограниченное 3-х мерное пространство. Решение задачи оптимизации наглядно отображается траекторией движения в плоскости изменения факторов.

Эксперимент на объекте, позволяющий определять значение целевой функции при любых допустимых значениях факторов, в настоящей работе имитируется на ЭВМ. В реализованном алгоритме целевая функция моделируется суммой двух составляющих: детерминированной (зависит от номера варианта задания) и случайной, распределенной по нормальному закону.

Алгоритм позволяет имитировать:

- однократный опыт или серию параллельных опытов в заданной точке пространства оптимизации (изменения факторов);

- полный факторный эксперимент (ПФЭ) в заданной точке пространства оптимизации (изменения факторов);

- ортогональный центральный композиционный план (ОЦКП) в заданной точке пространства оптимизации (изменения факторов).

2. Алгоритм решения задачи экспериментальной оптимизации [3]

Для поиска оптимума целевой функции путем экспериментирования на объекте могут быть использованы методы нелинейного программирования, а также специальные методы экспериментальной оптимизации на объекте в режиме его нормальной эксплуатации. Характерными особенностями экспериментирования в условиях нормальной эксплуатации объекта (установки) являются:

- малые диапазоны варьирования факторов, вследствие ограничений технологического регламента;

- относительно высокий уровень «шума» из-за большого числа неконтролируемых факторов;

- использование менее точной измерительной аппаратуры на промышленных установках по сравнению с лабораторными установками;

- дрейф характеристик объекта.

Специальные методы экспериментальной оптимизации, учитывающие перечисленные особенности, требуют постановки сравнительно небольшого числа опытов при незначительных отклонениях факторов от их номинальных значений.

При выполнении настоящей расчетно-графической работы требуется определить минимальное значение функции двух переменных, заданной неявным способом. Например: зависимости выхода по току (ВТ) от величины плотности тока (i) и рН раствора: BT=f(I,pH).

Для уменьшения времени исследования решено использовать активный эксперимент в виде полного факторного экспери­мента (ПФЭ) или ортогонального центрального композицион­ного плана (ОЦКП). Полученное уравнение регрессии подвер­гается анализу с целью определения направления движения к экстремальной точке. В случае использования ОЦКП этот анализ сводится к использованию либо канонического преоб­разования, либо одного из методов многомерной оптимизации.

Каноническое преобразование заключается в выборе новой системы координат, в которой значительно облегчается геометрический анализ полученного уравнения регрессии. Такого рода преобразования сводятся к определению центра поверхности второго порядка (если он существует), переносу начала координат в новый центр (при этом в уравнении регрессии исчезают линейные члены) и к повороту координатных осей (при этом в уравнении регрессии исчезают парные взаимодействия).

Уравнение регрессии в канонической форме имеет следующий вид:

У – У_s = Q₁₁ * Х ₁² + Q₂₂ * Х ₂² + ….. +Q_КК * Х _К²_,

где У_s – значение функции отклика в новом центре координат (свободный член канонического уравнения);

Х _i – новые оси координат, повернутые в факторном пространстве на некоторый угол относительно старых осей и линейно связанные с ними;

Q_ii – коэффициенты уравнения в канонической форме.

Абсолютные величины и знаки коэффициентов в канонической форме говорят о том, какой вид имеет исследуемая поверхность отклика и где расположен экстремум этой функции.

Процедура канонического преобразования уравнения регрессии состоит из следующих этапов:

а) определение координат центра поверхности второго порядка (Х_1S, X_2S, ……, X_KS) решением системы алгебраических уравнений, получающихся после приравнивания нулю первой производной У по каждому Х:

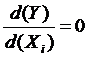
Если при этом определитель полученной системы равен нулю, то поверхность отклика центра не имеет.

Б) определение значения функции отклика в новом центре (У_s) – получение свободного члена канонического уравнения. Для этого полученные в результате решения системы координаты (Х_iS) подставляют в уравнение регрессии.

В) определение величин канонических коэффициентов Q_ii. С этой целью составляют и решают характеристическое уравнение, корнями которого являются искомые канонические коэффициенты.

Г) запись уравнения регрессии в канонической форме и определение типа поверхности отклика.

Нахождение оптимального значения исследуемой функции осложняется тем, что на нее может быть наложено ограничение. Поэтому на последнем этапе работы может отыскиваться условный экстре­мум функции, например с помощью метода неопределенных множителей Лагранжа.