Лабораторная работа № 2

⇐ ПредыдущаяСтр 5 из 6Следующая ⇒

Симплекс-метод

Цель работы: изучить способ решения задач линейного программирования симплекс-методом.

Теоретические сведения.

Пусть имеем задачу линейного программирования в канонической форме:

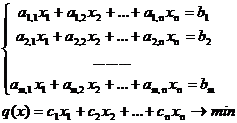
Решение системы называется базисным, если n-m переменных равны нулю. Переменные, которые равны нулю в базисной точке называются небазисными переменными, остальные - базисными.

Симплекс-метод заключается в целенаправленном переборе допустимых базисных решений канонической задачи линейного программирования:

1. Ищется начальная базисная точка.

2. На последующих шагах переход от одного базисного решения к другому осуществляется по правилам.

Правило 1. В базис переводится переменная x_j, которая имеет в целевой функции коэффициент, максимальный по модулю среди отрицательных.

Правило 2. Из базиса исключается переменная x_j, для которой выполняется условие: ,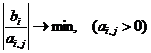

где a_i_,_j – коэффициент при х_j; b_i – свободный коэффициент, правая часть уравнения.

Правило 3. Если целевая функция не содержит отрицательных коэффициентов при х, то оптимальное решение найдено.

Правило 4. Если при с _j не существует a _i _,_j > 0, то задача не имеет решения

Задание. Исходные данные в приложении 2.

1. Привести задачу к каноническому виду.

2. Решить задачу симплекс-методом.

3. Записать результат.

Пример расчета.

Решить задачу симплекс-методом:

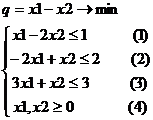
Решение.

1. Приводим задачу к каноническому виду: если знак «≤», то добавляем x_j; если знак «≥», то вычитаем x_j. Если ищется максимум целевой функции, то коэффициенты при x_j умножаем на (-1) и устремляем функцию к минимуму.

У нас получилось 5 переменных: х 1, х 2, х 3, х 4, х 5. Разбиваем переменные на 2 вида: базисные и небазисные. Количество базисных переменных равно числу ограничении, т.е. равно трем. Остальные переменные – небазисные.

2. Составляем начальную симплекс таблицу, т. е. выражаем базисные переменные через небазисные, так чтобы свободные члены в уравнении были неотрицательные.

Выразим переменную x 1 из (1) и подставим в (2) и (3). Тогда из (2) легко найти x 4, из (3) найдем x 5. Подставив х 1 в целевую функцию, получим:

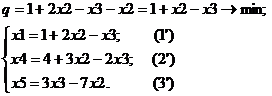
Получили, что х 1, х 4 и х 5 – базисные переменные, а х 2 и х 3 - небазисные. Затем небазисные переменные х 2 и х 3 приравниваем к нулю, подставляем в получившиеся уравнения и находим значения базисных переменных и целевой функции. Таким образом, получили симплекс-таблицу для первой базисной точки:

х 1 х 2 х 3 х 4 х 5 q

Полученная базисная точка соответствует координатам точки С (1;0) (см. стр. 4, рис. 1).

Так как в полученной целевой функции есть отрицательные коэффициент при х 3, то оптимальное решение еще не найдено, поэтому переходим к новому базису.

3. В соответствии с правилом 1 в базис переводим переменную х 3, так как она имеет отрицательный знак в целевой функции. В соответствии с правилом 2:

a ₁₃=1 b ₁=1 b ₁/ a ₁₃=1 - min

a ₄₃=2 b ₄=4 b ₄/ a ₄₃=2

a ₅₃=-3 b ₅=0 a ₅₃< 0

из базиса исключаем х 1 _, т. к. ему соответствует минимальное значение.

Выражаем переменную x 3 из уравнения (1’) и подставляем в остальные уравнения и целевую функцию.

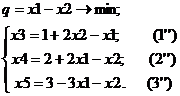
Небазисные переменные х 1 и х 2 приравниваем к нулю, подставляем в получившиеся уравнения и находим значения базисных переменных и целевой функции. Таким образом, получили симплекс-таблицу для второй базисной точки:

х 1 х 2 х 3 х 4 х 5 q

Полученная базисная точка соответствует координатам точки О (0; 0) (см. стр. 4, рис. 1).

Так как в полученной целевой функции есть отрицательные коэффициент при х 2, то оптимальное решение еще не найдено, поэтому переходим к новому базису.

4. В соответствии с правилом 1 в базис переводим переменную х 2, так как она имеет отрицательный знак в целевой функции. В соответствии с правилом 2:

a ₃₂=-2 b ₃=1 a ₃₂< 0

a ₄₂=1 b ₄=2 b ₄/ a ₄₂=2 - min

a ₅₂=1 b ₅=3 b ₅/ a ₅₂=3

из базиса исключаем х 4 _, т. к. ему соответствует минимальное значение.

Выражаем переменную x 2 из уравнения (2’’) и подставляем в остальные уравнения и целевую функцию.

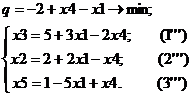
Небазисные переменные х 1 и х 4 приравниваем к нулю, подставляем в получившиеся уравнения и находим значения базисных переменных и целевой функции. Таким образом, получили симплекс-таблицу для третьей базисной точки:

х 1 х 2 х 3 х 4 х 5 q

-2

Полученная базисная точка соответствует координатам точки А (0; 2) (см. стр. 4, рис. 1).

Так как в полученной целевой функции есть отрицательные коэффициент при х 1, то оптимальное решение еще не найдено, поэтому переходим к новому базису.

5. В соответствии с правилом 1 в базис переводим переменную х 1, так как она имеет отрицательный знак в целевой функции. В соответствии с правилом 2:

a₃₁=2 b₃=5 b₃/a₃₁=5/2

a₂₁=1 b₂=2 b₂/a₂₁=2

a₅₁=5 b₅=1 b₅/a₅₁=1/5 - min

из базиса исключаем х 5, т. к. ему соответствует минимальное значение.

Выражаем переменную x 1 из уравнения (3’’’) и подставляем в остальные уравнения и целевую функцию.

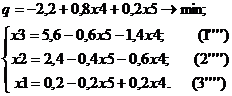
Небазисные переменные х 4 и х 5 приравниваем к нулю, подставляем в получившиеся уравнения и находим значения базисных переменных и целевой функции. Таким образом, получили симплекс-таблицу для четвертой базисной точки:

х 1 х 2 х 3 х 4 х 5 q

0,2 2,4 5,6 -2,2

Полученная базисная точка соответствует координатам точки В (0,2; 2,4) (см. стр. 4, рис. 1).

Так как в полученная целевая функция не содержит отрицательных коэффициентов при х_j, то оптимальное решение найдено.

Ответ: x 1=0,2; x 2=2,4; q =-2,2.

Контрольные вопросы и задания

1.Как записывается каноническая форма задачи линейного программирования?

2. Какие переменные называются базисными?

3. В каком случае решение считается найденным?

4. Всегда ли существует решение задачи линейного программирования? В каком случае у задачи нет решения?

5.Какие значения принимают небазисные переменные в базисной точке?

⇐ Предыдущая 1 2 3 456 Следующая ⇒
Date: 2015-07-17; view: 613; Нарушение авторских прав; Помощь в написании работы --> СЮДА...

mydocx.ru - 2015-2024 year. (0.007 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию