В среде fortran. Студент группы 53224/1 Коленько Г. С

РЕАЛИЗАЦИЯ ЗАДАЧ АППРОКСИМАЦИИ ТАБЛИЧНО ЗАДАННОЙ ФУНКЦИИ, ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА И ПОИСКА ОПТИМУМА

В СРЕДЕ FORTRAN

Выполнил:

студент группы 53224/1 Коленько Г.С.

Проверил:

преподаватель Семеновский В.Б.

СПб

1. АППРОКСИМАЦИЯ ТАБЛИЧНО ЗАДАННОЙ ФУНКЦИИ ПОЛИНОМОМ ВТОРОЙ СТЕПЕНИ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ

Задана функция в табличном виде – набор точек с координатами и 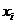. Число точек – n.

Необходимо аппроксимировать параболой эту таблично заданную функцию.

Для нахождения коэффициентов полинома решим следующую систему линейных алгебраических уравнений:

В данной работе решали методом Крамера.

Рис. 1. Исходная функция и аппроксимирующая парабола.

Полученная парабола: .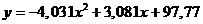

Также для проверки программы в нее были введены точки, принадлежащие параболе . В результате были получены коэффициенты Т.е. программа аппроксимирует корректно.

2. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА МЕТОДОМ ПРЯМОУГОЛЬНИКОВ

В данной работе решали методом средних прямоугольников.

В качестве функции взяли параболу из предыдущего задания.

Формула средних прямоугольников: .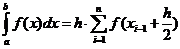

; n – число отрезков, на которые разбивается интервал b-a

Вычисленная сумма для параболы : ;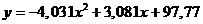

a=-3;b=3.n=100.

Для тестовой параболы на интервале от -3 до +3 при n=50 получили 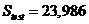, в то время, как аналитически вычисленный интеграл равен 24.

3. ПОИСК ОПТИМУМА ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

В нашем случае оптимум функции – это вершина параболы. Для его нахождения используем метод золотого сечения.

1. Задаем a, b, |b-a|<ε, y=f(x).

2. Из соотношения 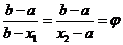находим, что

3. Вычисляем .

4. Если 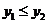(для случая поиска максимума), то 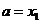, иначе .

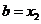5. Если |b-a|<ε, то 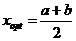, иначе повторяем шаги 2 - 4.

6.

Для тестовой параболы найденный аналитически оптимум .

При точности 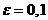программа вычислила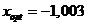

Для полученной параболы :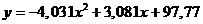

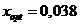
при точности .

4. ТЕКСТ ПРОГРАММЫ

program parabola

integer n, i!Размерность массивов данных, переменная цикла.

real x1(36), y1(36)!Объявление массивов: таблично заданная функция.

real y, xy, x2y, x2, x3, x4, x!Подразумеваются соответствующие суммы.

real det,det1,det2,det3,a,b,c,sum,xopt

write(*,*) 'Enter n'

read*, n

open(1,file='x.txt')!Файл с набором значений аргумента.

read(1,*) x1!(Число точек должно соответствовать n).

open(1,file='y.txt')!Файл с набором значений функции.

read(1,*) y1

y=0.0!Предварительно присваиваем нулевые значения суммам.

xy=0.0

x2y=0.0

x2=0.0

x3=0.0

x4=0.0

x=0.0

do i=1,n!Находим суммы.

y=y+y1(i)

xy=xy+x1(i)*y1(i)

x2y=x2y+x1(i)*x1(i)*y1(i)

x2=x2+x1(i)*x1(i)

x3=x3+x1(i)*x1(i)*x1(i)

x4=x4+x1(i)*x1(i)*x1(i)*x1(i)

x=x+x1(i)

enddo

det=x4*x2*n+x3*x2*x+x3*x2*x-x2*x2*x2-x3*x3*n-x*x*x4!Вычисление определителей.

det1=x2y*x2*n+xy*x2*x+y*x3*x-y*x2*x2-xy*x3*n-x*x*x2y! (Метод Крамера)

det2=x4*xy*n+x2y*x*x2+x3*y*x2-x2*xy*x2-x3*x2y*n-y*x*x4

det3=x4*x2*y+x3*xy*x2+x3*x*x2y-x2*x2*x2y-x3*x3*y-x*xy*x4

a=det1/det!Находим коэффициенты параболы

b=det2/det

c=det3/det

sum=sum1(a,b,c)

xopt=xopt1(a,b,c)

write(*,*)'The equation of the parabola: y=ax^2+bx+c'!Вывод коэффициентов на дисплей.

write(*,*)'a=',a

write(*,*)'b=',b

write(*,*)'c=',c

write(*,*)'sum=',sum

write(*,*)'xopt=',xopt

stop

end

function sum1(a, b, c)!Функция для вычисления интеграла.

integer i, n1

real sum1, a, b, c, h, x, f, s, k, l

write(*,*)'Enter n1'

read*,n1

k=-3.0!Задание границ интервала.

l=3.0

h=(l-k)/n1

x=k+h/2!Метод средних прямоугольников.

s=0.0

do i=1,n1

f=abs(a*x*x+b*x+c)

s=s+f

x=x+h

enddo

sum1=h*s

end function

function xopt1(a,b,c)!Функция для нахождения оптимума функции

real a,b,c,xopt1,x1,y1,x2,y2,e,fi,aa,bb

fi=1.618!Метод золотого сечения

write(*,*)'Enter e'

read*,e

aa=-3.0

bb=3.0

do while (abs(bb-aa) >= e)

x1=bb-(bb-aa)/fi

x2=aa+(bb-aa)/fi

y1=a*x1*x1+b*x1+c

y2=a*x2*x2+b*x2+c

if(y1 <= y2) then

aa=x1

else

bb=x2

endif

enddo

xopt1=(aa+bb)/2

end function

5. РЕЗУЛЬТАТЫ ВЫПОЛНЕНИЯ ПРОГРАММЫ

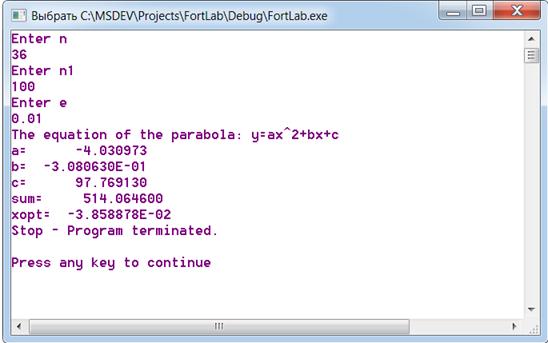
6. СОДЕРЖИМОЕ ФАЙЛОВ С ИСХОДНЫМИ ДАННЫМИ.

xtest.txt: -1.0 0.0 1.0

ytest.txt: 0.0 1.0 4.0

x.txt:

-3.141592654 -2.967059728 -2.792526803 -2.617993878 -2.443460953 -2.268928028 -2.094395102 -1.919862177 -1.745329252 -1.570796327 -1.396263402 -1.221730476 -1.047197551 -0.872664626 -0.698131701 -0.523598776 -0.34906585 -0.174532925 0 0.174532925 0.34906585 0.523598776 0.698131701 0.872664626 1.047197551 1.221730476 1.396263402 1.570796327 1.745329252 1.919862177 2.094395102 2.268928028 2.443460953 2.617993878 2.792526803 2.967059728

y.txt:

73.061 72.5705 73.061 71.5895 70.6085 72.5705 72.08 71.099 71.0009 71.099 78.947 85.3235 90.719 100.0385 105.7283 106.415 106.3169 106.3169 106.3169 106.415 106.415 106.415 106.3169 103.9625 95.624 89.2475 79.4375 70.6085 70.118 70.6085 72.08 72.5705 72.08 71.099 72.08 72.5705

Date: 2015-07-17; view: 437; Нарушение авторских прав