Метод Гира

В начале получаем одним из методов Рунге-Кутты решение y₁, y₂, y₃ задачи Коши

y′ = f(x, y), y(x₀) = y₀ (1)

в точках x₁, x₂, x₃. В окрестности узлов x₀, …, x₄ искомое решение y(x) приближенно заменим интерполяционным полиномом Ньютона четвёртой степени:

y(x)=y₀+y₀₁(x-x₀)+y₀₁₂(x-x₀)(x-x₁)+y₀₁₂₃(x-x₀)(x-x₁)(x-x₂)+y₀₁₂₃₄(x-x₀)(x-x₁)(x-x₂)(x-x₃) (2)

где y₀₁, …, y₀₁₂₃₄ – разделённый разности первого – четвёртого порядков.

Левую часть (1) приближенно найдём путем дифференцирования по х полинома (2)

y′(x)=y₀₁+y₀₁₂(x-x₀+ x-x₁)+y₀₁₂₃[(x-x₀)(x-x₁)+(x-x₀)(x-x₂)+(x-x₁)(x-x₂)]+ y₀₁₂₃₄[(x-x₀)(x-x₁)(x-x₂)+ (x-x₀)(x-x₁)(x-x₃)+ (x-x₀)(x-x₂)(x-x₃)+ (x-x₁)(x-x₂)(x-x₃)] (3)

Разделённые разности для узлов выражаются через узловые значения аппроксимируемой функции

y₀₁ = (y₁-y₀) / h,

y₀₁₂ = (y₂-2y₁+ y₀) / (2h²), (4)

y₀₁₂₃ = (y₃-3y₂+3y₁- y₀) / (2h³),

y₀₁₂₃₄ = (y₄-4y₃+6y₂-4y₁+ y₀) / (24h⁴),

где h = x_j+1 - x_{j .}

Полагая в выражении для производной (3) значение аргумента x = x₄ и учитывая значения разделённых разностей (4), получим:

y′(x₄) = (3y₀ - 16 y₁ + 36 y₂ – 48y₃ + 25y₁) / (12h) (5)

C другой стороны, уравнение (1) при x = x₄ принимает вид:

y′(x₄) = f(x₄,y₄). (6)

Приравниваем правые части соотношений (5) и (6) и найдём:

y₄ = [ 3(4hf(x₄,y₄) - y_o) +16y₁-36y₂+48y₃] / 25 (7)

Формула (7) представляет собой неявную схему Гира четвертого порядка для решения задачи Коши. Изменяя количество x_j, можно аналогичным способом получить формулы Гира как более низких, так и более высоких порядков.

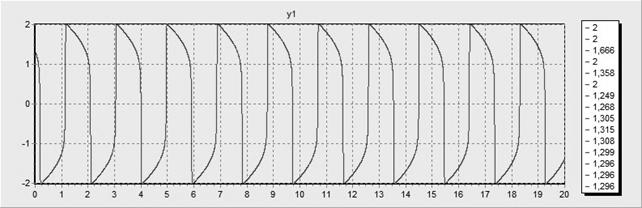
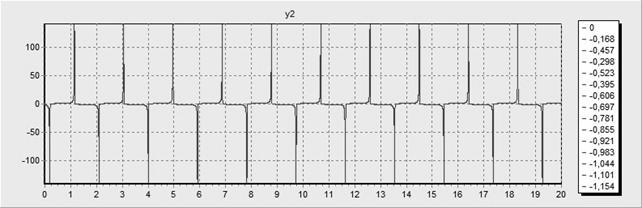
С помощью формулы Гира решим уравнение Ван-дер-Поля. Его можно записать в виде системы:

,

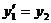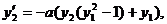
В расчётах рассматриваем 2 случая: a=10 и a=100. Для тестов обычно полагают y₁=2, y₂=0. Конечное время интегрирования системы положить T_k=20.

Код программы:

vector=array[1..2]of double;

var

Form1: TForm1;

a,b,t,Tk:double;

mas1,mas2,mas3:array[0..3]of double;

function f1(y1,y2:double):double;

function f2(y1,y2,a:double):double;

procedure Runge_Kutta(x0,y0,h:double);

procedure Gir(y10,y20,h,e:double);

implementation

{$R *.dfm}

procedure TForm1.Button1Click(Sender: TObject);

var y10,y20,h,e:double;

begin

Form1.Series1.Clear;

Form1.Series4.Clear;

If RadioGroup1.ItemIndex=0 then a:=10 else a:=100;

y10:=StrToFloat(edit1.Text);

y20:=StrToFloat(Edit2.Text);

h:=StrToFloat(edit4.Text);

e:=StrToFloat(edit5.Text);

Gir(y10,y20,h,e);

end;

function f1(y1,y2:double):double;

begin

result:=y2;

end;

function f2(y1,y2,a:double):double;

begin

result:=-a*(y2*(y1*y1-1)+y1);

end;

procedure Runge_Kutta(x0,y0,h:double);

var k1,k2,k3,k4,xn,yn,zn,xn1,yn1,zn1:double;

i:byte;

begin

xn1:=x0;

yn1:=y0;

t:=0;

Form1.Series1.addxy(t,(x0));

Form1.Series4.addxy(t,(0));

mas1[0]:=x0;

mas2[0]:=y0;

for i:=1 to 3 do

begin

t:=t+h;

xn:=xn1; //y1

yn:=yn1; //y2

k1:=f1(xn,yn)*h;

k2:=f1(xn+0.5*k1,yn+0.5*k1)*h;

k3:=f1(xn+0.5*k2,yn+0.5*k2)*h;

k4:=f1(xn+k3,yn+k3)*h;

xn1:=xn+(k1+2*k2+2*k3+k4)/6;

k1:=f2(xn,yn,a)*h;

k2:=f2(xn+0.5*k1,yn+0.5*k1,a)*h;

k3:=f2(xn+0.5*k2,yn+0.5*k2,a)*h;

k4:=f2(xn+k3,yn+k3,a)*h;

yn1:=yn+(k1+2*k2+2*k3+k4)/6;

Form1.series1.addxy(t,(xn1));

Form1.series4.addxy(t,(yn1));

mas1[i]:=xn1;

mas2[i]:=yn1;

end;

end;

function Iteracii(var x0,y0,e:double):vector;

var Xi,Xi1,Yi,Yi1:double;

n:integer;

h:double;

begin

n:=0;

h:=strtofloat(Form1.edit4.Text);

xi1:=x0;

yi1:=y0;

repeat

begin

xi:=xi1;

yi:=yi1;

n:=n+1;

xi1:=(3*(4*h*f1(xi,yi)-mas1[0])+16*mas1[1]-36*mas1[2]+48*mas1[3])/25;

yi1:=(3*(4*h*f2(xi1,yi,a)-mas2[0])+16*mas2[1]-36*mas2[2]+48*mas2[3])/25;

end

until (((abs(xi1-xi))<e) and ((abs(yi1-yi))<e));

result[1]:=xi1;

result[2]:=yi1;

end;

procedure Gir(y10,y20,h,e:double);

var nextyy:vector;

t:double;

begin

Runge_Kutta(y10,y20,h);

t:=0;

nextyy[1]:=4*h*f1(mas1[3],mas2[3])+(1-10*mas1[3])/3-2*mas1[1]+6*mas1[2];

nextyy[2]:=4*h*f2(mas1[3],mas2[3],a)+(0-10*mas2[3])/3-2*mas2[1]+6*mas2[2];

while t<=20 do

begin

t:=t+h;

Form1.series1.addxy(t,(nextyy[1]));

Form1.series4.addxy(t,(nextyy[2]));

mas1[0]:=mas1[1]; mas2[0]:=mas2[1];

mas1[1]:=mas1[2]; mas2[1]:=mas2[2];

mas1[2]:=mas1[3]; mas2[2]:=mas2[3];

mas1[3]:=nextyy[1]; mas2[3]:=nextyy[2];

nextyy:=Iteracii(mas1[3],mas2[3],e);

end;

end;

procedure TForm1.RadioGroup1Click(Sender: TObject);

begin

Button1.Visible:=true;

end;

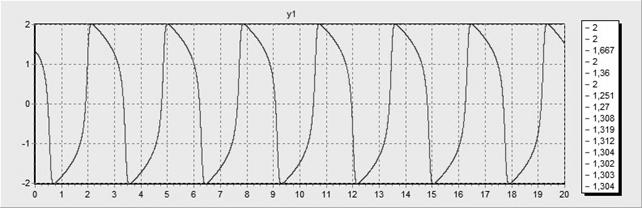
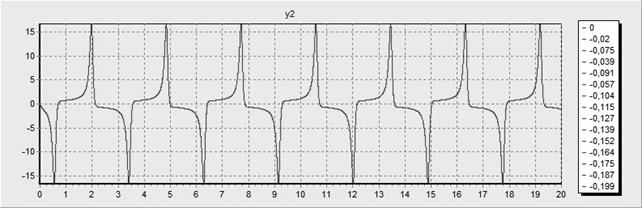
При шага равном 0,001 и точности равной 0,001 мы получаем следующие графики:

· При параметре a =10:

· При параметре a =100:

Список используемой литературы

1. Райзер Ю.П. «Физика газового разряда» издание второе 1992г.

2. Зельдович Я.В. Райзер Ю.П. «Физика ударных волн и высокотемпературных гидродинамических явлений» 1966г.

3. Мудров А.Е. «Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль» 1991г.