Моделирование системы управления
Моделирование системы управления осуществляется с целью исследования следующих свойств системы:
· инвариантность к возмущениям
· ковариантность с заданием
· устойчивость
Для моделирования необходимо записать полную модель системы в единообразной форме. Для этого преобразуем уравнение работы регулятора в дифференциальную форму, включая уравнения модели объекта и уравнения модели регуляторов.
 = KP1 = KP1 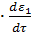 + + 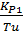 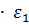 ; ;  1 = 1 = 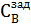 - у1; у1= СВ - у1; у1= СВ
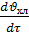 = KP2 = KP2 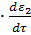 + + 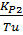 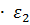 ; ;  2 = tзад – у4; у4= t 2 = tзад – у4; у4= t
Программа моделирования системы управления в среде Mathcad
Таблица соответствия переменных
Таблица 4
| теплоемкость вещества в аппарате и входных потоках,кДж/(кг*К)
| | теплоемкость хладоагента, кДж/(кг*К)
| | плотность вещества в аппарате и входных потоках, кг/л
| | плотность хладоагента, кг/л
| | коэффициент теплопередачи, кДж/(м^2*мин*К)
| | поверхность теплообмена, м^2
| | тепловой эффект рекции, кДж/моль
| | предэкспоненциальный множитель константы скорости, 1/мин
| | энергия активации, Дж/моль
| | концентрация компонента А на входе, моль/л
| | расход первого потока на входе в реактор, л/мин
| | расход второго потока на входе в реактор, л/мин
| | расход на выходе из реактора, л/мин
| | расход хладоагента, л/мин
| | температура первого потока на входе в реактор, С
| | температура второго потока на входе в реактор, С
| | температура хладоагента на входе, С
|
| Вектор-функция правых частей диф.уравнений модели
| | промежуток времени от 0 до N
|
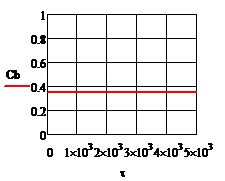
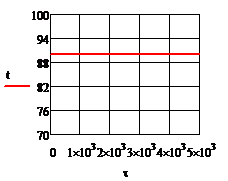
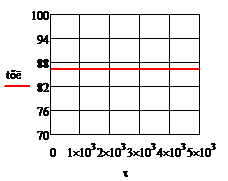
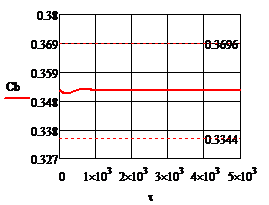
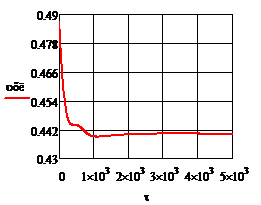
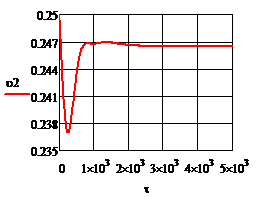
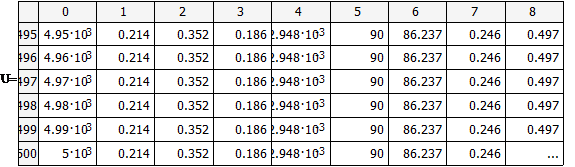 При отсутствии возмущения на объект и при условии задания в качестве исходных данных значений переменных в статике процесс регулирования представляет собой прямые линии параллельные оси времени. На рис.4.1.1. представлены графики изменения выходных переменных и упрощающих воздействий для изложенных условий. При отсутствии возмущения на объект и при условии задания в качестве исходных данных значений переменных в статике процесс регулирования представляет собой прямые линии параллельные оси времени. На рис.4.1.1. представлены графики изменения выходных переменных и упрощающих воздействий для изложенных условий.
Рис.4.1.1.Процесс регулирования при отсутствии возмущений
а) 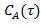 ; б) ; б)  ; в) ; в) 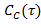 ; г) ; г) 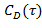 ; д) ; д)  ; е) ; е) 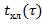 ; ж) ; ж)  ; з) ; з)  . .
Для уточнения параметров подадим возмущение по 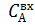 . Процент отклонения 25%. . Процент отклонения 25%. 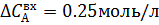 . .
Исходя из требований к безопасности ведения технологического процесса и требований к качеству продукции величины допустимых значений статической ошибки, динамической ошибки и времени регулирования принимаются следующими:
∆( =0.352 =0.352
 = ∆( = ∆(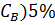 =0.0176 =0.0176
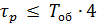
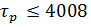
| ∆( =90 =90
 = ∆( = ∆(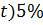 =4.5 =4.5
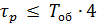
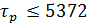
|
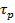 = 360 мин = 360 мин
 = 0.01818 = 0.01818
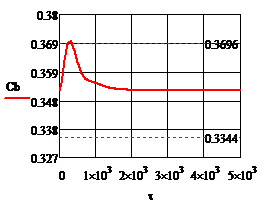 ∆=0 ∆=0
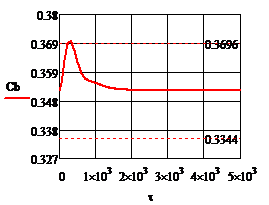
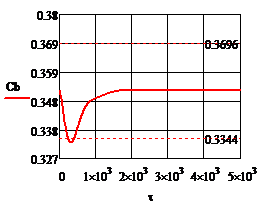
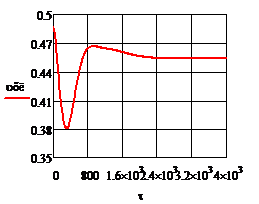
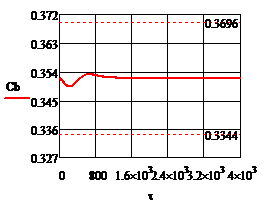
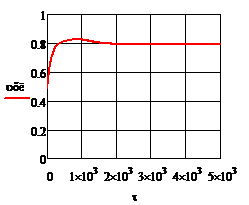
Рис.4.1.2. Процесс регулирования концентрации при возмущении 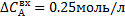
 = 0мин = 0мин
 = 1.844 = 1.844
 ∆=0 ∆=0
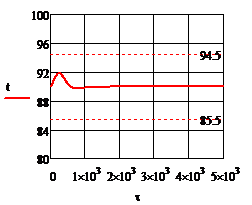
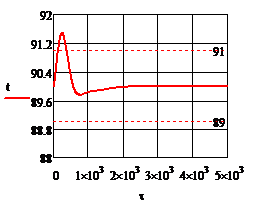
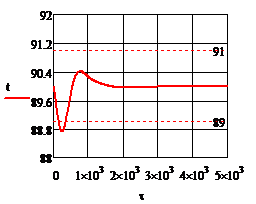
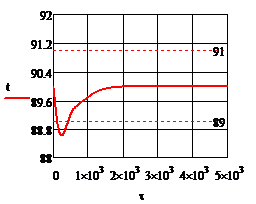
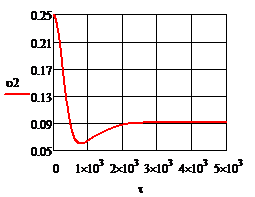
Рис.4.1.3. Процесс регулирования температуры при возмущении 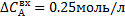
Можно сделать вывод, что настройки регулятора удовлетворены. Следовательно, значения параметров алгоритмов регулирования следующие:
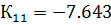
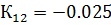
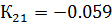
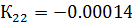
Инвариантность к возмущениям
Инвариантность к возмущениям означает способность системы компенсировать возмущения при заданной величине задания по каждому контуру.
1) ∆ 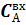 = = 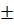 0,25 моль/л, Процент отклонения 25% 0,25 моль/л, Процент отклонения 25%
∆( =0.352 =0.352
 = ∆( = ∆(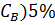 =0.0176 =0.0176
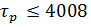
| ∆( =90 =90
 = ∆( = ∆(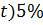 =4.5 =4.5
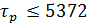
|
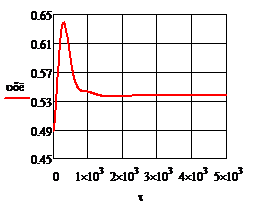
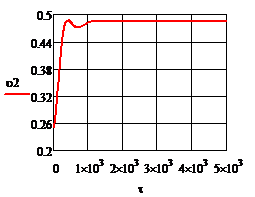
Рис.4.2.1. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при ∆ 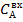 = 0,25 моль/л = 0,25 моль/л
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  . .
Рис. 4.2.2. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при ∆ 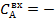 0,25 моль/л 0,25 моль/л
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  . .
Анализ результатов моделирования представленных на рис. 4.2.1. и рис.4.2.2. показывает:
· Величина статической и динамической ошибки лежат в переделах допустимых значений;
· Время регулирования также удовлетворяет сформулированным требованиям;
· Значение расхода  , при отрицательной подаче возмущения, оказалось отрицательным, что не имеет физического смысла и не может быть реализовано. , при отрицательной подаче возмущения, оказалось отрицательным, что не имеет физического смысла и не может быть реализовано.
Следовательно, необходимо проанализировать работу системы при меньших возмущениях или наложить ограничения на регулирующие воздействия: если 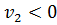 , то принять , то принять 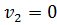 . .
Подадим возмущение по 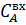 с процентом отклонения 20%. с процентом отклонения 20%.
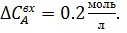  = 1 = 1
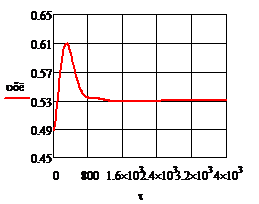
Рис.4.2.3. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при ∆ 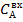 = 0,2 моль/л = 0,2 моль/л
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  . .
∆( =0 =0
 = 0.01402 = 0.01402
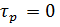
| ∆( =0 =0
 = 1.42 = 1.42
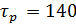
|
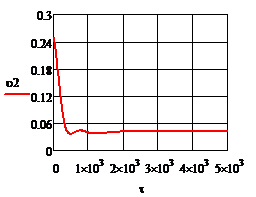
Рис. 4.2.4. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при ∆ 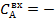 0,2 моль/л 0,2 моль/л
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  . .
∆( =0 =0
 = 0.01507 = 0.01507
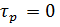
| ∆( =0 =0
 = 1.282 = 1.282
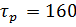
| Анализ результатов моделирования представленных на рис. 4.2.3. - рис.4.2.4. показывают:
· Величина статической и динамической ошибки лежат в переделах допустимых значений;
· Время регулирования также удовлетворяет сформулированным требованиям;
· Значения расходов  и и 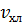 при подаче возмущений имеют физический смысл. при подаче возмущений имеют физический смысл.
2) ∆t1= 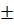 10 10  , Процент отклонения 33% , Процент отклонения 33%
∆( =0.352 =0.352
 = ∆( = ∆(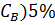 =0.0176 =0.0176
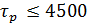
| ∆( =90 =90
 = ∆( = ∆(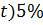 =4.5 =4.5
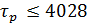
|
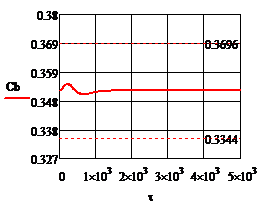
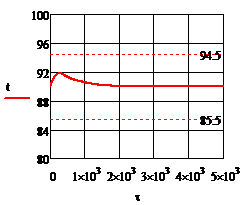
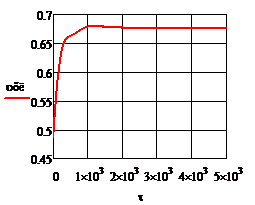
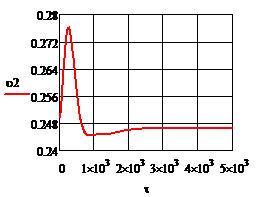
Рис.4.2.5. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при ∆t1=10 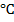
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  . .
∆( =0 =0
 = 0.00237 = 0.00237
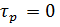
| ∆( =0 =0
 = 1.838 = 1.838
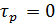
|
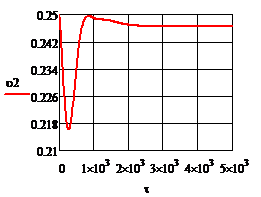
Рис.4.2.6. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при ∆t1= - 10 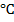
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  . .
∆( =0 =0
 = 0.00296 = 0.00296
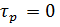
| ∆( =0 =0
 = 1.695 = 1.695
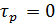
|
3) ∆t2= 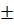 10 10  , Процент отклонения 25% , Процент отклонения 25%
∆( =0.352 =0.352
 = ∆( = ∆(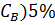 =0.0176 =0.0176
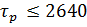
| ∆( =90 =90
 = ∆( = ∆(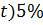 =4.5 =4.5
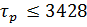
|
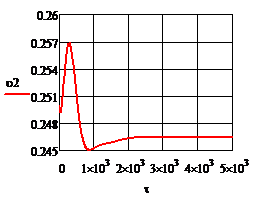
Рис. 4.2.7. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при ∆t2= 10 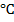
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  . .
∆( =0 =0
 = 0.00062 = 0.00062
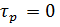
| ∆( =0 =0
 = 0.69 = 0.69
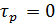
|
Рис. 4.2.8. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при ∆t2= - 10 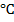
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  . .
∆( =0 =0
 = 0.00115 = 0.00115
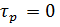
| ∆( =0 =0
 = 0.482 = 0.482
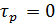
|
4) ∆ 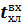 = = 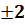 0 0  , Процент отклонения 67% , Процент отклонения 67%
∆( =0.352 =0.352
 = ∆( = ∆(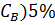 =0.0176 =0.0176
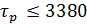
| ∆( =90 =90
 = 1 = 1
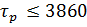
|
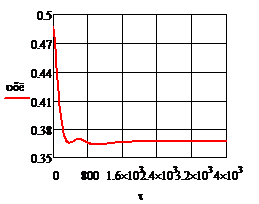
Рис. 4.2.9. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при ∆ 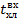 = 20 = 20 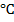
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  . .
∆( =0 =0
 = 0.0025 = 0.0025
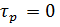
| ∆( =0 =0
 = 2.24 = 2.24
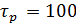
|
Рис. 4.2.10. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при ∆ 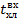 = - 20 = - 20 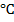
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  . .
∆( =0 =0
 = 0.00245 = 0.00245
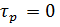
| ∆( =0 =0
 = 1.391 = 1.391
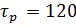
|
5) ∆ 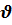 1 = 1 = 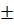 0,2 л/мин, Процент отклонения 27% 0,2 л/мин, Процент отклонения 27%
∆( =0.352 =0.352
 = ∆( = ∆(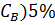 =0.0176 =0.0176
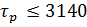
| ∆( =90 =90
 = ∆( = ∆(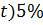 =4.5 =4.5
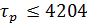
|
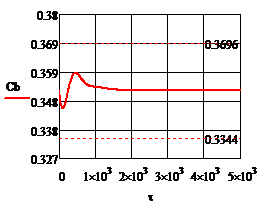
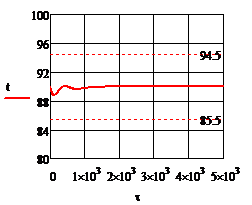
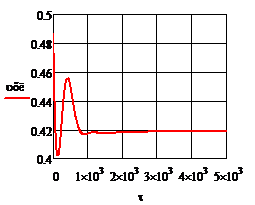
Рис. 4.2.11. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при ∆  1 = 0,2 л/мин 1 = 0,2 л/мин
а) 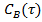 ; б) ; б)  ; в) ; в) 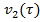 ; г) ; г) 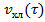 . .
∆( =0 =0
 = 0.00655 = 0.00655
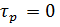
| ∆( =0 =0
 = 1.172 = 1.172
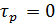
|
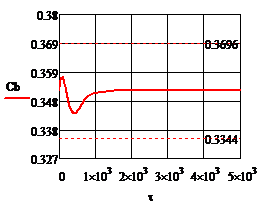
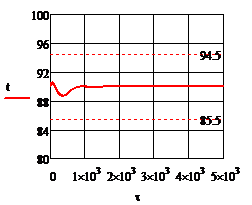
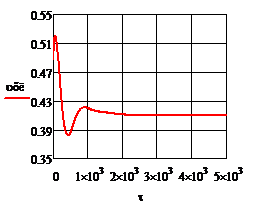
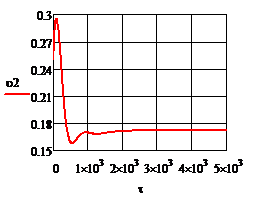
Рис. 4.2.12. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при ∆  1 = - 0,2 л/мин 1 = - 0,2 л/мин
а) 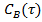 ; б) ; б)  ; в) ; в) 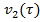 ; г) ; г) 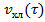 . .
∆( =0 =0
 = 0.00478 = 0.00478
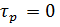
| ∆( =0 =0
 = 0.52 = 0.52
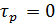
| Анализ результатов моделирования представленных на рис. 4.2.5. и рис.4.2.12. показывает:
· Величина статической и динамической ошибки лежат в переделах допустимых значений;
· Время регулирования также удовлетворяет сформулированным требованиям;
· Значения расходов  и и 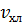 при подаче возмущений имеют физический смысл. при подаче возмущений имеют физический смысл.
Ковариантность с заданием
Ковариантность с заданным возмущением означает способность системы отслеживать изменение задания в отсутствие других возмущений.
Моль/л
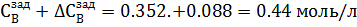
Рис.4.3.1. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при 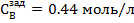
а) 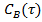 ; б) ; б)  ; в) ; в) 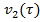 ; г) ; г) 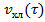 . .
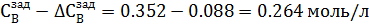
Рис.4.3.2. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при 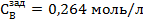
а) 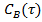 ; б) ; б)  ; в) ; в) 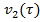 ; г) ; г) 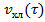 . .
2. ∆tзад = 20% = 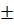 18 18 
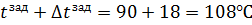
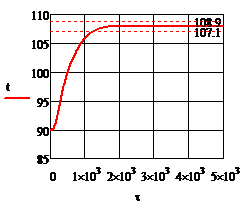
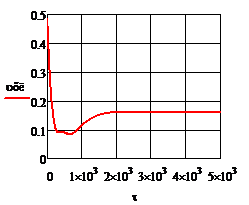
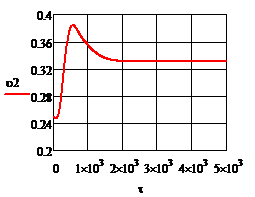
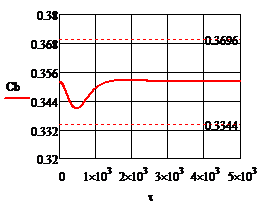
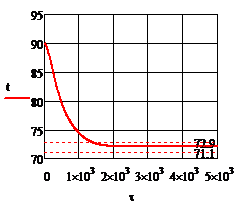
Рис.4.3.3. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при 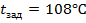
а) 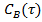 ; б) ; б)  ; в) ; в) 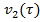 ; г) ; г) 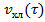 . .
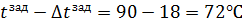
Рис.4.3.4. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при 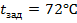
а) 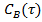 ; б) ; б)  ; в) ; в) 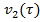 ; г) ; г) 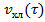 . .
3. ∆tзад = 20% = 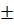 18 18  , ∆ , ∆ 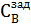 = 25% = = 25% = 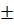 0,088 моль/л 0,088 моль/л
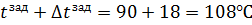
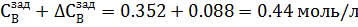
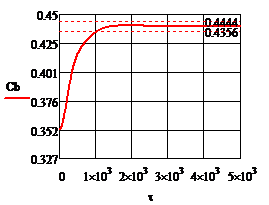
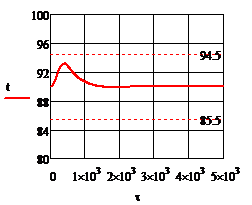
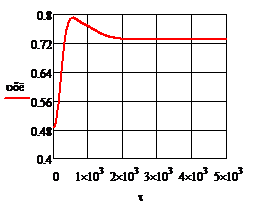
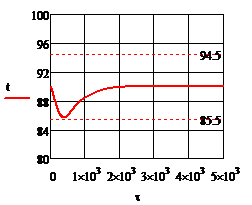
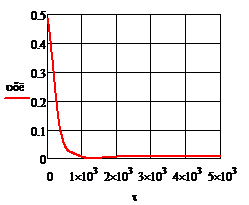
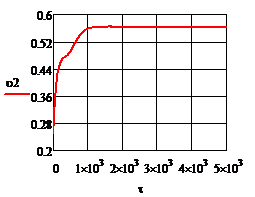
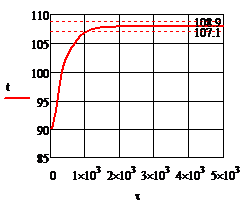
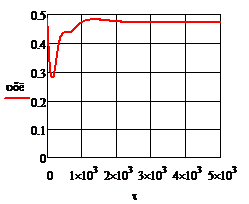
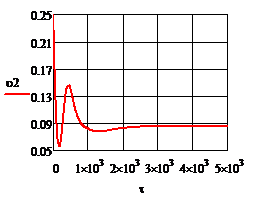
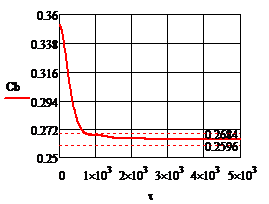
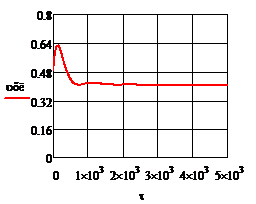
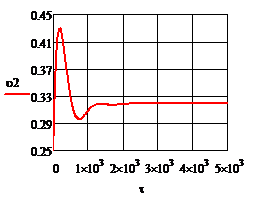
Рис.4.3.5. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при 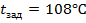 , , 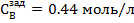
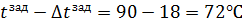
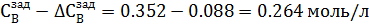
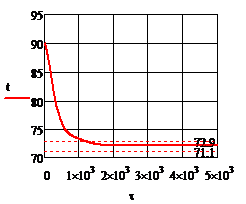
Рис.4.3.5. Изменение регулируемых переменных (Св, t) и регулирующих воздействий
при 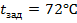 , , 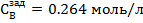
Таблица 5
| канал
| положительное отклонение
| отрицательное отклонение
| 
| 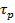
| ∆
| 
| 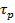
| ∆
| | инвариантность
| 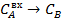
| 0.01402
|
|
| 0.01507
|
|
| 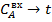
| 1.42
|
|
| 1.282
|
|
| 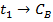
| 0.00237
|
|
| 0.00296
|
|
| 
| 1.838
|
|
| 1.695
|
|
| 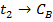
| 0.00062
|
|
| 0.00115
|
|
| 
| 0.69
|
|
| 0.482
|
|
| 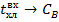
| 0.0025
|
|
| 0.00245
|
|
| 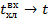
| 2.24
|
|
| 1.391
|
|
| 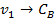
| 0.00655
|
|
| 0.00478
|
|
| 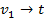
| 1.172
|
|
| 0.52
|
|
| | ковариантность
| 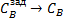
| 0.088
|
|
| 0.088
|
|
| 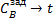
| 3.059
|
|
| 4.289
|
|
| 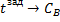
| 0.00944
|
|
| 0.01113
|
|
| 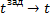
|
|
|
|
|
|
| 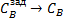
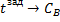
| 0.088
|
|
| 0.088
|
|
| 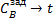
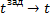
|
|
|
|
|
|
|
По результатам исследования инвариантности и ковариантности можно сделать следующие выводы:
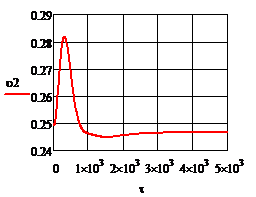
· система устойчива, так как переходные процессы управления затухают при 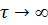 ; ;
· система инвариантна к возмущениям с отклонением в 20-33% и ковариантна с заданием с отклонением 20-25%.
Многомерная система несвязанного управления нелинейным объектом при использовании линейных ПИ алгоритмов работы регуляторов работоспособна.
Date: 2015-07-17; view: 496; Нарушение авторских прав | Понравилась страница? Лайкни для друзей: |
|
|



 = KP1
= KP1 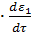 +
+ 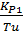
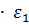 ;
;  1 =
1 = 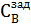 - у1; у1= СВ
- у1; у1= СВ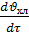 = KP2
= KP2 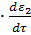 +
+ 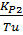
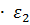 ;
;  2 = tзад – у4; у4= t
2 = tзад – у4; у4= t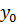

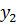

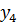

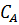
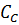
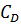
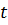
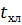

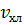
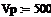
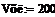
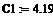
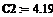


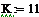
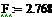
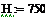


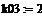
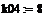
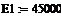
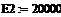
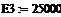
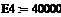
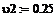
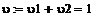
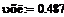
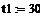

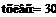
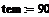
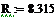
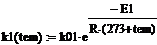
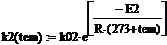

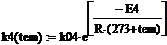
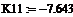

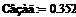

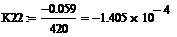
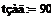
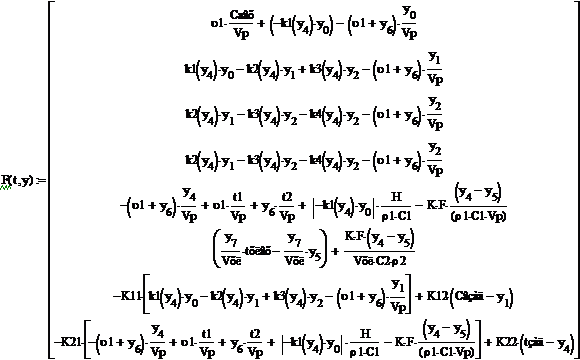
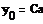
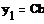
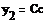
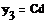
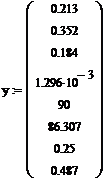
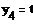
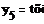
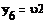

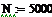
 При отсутствии возмущения на объект и при условии задания в качестве исходных данных значений переменных в статике процесс регулирования представляет собой прямые линии параллельные оси времени. На рис.4.1.1. представлены графики изменения выходных переменных и упрощающих воздействий для изложенных условий.
При отсутствии возмущения на объект и при условии задания в качестве исходных данных значений переменных в статике процесс регулирования представляет собой прямые линии параллельные оси времени. На рис.4.1.1. представлены графики изменения выходных переменных и упрощающих воздействий для изложенных условий.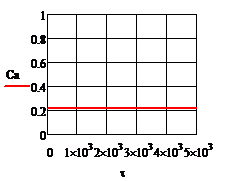
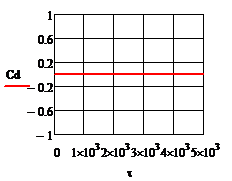
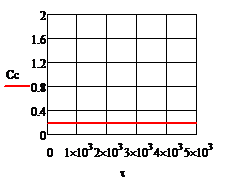
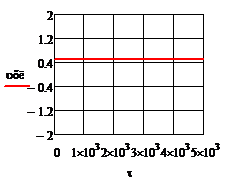
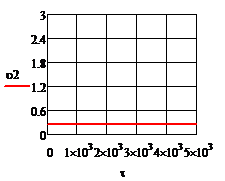
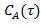 ; б)
; б)  ; в)
; в) 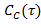 ; г)
; г) 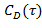 ; д)
; д)  ; е)
; е) 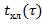 ; ж)
; ж)  ; з)
; з)  .
.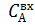 . Процент отклонения 25%.
. Процент отклонения 25%. 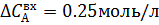 .
. =0.352
=0.352
 = ∆(
= ∆(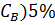 =0.0176
=0.0176
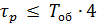
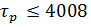
 =90
=90
 = ∆(
= ∆(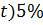 =4.5
=4.5
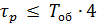
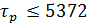
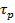 = 360 мин
= 360 мин = 0.01818
= 0.01818 ∆=0
∆=0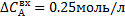
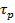 = 0мин
= 0мин = 1.844
= 1.844 ∆=0
∆=0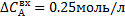
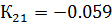
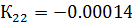
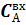 =
= 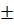 0,25 моль/л, Процент отклонения 25%
0,25 моль/л, Процент отклонения 25% =0.352
=0.352
 = ∆(
= ∆(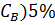 =0.0176
=0.0176
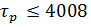
 =90
=90
 = ∆(
= ∆(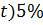 =4.5
=4.5
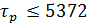
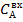 = 0,25 моль/л
= 0,25 моль/л ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.

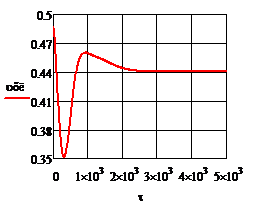

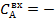 0,25 моль/л
0,25 моль/л ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. , при отрицательной подаче возмущения, оказалось отрицательным, что не имеет физического смысла и не может быть реализовано.
, при отрицательной подаче возмущения, оказалось отрицательным, что не имеет физического смысла и не может быть реализовано.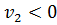 , то принять
, то принять 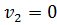 .
.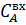 с процентом отклонения 20%.
с процентом отклонения 20%.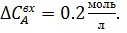
 = 1
= 1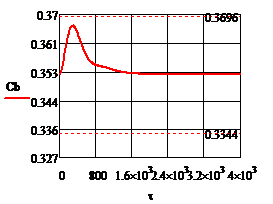

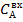 = 0,2 моль/л
= 0,2 моль/л ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. =0
=0
 = 0.01402
= 0.01402
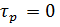
 =0
=0
 = 1.42
= 1.42
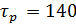

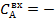 0,2 моль/л
0,2 моль/л ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. =0
=0
 = 0.01507
= 0.01507
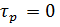
 =0
=0
 = 1.282
= 1.282
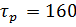
 и
и 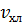 при подаче возмущений имеют физический смысл.
при подаче возмущений имеют физический смысл.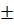 10
10  , Процент отклонения 33%
, Процент отклонения 33% =0.352
=0.352
 = ∆(
= ∆(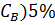 =0.0176
=0.0176
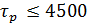
 =90
=90
 = ∆(
= ∆(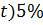 =4.5
=4.5
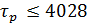
 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. =0
=0
 = 0.00237
= 0.00237
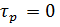
 =0
=0
 = 1.838
= 1.838
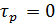
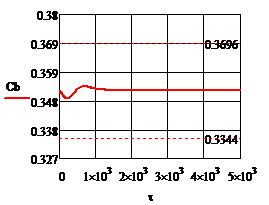
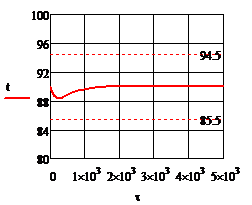
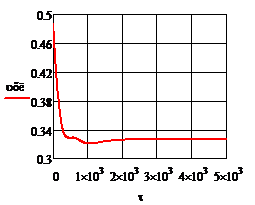
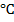
 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. =0
=0
 = 0.00296
= 0.00296
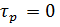
 =0
=0
 = 1.695
= 1.695
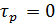
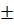 10
10  , Процент отклонения 25%
, Процент отклонения 25% =0.352
=0.352
 = ∆(
= ∆(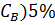 =0.0176
=0.0176
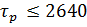
 =90
=90
 = ∆(
= ∆(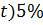 =4.5
=4.5
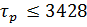
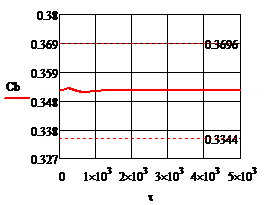
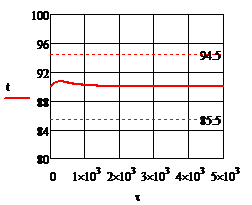
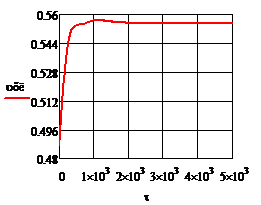
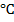
 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. =0
=0
 = 0.00062
= 0.00062
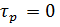
 =0
=0
 = 0.69
= 0.69
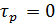

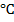
 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. =0
=0
 = 0.00115
= 0.00115
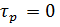
 =0
=0
 = 0.482
= 0.482
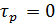
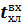 =
= 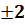 0
0  , Процент отклонения 67%
, Процент отклонения 67% =0.352
=0.352
 = ∆(
= ∆(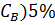 =0.0176
=0.0176
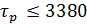
 =90
=90
 = 1
= 1
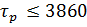



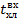 = 20
= 20 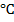
 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. =0
=0
 = 0.0025
= 0.0025
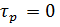
 =0
=0
 = 2.24
= 2.24
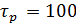

 = - 20
= - 20 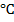
 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. =0
=0
 = 0.00245
= 0.00245
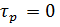
 =0
=0
 = 1.391
= 1.391
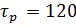
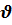 1 =
1 = 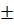 0,2 л/мин, Процент отклонения 27%
0,2 л/мин, Процент отклонения 27% =0.352
=0.352
 = ∆(
= ∆(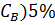 =0.0176
=0.0176
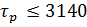
 =90
=90
 = ∆(
= ∆(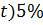 =4.5
=4.5
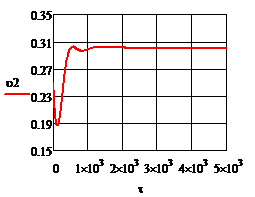
 1 = 0,2 л/мин
1 = 0,2 л/мин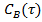 ; б)
; б)  ; в)
; в) 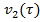 ; г)
; г) 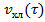 .
. =0
=0
 = 0.00655
= 0.00655
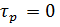
 =0
=0
 = 1.172
= 1.172
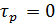
 1 = - 0,2 л/мин
1 = - 0,2 л/мин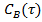 ; б)
; б)  ; в)
; в) 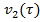 ; г)
; г) 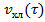 .
. =0
=0
 = 0.00478
= 0.00478
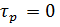
 =0
=0
 = 0.52
= 0.52
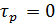
 и
и 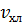 при подаче возмущений имеют физический смысл.
при подаче возмущений имеют физический смысл.

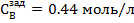
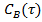 ; б)
; б)  ; в)
; в) 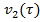 ; г)
; г) 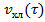 .
.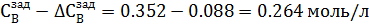

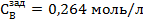
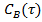 ; б)
; б)  ; в)
; в) 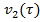 ; г)
; г) 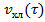 .
.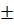 18
18 
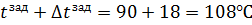

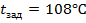
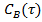 ; б)
; б)  ; в)
; в) 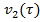 ; г)
; г) 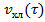 .
.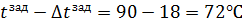
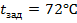
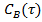 ; б)
; б)  ; в)
; в) 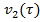 ; г)
; г) 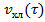 .
.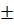 18
18  , ∆
, ∆ 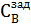 = 25% =
= 25% =  0,088 моль/л
0,088 моль/л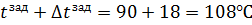
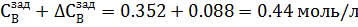

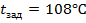 ,
, 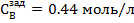
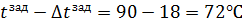
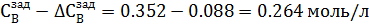
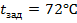 ,
, 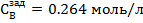

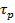

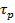
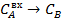
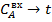
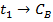

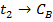

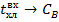
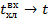
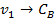
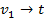
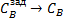
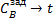
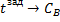
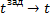
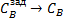
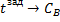
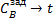
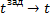
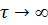 ;
;