Виды и модели анализа технических объектов моделирования

В зависимости от модельного режима, положенного в основу решения конкретной проектной задачи, различают следующие виды анализа:

- статических состояний;

- переходных процессов;

- устойчивости;

- стационарных режимов колебаний;

- частотных характеристик;

- чувствительности;

- статистический.

Анализ статических состояний относится к задачам стати­ки, а остальные виды анализа – к задачам динамики. Исходная математическая модель объекта представляет собой систему нелинейных дифференциальных уравнений, которая в нормальной форме Коши имеет вид:

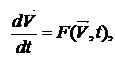
где V – вектор базисных координат; t – независимая перемен­ная (время).

Система уравнений описывает динамические режимы функционирования технического объекта. Анализ этих режимов заключается в решении системы уравнений и последующем определении выходных параметров объекта. Задавая начальные условия V(0)=V₀, находят решения V(t), а затем вычисляют значения выходных параметров Y (целевых функций). Большинство выходных параметров имеют смысл функционалов зависимостей базисных координат. Функционал представляет собой отображение класса функ­ций в класс чисел. Примеры функционалов: определенные интегралы, экстремумы функций, значения функций при заданных значениях аргументов и т. п. Например, коэффициент использования (утилизации) сервера является выходным параметром, значение которого в первую очередь определяется интенсивностью поступления запросов (входная переменная) и интенсивностью их обработки (базисная переменная), а также рядом других факторов – дисциплинами обслуживания, приоритетами запросов и т. д.

Математическая модель рассмотренного вида непосредственно ис­пользуется при анализе переходных процессов, устойчивости, стационарных режимов колебаний. Эта же модель позволяет решать и задачи анализа статических состояний: при dV/dt= 0 система дифференциальных уравнений переходит в систему алгебраических уравнений F(V) =0.

Частотный анализ проводится для определения резонанс­ных режимов, для исследования передачи или преобразования информационных сигналов, представленных в частотной области. Частотными методами можно также решать задачи анализа устойчивости и стационарных режимов колебаний.

Анализ чувствительности выполняется для оценки влияния вариации параметров объекта на изменение выходных функции. Выходные параметры объекта Y непосредственно не фигу­рируют в исходной системе ДУ. Они определяются по результатам решения V(t) системы уравнений.

Статистические методы анализа требуют использования вероятностных моделей. Большинство показателей качества, характеризующие процесс функционирования информационных систем и вычислительных сетей, являются вероятностными (например, вероятность надежного представления информации при выполнении функциональной задачи, вероятность предотвращения несанкционированного доступа и т. п.).

Date: 2015-07-17; view: 493; Нарушение авторских прав