Анализ вариации зависимой переменной. Качество оценивания в модели множественной линейной регрессии

Пусть в уравнении регрессии содержится 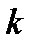объясняющих переменных. Дисперсию зависимой переменной можно представить в виде суммы объясненной и необъясненной составляющих:

,

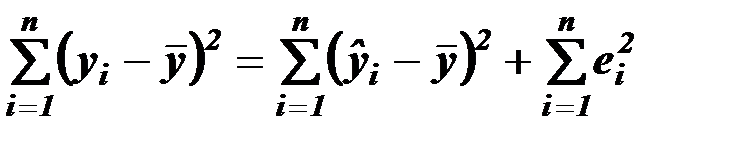где:

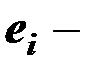остаток в 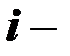м варианте реализации событий;

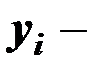значение зависимой переменной в 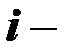м варианте реализации событий;

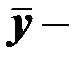среднее значение зависимой переменной;

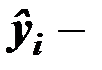расчетное значение зависимой переменной в 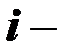м варианте реализации событий, определяемое уравнением регрессии;

число реализации событий, в каждом из которых при сочетании значений независимых переменных было получено значение зависимой переменной.

Каждая сумма в этом разложении имеет собственное название:

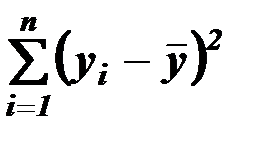― общий разброс зависимой переменной (обозначается );

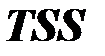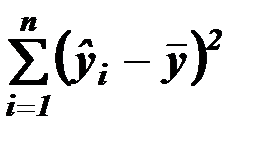― разброс, объясненный регрессией (обозначается );

― разброс, не объясненный регрессией (обозначается ).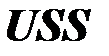

Используя введенные обозначения, разложение дисперсии зависимой переменной можно записать в виде суммы:

.

Мерой объясняющего качества уравнения регрессии по сравнению с оценкой в виде среднего значения 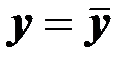является коэффициент детерминации 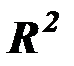, который измеряет долю дисперсии, совместно объясненной всеми независимыми переменными:

.

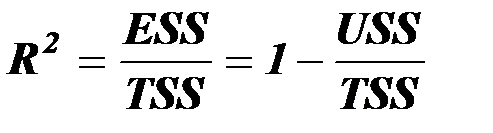В случае коррелированности независимых переменных объясняющие способности этих переменных могут перекрываться. Для компенсации такого увеличения 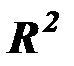вводится приведенный (скорректированный) коэффициент детерминации с поправкой на число независимых переменных, которым можно варьировать (называемое иначе числом степеней свободы):

.

Если при добавлении новой переменной (при этом уменьшается на 1 число степеней свободы) увеличение доли объясненной регрессии мало, то скорректированный коэффициент детерминации 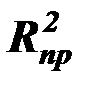может уменьшаться, следовательно, добавлять новую переменную не следует.

Качество оценок для модели множественной линейной регрессии предполагает определение статистической значимости полученных коэффициентов уравнения регрессии и коэффициента детерминации .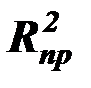

Значимость коэффициентов уравнения регрессии 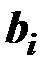оценивается с помощью критерия :

,

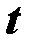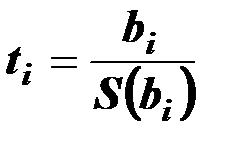где стандартные ошибки коэффициентов регрессии.

Величина 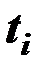имеет распределение Стьюдента с 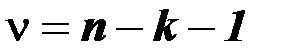степенями свободы, где:

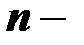число пар данных в выборке, использованных для получения уравнения регрессии;

количество коэффициентов в уравнении регрессии.

Алгоритм оценки значимости для коэффициентов уравнения регрессии состоит в следующем:

1) вычисляется наблюдаемое значение критерия ;

2) по таблице распределения Стьюдента по заданному уровню значимости и числу степеней свободы 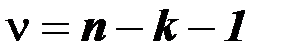находится критическое значение ;

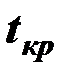3) вычисленные критери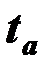и и 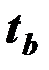сравниваются с критическим значением .

Если 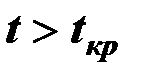, то соответствующий коэффициент уравнения регрессии значим и принимается. Если 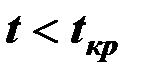, то соответствующий коэффициент уравнения регрессии незначим, не отличается от нуля и не принимается.

В эконометрике проверку гипотез осуществляют при 5%-м, реже на 10%-м уровне значимости. В первом случае стандартная ошибка оценки коэффициента регрессии составляет примерно до половины его величины. Последовательное исключение несущественных факторов (переменных), коэффициенты при которых оказались незначимы, составляют основу пошагового регрессионного анализа.

Для определения статистической значимости коэффициента детерминации 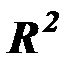используется 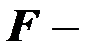статистика:

,

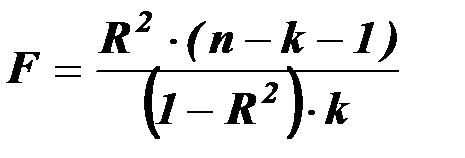где:

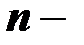число пар данных в выборке, использованных для получения уравнения регрессии;

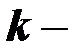количество коэффициентов в уравнении регрессии.

Величина 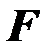имеет распределение Фишера с 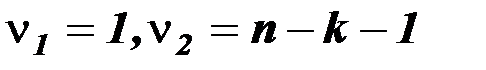степенями свободы. Вычисленный критерий 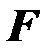сравнивается с критической величиной следующим образом:

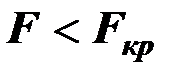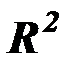если , то считается незначимым, он не отличим от нуля;

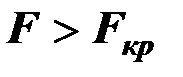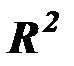если , то считается значимым, и уравнение регрессии может использоваться для объяснения изменения переменной 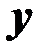под влиянием изменения переменных .

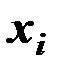Величины критических значений критериев оценки значимости принимаются при 5%-м, реже при 10%-м уровне значимости. Указанные уровни значимости соответствуют 95%-му и 90%-му доверительным интервалам соответственно.

Date: 2015-07-17; view: 684; Нарушение авторских прав