Построение модели множественной линейной регрессии с использованием метода наименьших квадратов (МНК)

В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.

Простая регрессияпредставляет собой модель, где среднее значение зависимой (объясняющей) переменной 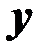рассматривается как функция одной независимой (объясняющей) переменной 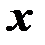, т.е. это модель вида

.

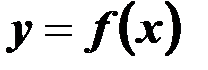Множественная регрессия представляет собой модель, где среднее значение зависимой (объясняющей) переменной 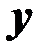рассматривается как функция нескольких независимых (объясняющих) переменных 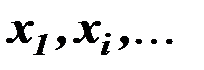, т.е. это модель вида

.

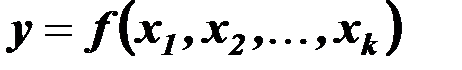Любой эконометрическое исследование начинается со спецификации модели, т.е. с формулировки вида модели исходя из соответствующей теории связи между явлениями.

В первую очередь из всего круга вопросов, влияющих на результативный признак, необходимо выделить наиболее существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.

Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки ― увеличивая объем исходных данных, то ошибки измерения практически могут свести на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при исследовании на макроуровне.

Для построения модели множественной линейной регрессии с 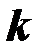объясняющими переменнымизависимость между ними в генеральной совокупности представляется в виде:

,

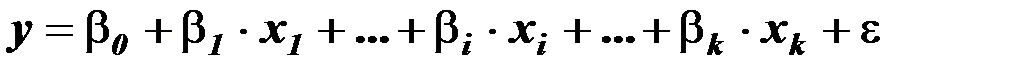где:

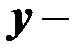объясняемая – зависимая переменная;

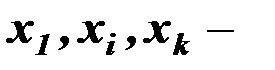объясняющие – независимые переменные;

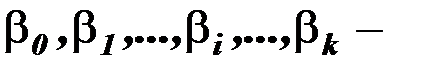параметры модели;

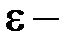случайное слагаемое.

Обычно при построении модели множественной линейной регрессии предполагается отсутствие корреляций всех объясняющих переменных друг с другом.

На основе наблюдений получают выборочное уравнение регрессии:

,

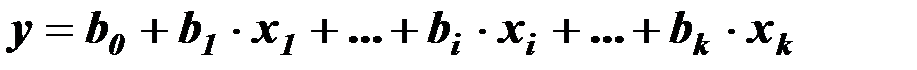где 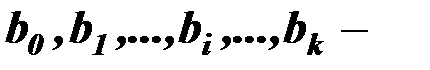оценки параметров .

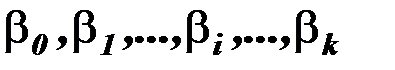Для оценки параметров уравнения регрессии используется метод наименьших квадратов (МНК). Основные идеи МНК рассмотрим на примере частного случая модели множественной линейной регрессии при 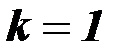(т.е. модели линейной парной регрессии):

.

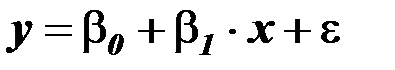При применении МНК неизвестные оценк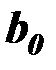и и 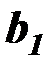параметров уравнения регрессии определяют путем минимизации суммы квадратов остатков:

,

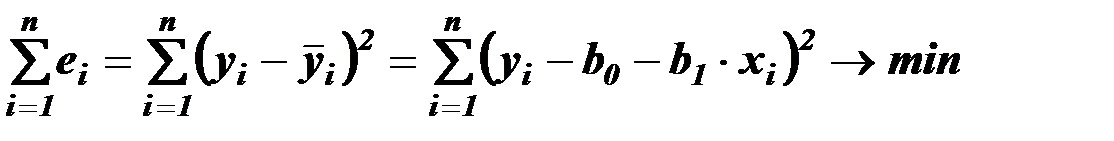где 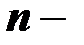количество пар переменных, используемых для анализа.

Необходимое условие минимума обеспечивается приравниванием нулю частных производных суммы квадратов остатков по величинам 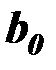и :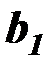

, ,

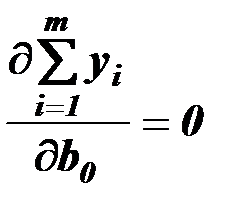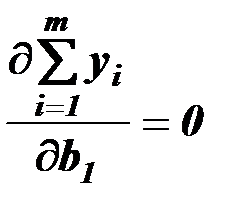где 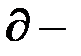значок дифференциала.

Из этих условий вытекают два уравнения для определения величин 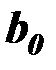и :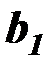

, .

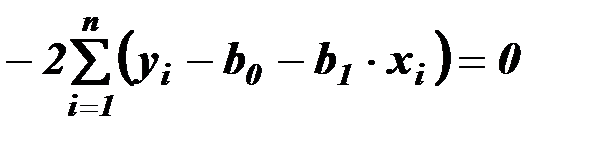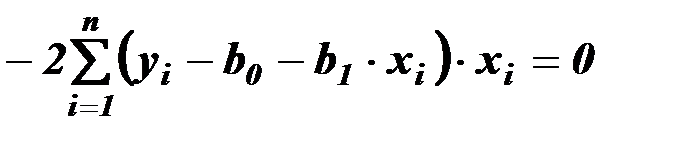Решая систему из двух уравнений, получим:

, ,

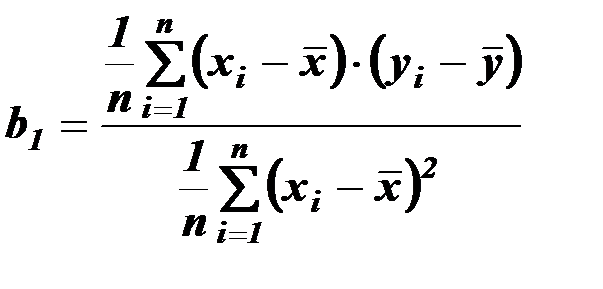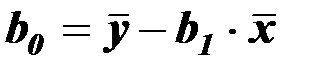где 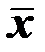и 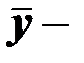выборочные средние значения переменных 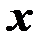и .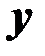

Коэффициент 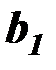, представляющий собой угловой коэффициент регрессии, показывает скорость приращения переменной 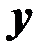при изменении независимой переменной 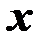и связан с коэффициентом корреляции 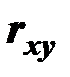величин 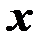и 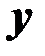соотношением:

,

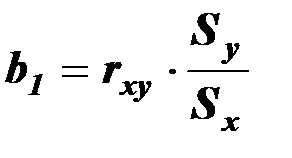где 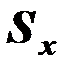и 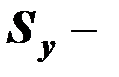среднеквадратические отклонения переменных 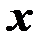и .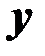

Date: 2015-07-17; view: 570; Нарушение авторских прав