Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Составление уравнений динамики средних
|
|
В ходе боя численности боеспособных единиц сторон будут случайным образом изменяться (уменьшаться, так как пополнение средств поражения сторон мы пока не рассматриваем). Обозначим эти случайные численности каждой стороны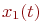 
и 
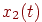соответственно. Тогда:
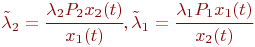
Зависимость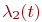 
и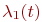 
от случайных значени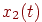й и 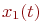делает аналитическое решение задачи практически невозможным. Поэтому, используя принцип квазирегулярности, заменим 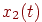и 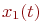их матожиданиям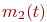и 
и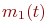 
.
Заметим, что 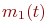и 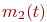являются целью моделирования.
После замены выражения для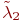 
и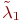 
принимают вид:
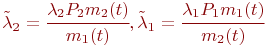
Запишем уравнения динамики средних для состояни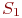й 
и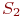 
:
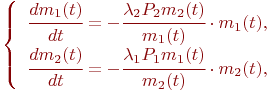
Для состояни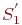й 
и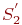 
уравнения не нужны, так как средние численности этих состояни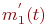й 
и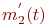 
однозначно связаны с 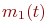и :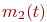
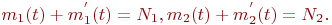
После очевидного упрощения уравнения динамики средних принимают вид:
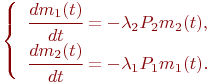
Здесь и далее для лучшей обозримости аргумент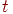 
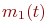в и 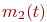опустим.
Систему уравнений (2.3) обычно называют уравнениями динамики боя, иногда - уравнениями Ланчестера. Ланчестер - полковник английской армии времен первой мировой войны. Именно он предложил излагаемые подходы формализации боевых действий.
Date: 2015-07-17; view: 522; Нарушение авторских прав