
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дополнительные курсы 2 page
|
|
| . Лекция: Типовые математические модели: версия для печати и PDA В лекции рассматриваются элементы теории марковских процессов и ряд аналитических моделей, в основе которых лежит допущение о марковости протекающих в моделируемых объектах процессов. | ||

| ||

| ||

| ||
Во многих случаях модель может быть представлена в виде конструкций из математических символов. В первой теме такие модели мы назвали аналитическими, чтобы отделить от других математических моделей - имитационных. С развитием последних область применения аналитических моделей сократилась. Однако актуальность такого моделирования сохраняется для систем, особенно тех, в которых протекают так называемые процессы без последействия. Процессы без последействия находят место при функционировании многих технических систем. Впервые один из типов такого процесса ввел в научный обиход и исследовал отечественный математик А. А. Марков, поэтому процессы без последействия и системы, в которых они протекают, названы марковскими, а один из типов такого процесса назван цепью Маркова. В настоящее время теория марковских процессов разработана широко и детально, в основном, благодаря отечественным ученым А. Я. Хинчину, Б. В. Гнеденко, А. Н. Колмогорову и другим. Популярность этой теории состоит еще и в том, что она может быть применена и к системам с последействием, которые с помощью некоторых ухищрений можно трактовать как марковские.
В этой теме рассматриваются элементы теории марковских процессов и ряд аналитических моделей, в основе которых лежит допущение о марковости протекающих в моделируемых объектах процессов. К таковым, в первую очередь, относится широкий класс самых разнообразных объектов, имеющих общее название систем массового обслуживания (СМО). Для ряда стандартных структур СМО аналитические модели, связывающие показатели эффективности СМО с характеристиками элементов СМО, приведены в соответствующих справочниках. Здесь же приводятся классификация СМО и приемы построения графов состояний СМО, позволяющих строить или применять готовые аналитические модели.
Заметим, что для ряда современных сложных СМО аналитическое моделирование неприемлемо в силу недостаточности адекватных математических средств. В этих случаях следует применять имитационное моделирование, которое детально рассматривается в следующих темах.
В многоэлементных системах с большим числом состояний аналитическое моделирование на основе теории марковских процессов становится весьма громоздким. В этом случае используется так называемый метод динамики средних, который в основе имеет также марковость процесса. Этот метод существенно упрощает аналитическое моделирование для случаев определения средних характеристик состояний моделируемой системы. В этой теме дано обоснование метода и приводятся примеры его применения.
2.1. Дискретные марковские процессы
Наиболее полное исследование процесса функционирования систем получается, если известны явные математические зависимости, связывающие искомые показатели с начальными условиями, параметрами и переменными исследуемой системы. Для многих современных систем, являющихся объектами моделирования, такие математические зависимости отсутствуют или малопригодны, и следует применять другое моделирование, как правило, имитационное.
Однако есть ряд конкретных математических схем, проверенных практикой и доказавших эффективность моделированием. Целью изучения настоящей темы является освоение таких математических моделей.
В инженерно практике часто возникает задача моделирования процессов случайной смены состояний в исследуемом объекте. В рамках нашей профессии нас интересуют дискретные состояния. Например, техническое состояние объекта может характеризоваться дискретными состояниями: исправен - неисправен, загружен - находится в простое и т. п. Численности боевых средств противоборствующих сторон изменяются дискретно, очереди объектов, ожидающих обслуживания, и многое другое.
Вид очередного состояния может определяться случайным образом, смена состояний может происходить в случайные или не случайные моменты времени.
Большой класс случайных процессов составляют процессы без последействия, которые в математике называют марковскими процессами в честь Андрея Андреевича Маркова - старшего (1856 - 1922), выдающегося русского математика, разработавшего основы теории таких процессов.
Сущность процесса без последействия понятна из определения.
Случайный процесс называется марковским, если вероятность перехода системы в новое состояние зависит только от состояния системы в настоящий момент и не зависит от того, когда и каким образом система перешла в это состояние.
Практически любой случайный процесс является марковским или может быть сведен к марковскому. В последнем случае достаточно в понятие состояния включить всю предысторию смен состояний системы.
А. А. Марков имеет дополнение к фамилии "старший" потому, что его сын - тоже Андрей Андреевич Марков - выдающийся математик, специалист в области теории алгоритмов и др.
А. А. Марков - старший известен также как давший вероятностное обоснование метода наименьших квадратов, приведший одно из доказательств предельной теоремы теории вероятностей и многое другое.
Дальнейшее развитие теория марковских процессов получила в работах выдающегося отечественного математика Андрея Николаевича Колмогорова.
Марковские процессы делятся на два класса:
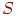 имеет имеет 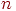 возможных состояний: возможных состояний: 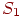 , , 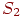 ,..., ,..., 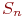 . Вообще говоря, число состояний может быть бесконечным. Однако модель, как правило, строится для конечного числа состояний.
Смена состояний происходит, будем считать, мгновенно и в строго определенные моменты времени . Вообще говоря, число состояний может быть бесконечным. Однако модель, как правило, строится для конечного числа состояний.
Смена состояний происходит, будем считать, мгновенно и в строго определенные моменты времени 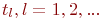 В дальнейшем будем называть временные точки В дальнейшем будем называть временные точки 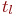 шагами.
Известны вероятности перехода шагами.
Известны вероятности перехода 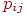 системы за один шаг из состояния системы за один шаг из состояния 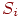 в состояние в состояние 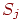 .
Цель моделирования: определить вероятности состояний системы после .
Цель моделирования: определить вероятности состояний системы после 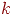 -го шага.
Обозначим эти вероятности -го шага.
Обозначим эти вероятности 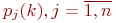 (не путать с вероятностями (не путать с вероятностями 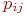 ).
Если в системе отсутствует последействие, то есть вероятности ).
Если в системе отсутствует последействие, то есть вероятности 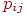 не зависят от предыстории нахождения системы в состоянии не зависят от предыстории нахождения системы в состоянии 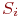 , а определяются только этим состоянием, то описанная ситуация соответствует модели дискретной марковской цепи.
Марковская цепь называется однородной, если переходные вероятности , а определяются только этим состоянием, то описанная ситуация соответствует модели дискретной марковской цепи.
Марковская цепь называется однородной, если переходные вероятности 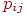 от времени не зависят, то есть от шага к шагу не меняются. В противном случае, то есть если переходные вероятности от времени не зависят, то есть от шага к шагу не меняются. В противном случае, то есть если переходные вероятности 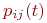 зависят от времени, марковская цепь называется неоднородной.
Значения зависят от времени, марковская цепь называется неоднородной.
Значения 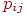 обычно сводятся в матрицу переходных вероятностей: обычно сводятся в матрицу переходных вероятностей:
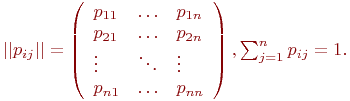 Значения
Значения 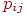 могут также указываться на графе состояний системы. На рис. 2.1 показан размеченный граф для четырех состояний системы. Обычно вероятности переходов "в себя" - могут также указываться на графе состояний системы. На рис. 2.1 показан размеченный граф для четырех состояний системы. Обычно вероятности переходов "в себя" - 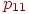 , , 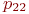 и т. д. на графе состояний можно не проставлять, так как их значения дополняют до 1 сумму переходных вероятностей, указанных на ребрах (стрелках), выходящих из данного состояния.
Не указываются также нулевые вероятности переходов. Например, на рис. 2.1 это вероятности и т. д. на графе состояний можно не проставлять, так как их значения дополняют до 1 сумму переходных вероятностей, указанных на ребрах (стрелках), выходящих из данного состояния.
Не указываются также нулевые вероятности переходов. Например, на рис. 2.1 это вероятности 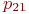 , , 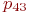 и др.
Математической моделью нахождения вероятностей состояний однородной марковской цепи является рекуррентная зависимость и др.
Математической моделью нахождения вероятностей состояний однородной марковской цепи является рекуррентная зависимость
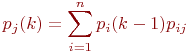 где
где 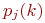 - вероятность - вероятность 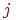 -го состояния системы после -го состояния системы после 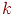 -го шага, -го шага, 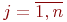 ; ;
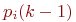 - вероятность - вероятность 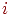 -го состояния системы после -го состояния системы после  -го шага, -го шага, 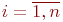 ; ;
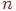 - число состояний системы; - число состояний системы;
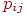 -переходные вероятности. -переходные вероятности.
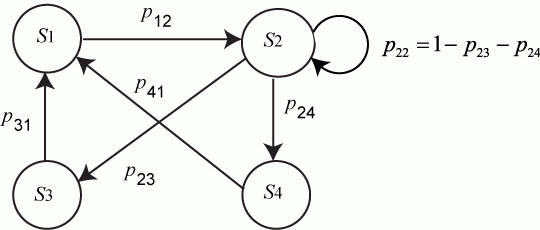 Рис. 2.1. Размеченный граф состояний системы
Для неоднородной марковской цепи вероятности состояний системы находятся по формуле:
Рис. 2.1. Размеченный граф состояний системы
Для неоднородной марковской цепи вероятности состояний системы находятся по формуле:
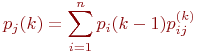 где
где 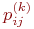 - значения переходных вероятностей для - значения переходных вероятностей для 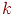 -го шага.
Пример 2.1. По группе из четырех объектов производится три последовательных выстрела. Найти вероятности состояний группы объектов после третьего выстрела.
Матрица переходных вероятностей имеет вид: -го шага.
Пример 2.1. По группе из четырех объектов производится три последовательных выстрела. Найти вероятности состояний группы объектов после третьего выстрела.
Матрица переходных вероятностей имеет вид:
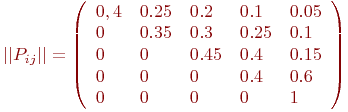 Размеченный граф состояний приведен на рис. 2.2.
Размеченный граф состояний приведен на рис. 2.2.
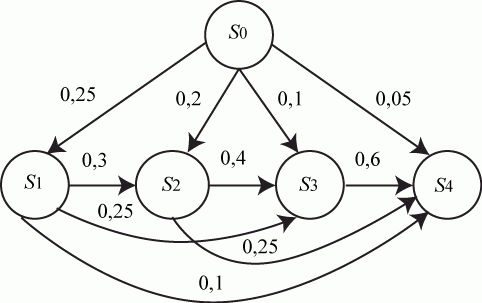 Рис. 2.2. Размеченный граф состояний четырех объектов
Прежде чем приступить к вычислениям необходимо, ответить на следующие вопросы.
Рис. 2.2. Размеченный граф состояний четырех объектов
Прежде чем приступить к вычислениям необходимо, ответить на следующие вопросы.
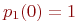 .
После первого выстрела все значения вероятностей .
После первого выстрела все значения вероятностей 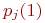 соответствуют первой строке матрицы переходных вероятностей. Рассчитаем вероятности остальных состояний. соответствуют первой строке матрицы переходных вероятностей. Рассчитаем вероятности остальных состояний.
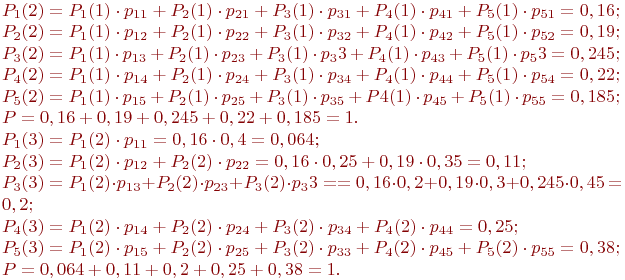 Сформулируем методику моделирования по схеме дискретных марковских процессов (марковских цепей).
Сформулируем методику моделирования по схеме дискретных марковских процессов (марковских цепей).
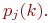 При неоднородном марковском процессе переходная вероятность
При неоднородном марковском процессе переходная вероятность 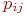 представляет собой условную вероятность перехода представляет собой условную вероятность перехода
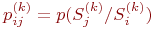 , зависящую от , зависящую от 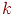 - очередного временного шага. В этом случае должны быть указаны более одной матрицы значений - очередного временного шага. В этом случае должны быть указаны более одной матрицы значений 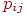 (для некоторых шагов матрицы могут быть одинаковыми).
Например, при нанесении ударов по объектам, которые могут перемещаться (танковая группировка, корабли и т. п.), последние будут принимать меры по рассредоточению средств или другому защитному маневру, вплоть до активного противодействия атакующей стороне. Очевидно, все эти меры приведут к уменьшению поражающих возможностей стороны, наносящей удары, т. е. к соответствующему изменению переходных вероятностей. Процесс становится неоднородным.
2.2. Моделирование по схеме непрерывных марковских процессов
Cyщecтвyeт широкий класс систем, которые меняют свои состояния в случайные моменты времени (для некоторых шагов матрицы могут быть одинаковыми).
Например, при нанесении ударов по объектам, которые могут перемещаться (танковая группировка, корабли и т. п.), последние будут принимать меры по рассредоточению средств или другому защитному маневру, вплоть до активного противодействия атакующей стороне. Очевидно, все эти меры приведут к уменьшению поражающих возможностей стороны, наносящей удары, т. е. к соответствующему изменению переходных вероятностей. Процесс становится неоднородным.
2.2. Моделирование по схеме непрерывных марковских процессов
Cyщecтвyeт широкий класс систем, которые меняют свои состояния в случайные моменты времени 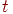 . Как и в предыдущем случае, в этих системах рассматривается процесс с дискретными состояниями . Как и в предыдущем случае, в этих системах рассматривается процесс с дискретными состояниями 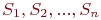 . Например, переход объекта от исправного состояния к неисправному, соотношение сил сторон в ходе боя и т. п. Оценка эффективности таких систем определяется с помощью вероятностей каждого состояния . Например, переход объекта от исправного состояния к неисправному, соотношение сил сторон в ходе боя и т. п. Оценка эффективности таких систем определяется с помощью вероятностей каждого состояния 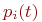 на любой момент времени на любой момент времени 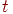 , , 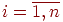 .
Чтобы определить вероятности состояния системы .
Чтобы определить вероятности состояния системы 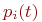 для любого момента времени для любого момента времени 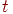 необходимо воспользоваться математическими моделями марковских процессов с непрерывным временем (непрерывных марковских процессов).
При моделировании состояния систем с непрерывными марковскими процессами мы уже не можем воспользоваться переходными вероятностями необходимо воспользоваться математическими моделями марковских процессов с непрерывным временем (непрерывных марковских процессов).
При моделировании состояния систем с непрерывными марковскими процессами мы уже не можем воспользоваться переходными вероятностями 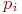 , так как вероятность "перескока" системы из одного состояния в другое точно в момент времени , так как вероятность "перескока" системы из одного состояния в другое точно в момент времени 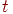 равна нулю (как вероятность любого отдельного значения непрерывной случайной величины).
Поэтому вместо переходных вероятностей вводятся в рассмотрение плотности вероятностей переходов равна нулю (как вероятность любого отдельного значения непрерывной случайной величины).
Поэтому вместо переходных вероятностей вводятся в рассмотрение плотности вероятностей переходов 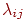 : :
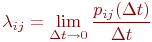 где
где 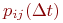 - вероятность того, что система, находившаяся в момент времени - вероятность того, что система, находившаяся в момент времени 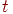 в состоянии в состоянии 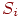 за время за время 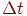 перейдет в состояние перейдет в состояние 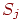 .
С точностью до бесконечно малых второго порядка из приведенной формулы можно представить: .
С точностью до бесконечно малых второго порядка из приведенной формулы можно представить:
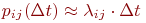 Непрерывный марковский процесс называется однородным, если плотности вероятностей переходов
Непрерывный марковский процесс называется однородным, если плотности вероятностей переходов 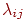 не зависят от времени не зависят от времени 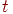 (от момента начала промежутка (от момента начала промежутка 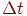 ). В противном случае непрерывный марковский процесс называется неоднородным.
Целью моделирования, как и в случае дискретных процессов, является определение вероятностей состояний системы ). В противном случае непрерывный марковский процесс называется неоднородным.
Целью моделирования, как и в случае дискретных процессов, является определение вероятностей состояний системы  . Эти вероятности находятся интегрированием системы дифференциальных уравнений Колмогорова.
Сформулируем методику моделирования по схеме непрерывных марковских процессов. . Эти вероятности находятся интегрированием системы дифференциальных уравнений Колмогорова.
Сформулируем методику моделирования по схеме непрерывных марковских процессов.
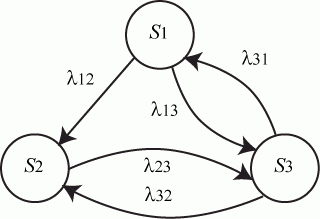 Рис. 2.3. Размеченный граф состояний
Решение
Рис. 2.3. Размеченный граф состояний
Решение
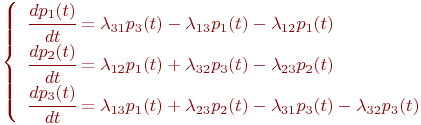 Очевидно,
Очевидно,  .
Поэтому любое из первых трех уравнений можно исключить, как линейно зависимое.
Для решения уравнений Колмогорова необходимо задать начальные условия. Для рассмотренного примера 2.2, можно задать такие начальные условия: .
Поэтому любое из первых трех уравнений можно исключить, как линейно зависимое.
Для решения уравнений Колмогорова необходимо задать начальные условия. Для рассмотренного примера 2.2, можно задать такие начальные условия: 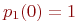 , , 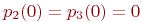 .
Однородный марковский процесс с непрерывным временем можно трактовать как процесс смены состояний под влиянием некоторого потока событий. То есть плотность вероятности перехода можно трактовать как интенсивность потока событий, переводящих систему из .
Однородный марковский процесс с непрерывным временем можно трактовать как процесс смены состояний под влиянием некоторого потока событий. То есть плотность вероятности перехода можно трактовать как интенсивность потока событий, переводящих систему из 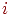 -го состояния в -го состояния в 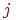 -е. Такими потоками событий являются отказы техники, вызовы на телефонной станции, рождение и т. п.
При исследовании сложных объектов всегда интересует: возможен ли в исследуемой системе установившейся (стационарный) режим? То есть, как ведет себя система при -е. Такими потоками событий являются отказы техники, вызовы на телефонной станции, рождение и т. п.
При исследовании сложных объектов всегда интересует: возможен ли в исследуемой системе установившейся (стационарный) режим? То есть, как ведет себя система при 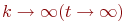 ? Существуют ли предельные значения ? Существуют ли предельные значения 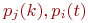 ? Как правило, именно эти предельные значения интересуют исследователя.
Ответ на данный вопрос дает теорема Маркова.
Если для однородного дискретного марковского процесса с конечным или счетным числом состояний все ? Как правило, именно эти предельные значения интересуют исследователя.
Ответ на данный вопрос дает теорема Маркова.
Если для однородного дискретного марковского процесса с конечным или счетным числом состояний все 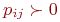 , то предельные значения , то предельные значения 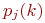 существуют и их значения не зависят от выбранного начального состояния системы.
Применительно к непрерывным марковским процессам теорема Маркова трактуется так: если процесс однородный и из каждого состояния возможен переход за конечное время в любое другое состояние и число состояний счетно или конечно, то предельные значения существуют и их значения не зависят от выбранного начального состояния системы.
Применительно к непрерывным марковским процессам теорема Маркова трактуется так: если процесс однородный и из каждого состояния возможен переход за конечное время в любое другое состояние и число состояний счетно или конечно, то предельные значения  существуют и их значения не зависят от выбранного начального состояния.
Например (рис. 2.4), в системе А стационарный режим есть, а в системе В стационарного режима нет: если система окажется в состоянии существуют и их значения не зависят от выбранного начального состояния.
Например (рис. 2.4), в системе А стационарный режим есть, а в системе В стационарного режима нет: если система окажется в состоянии  она не сможет перейти ни в какое другое состояние. она не сможет перейти ни в какое другое состояние.
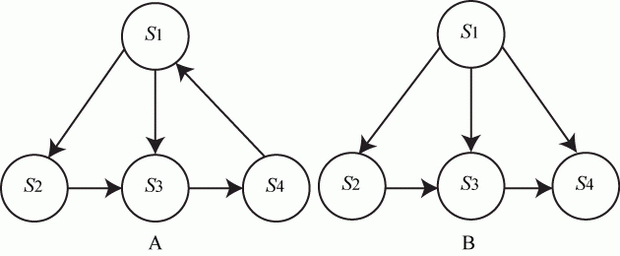 увеличить изображение Рис. 2.4. Примеры графов состояний систем с различными режимами
2.3. Схема гибели и размножения
Часто в системах самого различного назначения протекают процессы, которые можно представить в виде модели "гибели и размножения".
Граф состояний такого процесса показан на рис. 2.5.
увеличить изображение Рис. 2.4. Примеры графов состояний систем с различными режимами
2.3. Схема гибели и размножения
Часто в системах самого различного назначения протекают процессы, которые можно представить в виде модели "гибели и размножения".
Граф состояний такого процесса показан на рис. 2.5.
 увеличить изображение Рис. 2.5. Схема "гибели и размножения"
Особенностью модели является наличие прямой и обратной связей с каждым соседним состоянием для всех средних состояний; первое и последнее (крайние) состояния связаны только с одним "соседом" (с последующим и предыдущим состояниями соответственно).
Название модели - "гибель и размножение" - связано с представлением, что стрелки вправо означают переход к состояниям, связанным с ростом номера состояния ("рождение"), а стрелки влево - с убыванием номера состояний ("гибель").
Очевидно, стационарное состояние в этом процессе существует. Составлять уравнения Колмогорова нет необходимости, так как структура регулярна, необходимые формулы приводятся в справочниках, а также в рекомендованной литературе.
Для приведенных на рис. 2.4 обозначений формулы имеют вид:
увеличить изображение Рис. 2.5. Схема "гибели и размножения"
Особенностью модели является наличие прямой и обратной связей с каждым соседним состоянием для всех средних состояний; первое и последнее (крайние) состояния связаны только с одним "соседом" (с последующим и предыдущим состояниями соответственно).
Название модели - "гибель и размножение" - связано с представлением, что стрелки вправо означают переход к состояниям, связанным с ростом номера состояния ("рождение"), а стрелки влево - с убыванием номера состояний ("гибель").
Очевидно, стационарное состояние в этом процессе существует. Составлять уравнения Колмогорова нет необходимости, так как структура регулярна, необходимые формулы приводятся в справочниках, а также в рекомендованной литературе.
Для приведенных на рис. 2.4 обозначений формулы имеют вид:
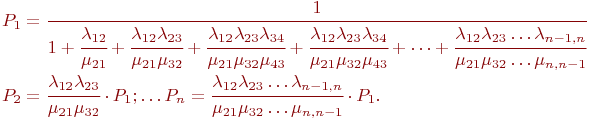 Пример 2.3. Имеется система из двух одинаковых и работающих параллельно компьютеров.
Требуется определить надежностные характеристики этой системы.
Решение
В этой системе возможны три состояния:
Пример 2.3. Имеется система из двух одинаковых и работающих параллельно компьютеров.
Требуется определить надежностные характеристики этой системы.
Решение
В этой системе возможны три состояния:
 - оба компьютера исправны; - оба компьютера исправны;
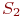 - один компьютер исправен, другой ремонтируется; - один компьютер исправен, другой ремонтируется;
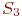 - оба компьютера неисправны и ремонтируются. Будем полагать, что процессы отказов и восстановлений - однородные марковские, одновременный выход из строя обоих компьютеров, как и одновременное восстановление двух отказавших компьютеров практически невозможно.
Поскольку компьютеры одинаковые, то с точки зрения надежности, неважно, какой именно компьютер неисправен в состоянии - оба компьютера неисправны и ремонтируются. Будем полагать, что процессы отказов и восстановлений - однородные марковские, одновременный выход из строя обоих компьютеров, как и одновременное восстановление двух отказавших компьютеров практически невозможно.
Поскольку компьютеры одинаковые, то с точки зрения надежности, неважно, какой именно компьютер неисправен в состоянии 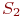 , важно, что один.
С учетом сказанного, ситуация моделируется схемой "гибели и размножения" (рис. 2.6). , важно, что один.
С учетом сказанного, ситуация моделируется схемой "гибели и размножения" (рис. 2.6).
 Рис. 2.6.
На рис. 2.6:
Рис. 2.6.
На рис. 2.6:
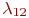 , , 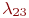 - интенсивности потоков отказов; - интенсивности потоков отказов;
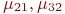 - интенсивности потоков восстановлений.
Пусть среднее время безотказной работы каждого компьютера - интенсивности потоков восстановлений.
Пусть среднее время безотказной работы каждого компьютера
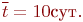 , а среднее время восстановления одного компьютера , а среднее время восстановления одного компьютера 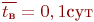 .
Тогда интенсивность отказов одного компьютера будет равна .
Тогда интенсивность отказов одного компьютера будет равна 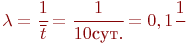 , а интенсивность восстановления одного компьютера - , а интенсивность восстановления одного компьютера - 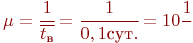 .
В состоянии .
В состоянии  работают оба компьютера, следовательно: работают оба компьютера, следовательно:
 В состоянии
В состоянии 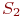 работает один компьютер, значит: работает один компьютер, значит:
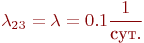 В состоянии
В состоянии 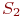 восстанавливается один компьютер, тогда: восстанавливается один компьютер, тогда:
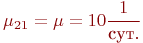 В состоянии
В состоянии 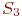 восстанавливаются оба компьютера: восстанавливаются оба компьютера:
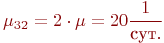 Используем зависимости (2.2). Вероятность состояния, когда обе машины исправны:
Используем зависимости (2.2). Вероятность состояния, когда обе машины исправны:
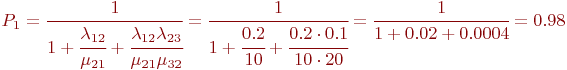 Вероятность второго состояния
Вероятность второго состояния 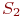 (работает один компьютер): (работает один компьютер):
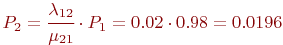 Аналогично вычисляется и
Аналогично вычисляется и 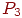 . Хотя найти . Хотя найти 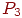 можно и так: можно и так:
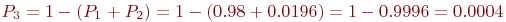 Пример 2.4. В полосе объединения работают передатчики противника. Подразделение операторов-связистов армейской контрразведки ведет поиск передатчиков по их радиоизлучениям. Каждый оператор, обнаружив передатчик противника, следит за его частотой, при этом новым поиском не занимается. В процессе слежения частота может быть потеряна, после чего оператор снова осуществляет поиск.
Разработать математическую модель для определения эффективности службы подразделения операторов. Под эффективностью понимается среднее число обнаруженных передатчиков за установленный промежуток времени.
Решение
Будем считать, что наши операторы и радисты противника обладают высокой квалификацией, хорошо натренированы. Следовательно, можно принять, что интенсивности обнаружения частот передатчиков противника и потерь слежения - постоянны. Обнаружение частоты и ее потеря зависят только от того, сколько запеленговано передатчиков в настоящий момент и не зависят от того, когда произошло это пеленгование. Следовательно, процесс обнаружения и потерь слежения за частотами можно считать непрерывным однородным марковским процессом.
Исследуемое свойство этой системы пеленгации: загруженность операторов, что, очевидно, совпадает с числом обнаруженных частот.
Введем обозначения:
Пример 2.4. В полосе объединения работают передатчики противника. Подразделение операторов-связистов армейской контрразведки ведет поиск передатчиков по их радиоизлучениям. Каждый оператор, обнаружив передатчик противника, следит за его частотой, при этом новым поиском не занимается. В процессе слежения частота может быть потеряна, после чего оператор снова осуществляет поиск.
Разработать математическую модель для определения эффективности службы подразделения операторов. Под эффективностью понимается среднее число обнаруженных передатчиков за установленный промежуток времени.
Решение
Будем считать, что наши операторы и радисты противника обладают высокой квалификацией, хорошо натренированы. Следовательно, можно принять, что интенсивности обнаружения частот передатчиков противника и потерь слежения - постоянны. Обнаружение частоты и ее потеря зависят только от того, сколько запеленговано передатчиков в настоящий момент и не зависят от того, когда произошло это пеленгование. Следовательно, процесс обнаружения и потерь слежения за частотами можно считать непрерывным однородным марковским процессом.
Исследуемое свойство этой системы пеленгации: загруженность операторов, что, очевидно, совпадает с числом обнаруженных частот.
Введем обозначения:
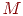 - количество операторов; - количество операторов;
 - количество передатчиков противника, полагаем - количество передатчиков противника, полагаем 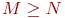 ; ;
 - среднее число операторов, ведущих слежение; - среднее число операторов, ведущих слежение;
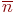 - среднее число запеленгованных передатчиков; - среднее число запеленгованных передатчиков;
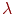 - интенсивность пеленгации передатчика противника одним оператором; - интенсивность пеленгации передатчика противника одним оператором;
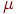 - интенсивность потока потерь слежения оператором; - интенсивность потока потерь слежения оператором;
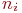 - текущая численность запеленгованных передатчиков - текущая численность запеленгованных передатчиков 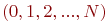 .
В системе пеленгации возможны следующие состояния: .
В системе пеленгации возможны следующие состояния:
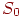 - запеленгованных передатчиков нет, поиск ведут - запеленгованных передатчиков нет, поиск ведут 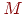 операторов, вероятность состояния операторов, вероятность состояния 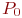 ; ;
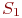 - запеленгован 1 передатчик, поиск ведут - запеленгован 1 передатчик, поиск ведут 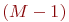 операторов, вероятность состояния операторов, вероятность состояния 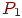 ; ;
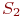 - запеленгованы 2 передатчика, поиск ведут - запеленгованы 2 передатчика, поиск ведут 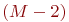 операторов, вероятность состояния операторов, вероятность состояния 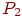 ;
… ;
…
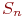 - запеленгованы - запеленгованы 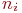 передатчиков, вероятность передатчиков, вероятность 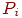 ;
… ;
…
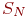 - запеленгованы - запеленгованы  передатчиков, вероятность передатчиков, вероятность 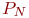 .
Цель моделирования - .
Цель моделирования - 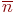 - достигается вычислением: - достигается вычислением:
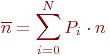 Как и в примере 2.3 полагаем, что одновременное обнаружение или потеря двух и более частот практически невозможно. Граф состояний системы показан на рис. 2.7.
Как и в примере 2.3 полагаем, что одновременное обнаружение или потеря двух и более частот практически невозможно. Граф состояний системы показан на рис. 2.7.
 увеличить изображение Рис. 2.7. Граф состояний системы пеленгации
Граф соответствует процессу "гибели и размножения", полносвязный, число состояний системы, конечно, значит, установившийся режим, и предельные значения вероятностей в системе пеленгации существуют.
Пусть, к примеру, количество операторов
увеличить изображение Рис. 2.7. Граф состояний системы пеленгации
Граф соответствует процессу "гибели и размножения", полносвязный, число состояний системы, конечно, значит, установившийся режим, и предельные значения вероятностей в системе пеленгации существуют.
Пусть, к примеру, количество операторов  , а количество передатчиков противника , а количество передатчиков противника 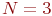 . В этом случае граф состояний имеет вид (рис. 2.8): . В этом случае граф состояний имеет вид (рис. 2.8):
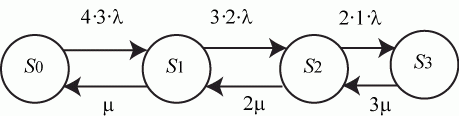 Рис. 2.8. Вариант графа состояний системы пеленгации
Для упрощения вычислений примем
Рис. 2.8. Вариант графа состояний системы пеленгации
Для упрощения вычислений примем 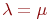 . Тогда для этой схемы "гибели и размножения" по зависимостям (2.2) имеем: . Тогда для этой схемы "гибели и размножения" по зависимостям (2.2) имеем:
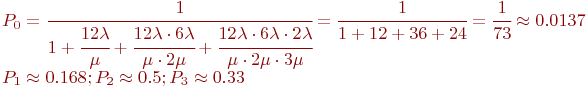 Окончательно:
Окончательно:
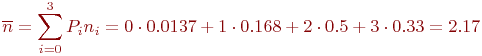 Таким образом, в условиях данного примера в среднем будут пеленговаться не менее двух передатчиков противника.
Непрерывный марковский процесс полностью определяется значениями плотностей вероятностей переходов
Таким образом, в условиях данного примера в среднем будут пеленговаться не менее двух передатчиков противника.
Непрерывный марковский процесс полностью определяется значениями плотностей вероятностей переходов 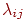 , , 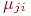 .Ранее был установлен их физический смысл как интенсивности потоков событий, переводящих систему из одного состояния в другое. Поток событий в однородных непрерывных марковских процессах характеризуется экспоненциальным законом распределения случайных интервалов времени между событиями. Такой поток называют простейшим или стационарным пуассоновским.
Простейший поток обладает свойствами: .Ранее был установлен их физический смысл как интенсивности потоков событий, переводящих систему из одного состояния в другое. Поток событий в однородных непрерывных марковских процессах характеризуется экспоненциальным законом распределения случайных интервалов времени между событиями. Такой поток называют простейшим или стационарным пуассоновским.
Простейший поток обладает свойствами:
 увеличить изображение Рис. 2.9. Система массового обслуживания
Элементами СМО являются:
увеличить изображение Рис. 2.9. Система массового обслуживания
Элементами СМО являются:
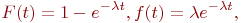 здесь
здесь 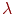 - интенсивность потока.
Название потока - пуассоновский - происходит от того, что для этого потока вероятность - интенсивность потока.
Название потока - пуассоновский - происходит от того, что для этого потока вероятность 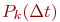 появления появления 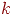 заявок за интервал заявок за интервал 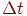 определяется законом Пуассона: определяется законом Пуассона:
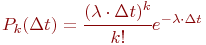 Поток такого типа, как отмечалось ранее, называют также простейшим. Именно такой поток предполагают проектировщики при разработке СМО. Вызвано это тремя причинами.
Во-первых, поток этого типа в теории массового обслуживания аналогичен нормальному закону распределения в теории вероятностей в том смысле, что к простейшему потоку приводит предельный переход для потока, являющегося суммой потоков с произвольными характеристиками при бесконечном увеличении слагаемых и уменьшении их интенсивности. То есть сумма произвольных независимых (без преобладания) потоков с интенсивностями
Поток такого типа, как отмечалось ранее, называют также простейшим. Именно такой поток предполагают проектировщики при разработке СМО. Вызвано это тремя причинами.
Во-первых, поток этого типа в теории массового обслуживания аналогичен нормальному закону распределения в теории вероятностей в том смысле, что к простейшему потоку приводит предельный переход для потока, являющегося суммой потоков с произвольными характеристиками при бесконечном увеличении слагаемых и уменьшении их интенсивности. То есть сумма произвольных независимых (без преобладания) потоков с интенсивностями 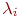 является простейшим потоком с интенсивностью является простейшим потоком с интенсивностью
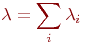 Во-вторых, если обслуживающие каналы (приборы) рассчитаны на простейший поток заявок, то обслуживание других типов потоков (с той же интенсивностью) будет обеспечено с не меньшей эффективностью.
В-третьих, именно такой поток определяет марковский процесс в системе и, следовательно, простоту аналитического анализа системы. При других потоках анализ функционирования СМО сложен.
Часто встречаются системы, у которых поток входных заявок зависит от количества заявок, находящихся в обслуживании. Такие СМО называют замкнутыми(иначе - разомкнутыми). Например, работа мастерской связи объединения может быть представлена моделью замкнутой СМО. Пусть эта мастерская предназначена для обслуживания радиостанций, которых в объединении
Во-вторых, если обслуживающие каналы (приборы) рассчитаны на простейший поток заявок, то обслуживание других типов потоков (с той же интенсивностью) будет обеспечено с не меньшей эффективностью.
В-третьих, именно такой поток определяет марковский процесс в системе и, следовательно, простоту аналитического анализа системы. При других потоках анализ функционирования СМО сложен.
Часто встречаются системы, у которых поток входных заявок зависит от количества заявок, находящихся в обслуживании. Такие СМО называют замкнутыми(иначе - разомкнутыми). Например, работа мастерской связи объединения может быть представлена моделью замкнутой СМО. Пусть эта мастерская предназначена для обслуживания радиостанций, которых в объединении  . Каждая из них имеет интенсивность отказов . Каждая из них имеет интенсивность отказов  . Входной поток отказавшей аппаратуры будет иметь интенсивность . Входной поток отказавшей аппаратуры будет иметь интенсивность 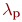 : :
 где
где 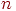 - количество радиостанций, уже находящихся в мастерской на ремонте.
Заявки могут иметь разные права на начало обслуживания. В этом случае говорят, что заявки неоднородные. Преимущества одних потоков заявок перед другими задаются шкалой приоритетов.
Важной характеристикой входного потока является коэффициент вариации: - количество радиостанций, уже находящихся в мастерской на ремонте.
Заявки могут иметь разные права на начало обслуживания. В этом случае говорят, что заявки неоднородные. Преимущества одних потоков заявок перед другими задаются шкалой приоритетов.
Важной характеристикой входного потока является коэффициент вариации:
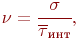 где
где  - математическое ожидание длины интервала; - математическое ожидание длины интервала;
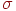 - среднеквадратическое отклонение случайной величины (длины интервала) - среднеквадратическое отклонение случайной величины (длины интервала)  .
Для простейшего потока .
Для простейшего потока 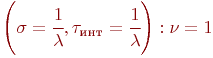 Для большинства реальных потоков
Для большинства реальных потоков 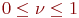 .
При .
При 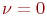 поток регулярный, детерминированный.
Коэффициент вариации - характеристика, отражающая степень неравномерности поступления заявок.
Каналы (приборы) обслуживания. В СМО могут быть один или несколько обслуживающих приборов (каналов). Согласно с этим СМО называют одноканальными или многоканальными.
МногоканальныеСМО могут состоять из однотипных или разнотипных приборов. Обслуживающими приборами могут быть: поток регулярный, детерминированный.
Коэффициент вариации - характеристика, отражающая степень неравномерности поступления заявок.
Каналы (приборы) обслуживания. В СМО могут быть один или несколько обслуживающих приборов (каналов). Согласно с этим СМО называют одноканальными или многоканальными.
МногоканальныеСМО могут состоять из однотипных или разнотипных приборов. Обслуживающими приборами могут быть:
 где
где 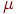 - интенсивность обслуживания, - интенсивность обслуживания, 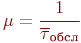 ; ;
 - математическое ожидание времени обслуживания.
То есть процесс обслуживания - марковский, а это, как теперь нам известно, дает существенные удобства в аналитическом математическом моделировании.
Кроме экспоненциального встречаются - математическое ожидание времени обслуживания.
То есть процесс обслуживания - марковский, а это, как теперь нам известно, дает существенные удобства в аналитическом математическом моделировании.
Кроме экспоненциального встречаются  -распределение Эрланга, гиперэкспоненциальное, треугольное и некоторые другие. Это нас не должно смущать, так как показано, что значение критериев эффективности СМО мало зависят от вида закона распределения вероятностей времени обслуживания.
При исследовании СМО выпадает из рассмотрения сущность обслуживания, качество обслуживания.
Каналы могут быть абсолютно надежными, то есть не выходить из строя. Вернее, так может быть принято при исследовании. Каналы могут обладать конечной надежностью. В этом случае модель СМО значительно сложнее.
Очередь заявок. В силу случайного характера потоков заявок и обслуживания пришедшая заявка может застать канал (каналы) занятым обслуживанием предыдущей заявки. В этом случае она либо покинет СМО не обслуженной, либо останется в системе, ожидая начало своего обслуживания. В соответствии с этим различают: -распределение Эрланга, гиперэкспоненциальное, треугольное и некоторые другие. Это нас не должно смущать, так как показано, что значение критериев эффективности СМО мало зависят от вида закона распределения вероятностей времени обслуживания.
При исследовании СМО выпадает из рассмотрения сущность обслуживания, качество обслуживания.
Каналы могут быть абсолютно надежными, то есть не выходить из строя. Вернее, так может быть принято при исследовании. Каналы могут обладать конечной надежностью. В этом случае модель СМО значительно сложнее.
Очередь заявок. В силу случайного характера потоков заявок и обслуживания пришедшая заявка может застать канал (каналы) занятым обслуживанием предыдущей заявки. В этом случае она либо покинет СМО не обслуженной, либо останется в системе, ожидая начало своего обслуживания. В соответствии с этим различают:
 .
Исследователя обычно интересуют такие статистические характеристики, связанные с пребыванием заявок в очереди: .
Исследователя обычно интересуют такие статистические характеристики, связанные с пребыванием заявок в очереди:
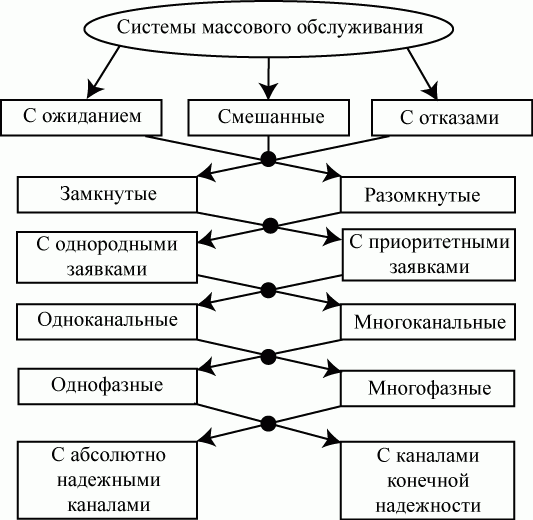 Рис. 2.10. Классификация СМО
Для обозначения простых (однофазных) СМО используется символика, предложенная Кендаллом:
Рис. 2.10. Классификация СМО
Для обозначения простых (однофазных) СМО используется символика, предложенная Кендаллом:
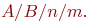
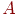 - входящий поток заявок: - входящий поток заявок: 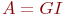 - рекуррентный поток; - рекуррентный поток; 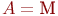 - простейший поток с показательным законом распределения вероятностей; - простейший поток с показательным законом распределения вероятностей; 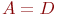 - регулярный или детерминированный поток (с постоянными интервалами между моментами поступления заявок). - регулярный или детерминированный поток (с постоянными интервалами между моментами поступления заявок).
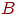 - случайная длительность обслуживания: - случайная длительность обслуживания: 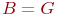 или или 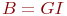 - рекуррентное обслуживание с одной и той же функцией распределения - рекуррентное обслуживание с одной и той же функцией распределения 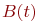 для разных каналов; для разных каналов; 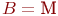 - показательное обслуживание; - показательное обслуживание; 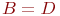 - регулярное обслуживание. - регулярное обслуживание.
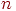 - количество обслуживающих каналов. Если - количество обслуживающих каналов. Если 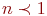 , то система называется многоканальной. , то система называется многоканальной.
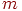 - количество мест для ожидания заявок в очереди. Если - количество мест для ожидания заявок в очереди. Если 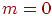 , то СМО с потерями (без ожидания); , то СМО с потерями (без ожидания); 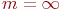 - система с неограниченным ожиданием; - система с неограниченным ожиданием; 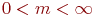 - система с ограниченным числом мест для ожидания.
2.5. Моделирование СМО в классе непрерывных марковских процессов
Под операцией в СМО понимают комплекс мероприятий по обслуживанию входящего потока заявок на интервале времени - система с ограниченным числом мест для ожидания.
2.5. Моделирование СМО в классе непрерывных марковских процессов
Под операцией в СМО понимают комплекс мероприятий по обслуживанию входящего потока заявок на интервале времени 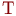 .
В зависимости от типа системы показателями исхода операции или эффективности системы массового обслуживания являются следующие.
Для СМО с отказами: .
В зависимости от типа системы показателями исхода операции или эффективности системы массового обслуживания являются следующие.
Для СМО с отказами:
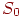 - все инспекторы свободны; - все инспекторы свободны;
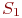 - занят один инспектор; - занят один инспектор;
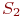 - заняты два инспектора; - заняты два инспектора;
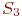 - заняты три инспектора.
Граф состояний системы приведен на рис. 2.11. - заняты три инспектора.
Граф состояний системы приведен на рис. 2.11.
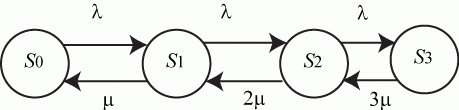 Рис. 2.11. Граф состояний трехканальной СМО с отказами
На графе:
Рис. 2.11. Граф состояний трехканальной СМО с отказами
На графе: 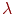 - интенсивность потока грузовых автомобилей; - интенсивность потока грузовых автомобилей; 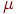 - интенсивность проверок документов одним автоинспектором.
Моделирование проводится с целью определения части автомобилей, которые не будут проверены.
Решение.
Искомая часть вероятности - интенсивность проверок документов одним автоинспектором.
Моделирование проводится с целью определения части автомобилей, которые не будут проверены.
Решение.
Искомая часть вероятности 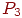 - вероятности занятости всех трех инспекторов. Поскольку граф состояний представляет типовую схему "гибели и размножения", то найдем - вероятности занятости всех трех инспекторов. Поскольку граф состояний представляет типовую схему "гибели и размножения", то найдем 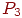 , используя зависимости (2.2). , используя зависимости (2.2).
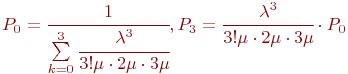 Пропускную способность этого поста автоинспекторов можно характеризовать относительной пропускной способностью:
Пропускную способность этого поста автоинспекторов можно характеризовать относительной пропускной способностью:
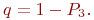 Пример 2.6. Для приема и обработки донесений от разведгруппы в разведотделе объединения назначена группа в составе трех офицеров. Ожидаемая интенсивность потока донесений - 15 донесений в час. Среднее время обработки одного донесения одним офицером -
Пример 2.6. Для приема и обработки донесений от разведгруппы в разведотделе объединения назначена группа в составе трех офицеров. Ожидаемая интенсивность потока донесений - 15 донесений в час. Среднее время обработки одного донесения одним офицером - 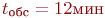 . Каждый офицер может принимать донесения от любой разведгруппы. Освободившийся офицер обрабатывает последнее из поступивших донесений. Поступающие донесения должны обрабатываться с вероятностью не менее 95 %.
Определить, достаточно ли назначенной группы из трех офицеров для выполнения поставленной задачи.
Решение
Группа офицеров работает как СМО с отказами, состоящая из
трех каналов. Поток донесений с интенсивностью . Каждый офицер может принимать донесения от любой разведгруппы. Освободившийся офицер обрабатывает последнее из поступивших донесений. Поступающие донесения должны обрабатываться с вероятностью не менее 95 %.
Определить, достаточно ли назначенной группы из трех офицеров для выполнения поставленной задачи.
Решение
Группа офицеров работает как СМО с отказами, состоящая из
трех каналов. Поток донесений с интенсивностью 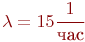 можно считать простейшим, так как он суммарный от нескольких разведгрупп. Интенсивность обслуживания можно считать простейшим, так как он суммарный от нескольких разведгрупп. Интенсивность обслуживания 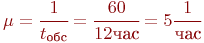 . Закон распределения неизвестен, но это несущественно, так как показано, что для систем с отказами он может быть произвольным.
Описание состояний и граф состояний СМО будут аналогичны приведенным в примере 2.5.
Поскольку граф состояний - это схема "гибели и размножения", то для нее имеются готовые выражения для предельных вероятностей состояния: . Закон распределения неизвестен, но это несущественно, так как показано, что для систем с отказами он может быть произвольным.
Описание состояний и граф состояний СМО будут аналогичны приведенным в примере 2.5.
Поскольку граф состояний - это схема "гибели и размножения", то для нее имеются готовые выражения для предельных вероятностей состояния:
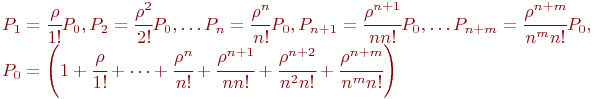 Отношение
Отношение 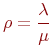 называют приведенной интенсивностью потока заявок. Физический смысл ее следующий: величина называют приведенной интенсивностью потока заявок. Физический смысл ее следующий: величина  представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.
В примере представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.
В примере 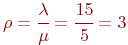 .
В рассматриваемой СМО отказ наступает при занятости всех трех каналов, то есть .
В рассматриваемой СМО отказ наступает при занятости всех трех каналов, то есть 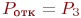 . Тогда: . Тогда:
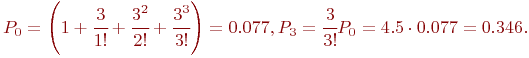 Так как вероятность отказа в обработке донесений составляет более 34 % (
Так как вероятность отказа в обработке донесений составляет более 34 % ( ), то необходимо увеличить личный состав группы. Увеличим состав группы в два раза, то есть СМО будет иметь теперь шесть каналов, и рассчитаем ), то необходимо увеличить личный состав группы. Увеличим состав группы в два раза, то есть СМО будет иметь теперь шесть каналов, и рассчитаем 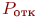 : :
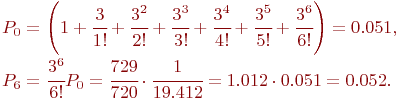 Теперь
Теперь 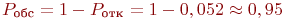 .
Таким образом, только группа из шести офицеров сможет обрабатывать поступающие донесения с вероятностью 95 %.
2.5.2. Многоканальная СМО с ожиданием
Пример 2.7. На участке форсирования реки имеются 15 однотипных переправочных средств. Поток поступления техники на переправу в среднем составляет 1 ед./мин, среднее время переправы одной единицы техники - 10 мин (с учетом возвращения назад переправочного средства).
Оценить основные характеристики переправы, в том числе вероятность в немедленной переправе сразу по прибытии единицы техники.
Решение .
Таким образом, только группа из шести офицеров сможет обрабатывать поступающие донесения с вероятностью 95 %.
2.5.2. Многоканальная СМО с ожиданием
Пример 2.7. На участке форсирования реки имеются 15 однотипных переправочных средств. Поток поступления техники на переправу в среднем составляет 1 ед./мин, среднее время переправы одной единицы техники - 10 мин (с учетом возвращения назад переправочного средства).
Оценить основные характеристики переправы, в том числе вероятность в немедленной переправе сразу по прибытии единицы техники.
Решение
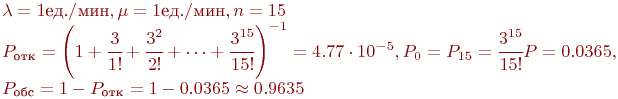 Абсолютная пропускная способность
Абсолютная пропускная способность 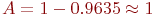 , т. е. все, что подходит к переправе, тут же практически переправляется.
Среднее число работающих переправочных средств: , т. е. все, что подходит к переправе, тут же практически переправляется.
Среднее число работающих переправочных средств:
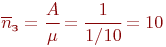 Коэффициенты использования и простоя переправы:
Коэффициенты использования и простоя переправы:
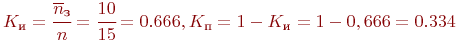 Для решения примера была также разработана программа. Интервалы времени поступления техники на переправу, время переправы приняты распределенными по экспоненциальному закону.
Коэффициенты использования переправы после 50 прогонов практически совпадают:
Для решения примера была также разработана программа. Интервалы времени поступления техники на переправу, время переправы приняты распределенными по экспоненциальному закону.
Коэффициенты использования переправы после 50 прогонов практически совпадают: 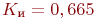 .
Максимальная длина очереди 15 ед., среднее время пребывания в очереди около 10 мин.
Если взять число переправочных средств 10, то коэффициент использования близок к 1 ( .
Максимальная длина очереди 15 ед., среднее время пребывания в очереди около 10 мин.
Если взять число переправочных средств 10, то коэффициент использования близок к 1 (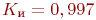 ), максимальная длина очереди - 43 единицы техники.
2.5.3. Одноканальная СМО с ограниченной очередью
Если в очереди ), максимальная длина очереди - 43 единицы техники.
2.5.3. Одноканальная СМО с ограниченной очередью
Если в очереди 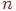 мест для ожидания, то система может находиться в одном из следующих мест для ожидания, то система может находиться в одном из следующих  состояний: состояний:
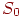 - в системе нет заявок (ни в очереди, ни на обслуживании); - в системе нет заявок (ни в очереди, ни на обслуживании);
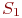 - в системе обслуживается одна заявка, очередь пуста; - в системе обслуживается одна заявка, очередь пуста;
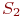 - в системе обслуживается одна заявка, и одна заявка находится в очереди, ожидает обслуживания;
… - в системе обслуживается одна заявка, и одна заявка находится в очереди, ожидает обслуживания;
…
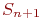 - в системе обслуживается одна заявка и - в системе обслуживается одна заявка и 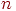 заявок находятся в очереди, ожидают обслуживания.
Граф состояний такой системы представляет схему "гибели и размножения" (рис. 2.12). заявок находятся в очереди, ожидают обслуживания.
Граф состояний такой системы представляет схему "гибели и размножения" (рис. 2.12).
 Рис. 2.12. Граф состояний одноканальной СМО с ограниченной очередью
2.5.4. Одноканальная замкнутая СМО
Опишем состояния одноканальной замкнутой СМО.
Рис. 2.12. Граф состояний одноканальной СМО с ограниченной очередью
2.5.4. Одноканальная замкнутая СМО
Опишем состояния одноканальной замкнутой СМО.
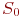 - заявок на обслуживание нет. - заявок на обслуживание нет.
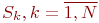 - на обслуживании находится - на обслуживании находится 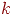 заявок; заявок;
 - общее число заявок, циркулирующих в системе; - общее число заявок, циркулирующих в системе;
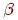 - интенсивность требований на обслуживание от одной заявки.
Граф состояний одноканальной замкнутой СМО приведен на рис. 2.13. Модель данной СМО также представляет "схему гибели и размножения". - интенсивность требований на обслуживание от одной заявки.
Граф состояний одноканальной замкнутой СМО приведен на рис. 2.13. Модель данной СМО также представляет "схему гибели и размножения".
 увеличить изображение Рис. 2.13. Граф состояний одноканальной замкнутой СМО
Однако не менее часто модель СМО не сводится к схеме "гибели и размножения". Например, в СМО с конечной надежностью каналов обслуживания.
2.5.5. Одноканальная СМО с конечной надежностью
Построить граф состояний одноканальной СМО с очередью на три заявки и с конечной надежностью каналов обслуживания. При отказе канала обслуживания заявка, находившаяся на обслуживании, теряется. Процессы в системе - марковские.
Описание состояний СМО:
увеличить изображение Рис. 2.13. Граф состояний одноканальной замкнутой СМО
Однако не менее часто модель СМО не сводится к схеме "гибели и размножения". Например, в СМО с конечной надежностью каналов обслуживания.
2.5.5. Одноканальная СМО с конечной надежностью
Построить граф состояний одноканальной СМО с очередью на три заявки и с конечной надежностью каналов обслуживания. При отказе канала обслуживания заявка, находившаяся на обслуживании, теряется. Процессы в системе - марковские.
Описание состояний СМО:
 - состояния исправной СМО; - состояния исправной СМО;
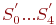 - состояния неисправной СМО.
Обозначения: - состояния неисправной СМО.
Обозначения:
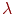 - интенсивность поступления заявок; - интенсивность поступления заявок;
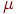 - интенсивность обработки заявки каналом; - интенсивность обработки заявки каналом;
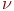 - интенсивность поломок канала; - интенсивность поломок канала;
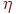 - интенсивность ремонта неисправного канала.
Граф состояний СМО с конечной надежностью каналов обслуживания приведен на рис. 2.14. - интенсивность ремонта неисправного канала.
Граф состояний СМО с конечной надежностью каналов обслуживания приведен на рис. 2.14.
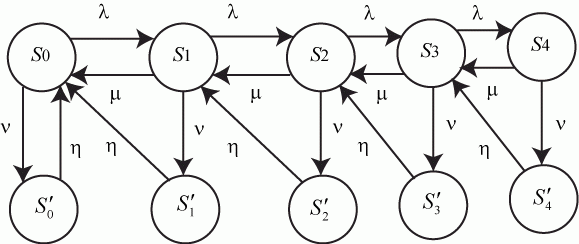 Рис. 2.14. Граф состояний СМО с конечной надежностью
Если в состоянии
Рис. 2.14. Граф состояний СМО с конечной надежностью
Если в состоянии  (канал свободен, в очереди заявок нет) система выйти из строя не может, то состояния (канал свободен, в очереди заявок нет) система выйти из строя не может, то состояния  нет. Так как при отказе заявка, находившаяся на обслуживании, теряется, то после восстановления переход осуществляется к предыдущему состоянию, например, из состояния нет. Так как при отказе заявка, находившаяся на обслуживании, теряется, то после восстановления переход осуществляется к предыдущему состоянию, например, из состояния 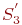 в состояние в состояние 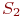 .
Эта модель не является моделью "гибели и размножения". Поэтому соответствующие вероятности находятся решением системы линейных алгебраических уравнений, полученных из уравнений Колмогорова для стационарного режима.
2.6. Метод динамики средних. Сущность и содержание метода
В многоэлементных системах часто целью моделирования является определение средних количеств элементов, находящихся в одинаковых состояниях.
Например, в задаче о пеленгации передатчиков противника командира интересует число запеленгированных передатчиков, а не вероятности пеленгации одного передатчика, двух, трех и т. д. Но чтобы определить среднее число их, надо знать вероятности всех возможных состояний .
Эта модель не является моделью "гибели и размножения". Поэтому соответствующие вероятности находятся решением системы линейных алгебраических уравнений, полученных из уравнений Колмогорова для стационарного режима.
2.6. Метод динамики средних. Сущность и содержание метода
В многоэлементных системах часто целью моделирования является определение средних количеств элементов, находящихся в одинаковых состояниях.
Например, в задаче о пеленгации передатчиков противника командира интересует число запеленгированных передатчиков, а не вероятности пеленгации одного передатчика, двух, трех и т. д. Но чтобы определить среднее число их, надо знать вероятности всех возможных состояний 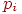 , так как , так как
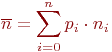 Но число состояний и, следовательно, число уравнений Колмогорова может оказаться настолько большим, что вызовет непреодолимые трудности при моделировании по схеме марковских процессов.
Например, в соединении имеется 100 радиостанций. Каждая из них может находиться в боевых условиях в пяти состояниях:
Но число состояний и, следовательно, число уравнений Колмогорова может оказаться настолько большим, что вызовет непреодолимые трудности при моделировании по схеме марковских процессов.
Например, в соединении имеется 100 радиостанций. Каждая из них может находиться в боевых условиях в пяти состояниях:
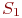 - исправна, работает, не обнаружена; - исправна, работает, не обнаружена;
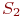 - исправна, работает, обнаружена; - исправна, работает, обнаружена;
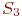 - работоспособна, но подавлена помехами; - работоспособна, но подавлена помехами;
 - обнаружена, поражена; - обнаружена, поражена;
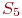 - находится в ремонте;
Для определения средних численностей каждого из этих состояний пришлось бы составить - находится в ремонте;
Для определения средних численностей каждого из этих состояний пришлось бы составить 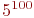 уравнений Колмогорова. Очевидно, такое моделирование не годится.
В исследовании операций есть метод, позволяющий успешно решать такие и аналогичные задачи. Этот метод называется метод динамики средних.
Метод динамики средних позволяет непосредственно определять математическое ожидание числа элементов сложной системы, находящихся в одинаковых состояниях.
Метод дает приближенные результаты. Но обладает замечательным свойством: чем больше система имеет элементов и состояний, тем точнее результат математического моделирования.
Для получения расчетных формул метода предположим, что имеем дело с системой, обладающей следующими признаками: уравнений Колмогорова. Очевидно, такое моделирование не годится.
В исследовании операций есть метод, позволяющий успешно решать такие и аналогичные задачи. Этот метод называется метод динамики средних.
Метод динамики средних позволяет непосредственно определять математическое ожидание числа элементов сложной системы, находящихся в одинаковых состояниях.
Метод дает приближенные результаты. Но обладает замечательным свойством: чем больше система имеет элементов и состояний, тем точнее результат математического моделирования.
Для получения расчетных формул метода предположим, что имеем дело с системой, обладающей следующими признаками:
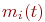 , находящихся в одинаковых состояниях , находящихся в одинаковых состояниях 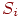 , и дисперсию , и дисперсию 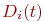 .
Схематично такая система может быть представлена так, как показано на рис. 2.15.
Система имеет .
Схематично такая система может быть представлена так, как показано на рис. 2.15.
Система имеет  элементов, а каждый элемент имеет элементов, а каждый элемент имеет 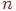 состояний. Численность состояний. Численность 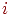 -го состояния на любой момент вр -го состояния на любой момент вр Date: 2015-07-17; view: 1245; Нарушение авторских прав |

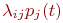 и
и 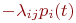 . Число произведений столько, сколько стрелок связано с данным состоянием. Если стрелка графа направлена в данное состояние, то соответствующее произведение имеет знак плюс, если из данного состояния - минус.
. Число произведений столько, сколько стрелок связано с данным состоянием. Если стрелка графа направлена в данное состояние, то соответствующее произведение имеет знак плюс, если из данного состояния - минус. 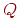 )- среднее число заявок, обслуживаемое системой за время
)- среднее число заявок, обслуживаемое системой за время 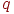 )- средняя доля поступивших заявок, обслуживаемая системой (отношение среднего числа обслуженных заявок к среднему числу поступивших за время
)- средняя доля поступивших заявок, обслуживаемая системой (отношение среднего числа обслуженных заявок к среднему числу поступивших за время 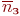 );
); 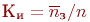 , где
, где 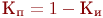 .
. 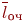 );
); 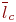 );
); 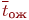 );
); 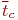 );
);  );
); 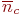 ,
,