Пример выполнения контрольной работы № 2

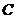
1. Получим поэлементное описание, которое включает компонентные и топологические уравнения.

Компонентными уравнениями для элементов R,C,Lявляются следующие уравнения:

_r (1)

(2)

(3)

Составим топологические уравнения:

Так как все элементы соединены последовательно, можно записать

i_r = i _c= i_l (4)

Напряжение на входе U₂

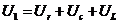(5)

Напряжение на выходе U₂

(6)

2. Получим вход-выходное описание – математическую модель, связывающую входной сигнал U₁ и выходной сигнал U₂.

Перепишем уравнение (5) c учетом уравнения (1)

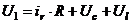
Продифференцируем данное уравнение по t, получим:

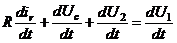(7)

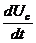заменим с учетом уравнения (2) на

заменим с учетом уравнений (4), (3) и (6)

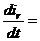
(8)

Тогда уравнение 7 перепишем в виде:

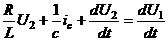
Для того чтобы избавиться от тока i_c продифференцируем уравнение еще раз:

(9)

с учетом уравнения (8) уравнение (9) примет вид:

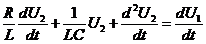- вход-выходное описание в форме дифференциального уравнения.

В операторной форме:

3. Получим передаточную функцию используя уравнение в операторной форме.

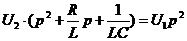
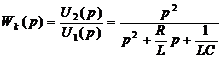
- передаточная функция ЭКУ (10)

4. Получим математическую модель в пространстве состояний.

Введем вектор переменных состояний:

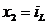
Получим выражения для 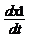, , 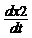зависящие от х₁, х₂ и входного сигнала U(t).

Для этого используем формулу (5) для напряжений по контуру:

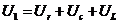
Выразим U_r, U_c, U_l через переменные состояния х_1, х₂

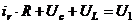
х₂ R + x₁ + L = U₁

Выразим :

=

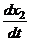Уравнение (2) с учетом переменных состояния примет вид:

Из уравнений (5) и (6) с учетом переменных состояний получим уравнение выхода:

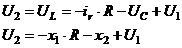
В матричном виде модель в пространстве состояний примет вид:

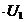- уравнение динамики (11)

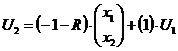- уравнение выхода (12)

5.Оценим устойчивость, управляемость, наблюдаемость ЭКУ.

Выберем значения R=10 кОм, L=250 мГн, C=1 мкФ и подставим их в выражение (10) для передаточной функции:

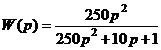(13)

Для расчетов используем MatLab.

Введем полином знаменателя:

» p=[250 10 1]

p =

250 10 1

Для оценки устойчивости вычислим корни характеристического уравнения:

» rt=roots(p)

rt =

-0.0200 + 0.0600i

-0.0200 - 0.0600i

Вещественные части корней характеристического уравнения имеют отрицательные знаки, следовательно, система устойчива.

Для оценки управляемости используем модель в пространстве состояний. Построим матрицу управляемости R:

R=[B A*B]

Вводим матрицу А

» a=[0 1/1;-1/250 -1/(250*10)]

Вводим матрицу В

» b=[0;1/250]

Вычисляем матрицу R:

» r=[b a*b ]

Определяем ранг матрицы:

» rg=rank(r)

rg = 2

Ранг матрицы R равен n, следовательно система управляема.

Для оценки наблюдаемости системы, построим матрицу наблюдаемости Q:

Q=[C^T A^T* C^T]

Построим транспонированную матрицу А:

» at=a'

Вводим матрицу С:

» c=[-1 -10]

Построим транспонированную матрицу С:

» ct=c'

Вычисляем матрицу наблюдаемости Q:

» q=[ct at*ct ]

Определяем ранг матрицы:

» rg=rank(q)

rg = 2

Ранг матрицы Q равен n, следовательно, система наблюдаема.

6. Построим граф системы:

-10

-1

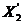
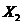
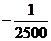
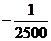
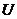
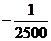
Рис. 12. Граф системы

Граф системы построим по полученной модели в пространстве состояний (11), (12):

7. Построим графики АЧХ, ФЧХ, годограф АФЧХ, переходную характеристику.

Введем передаточную функцию (13):

» w=tf([250 0 0],[250 10 1])

Transfer function:

250 s^2

------------------

250 s^2 + 10 s + 1

Графики АЧХ и ФЧХ строятся по введенной передаточной функции командой bode.

>> bode(w)

Рис. 13. Частотные характеристики ЛФЧХ и ЛАЧХ

График АФЧХ строится по передаточной функции командой nyquist.

>> nyquist(w)

Рис. 14. АФЧХ

Построим переходную характеристику ЭКУ с помощью команды step:

» step(w)

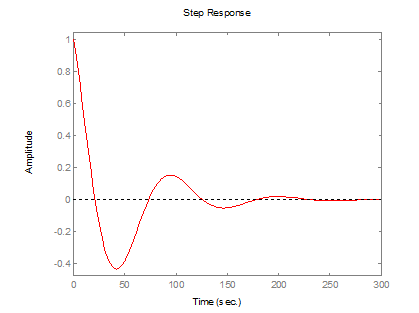
Рис. 15. Переходная характеристика h(t)

По переходной характеристике определим время переходного процесса – 135с.

8. Заключение: таким образом, исследуемая система оказалась устойчивой, управляемой, наблюдаемой, время переходного процесса составляет 135 с.

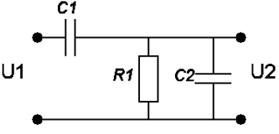
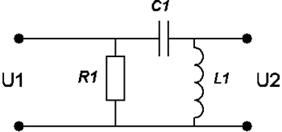
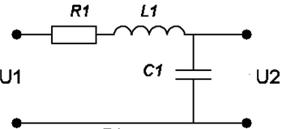
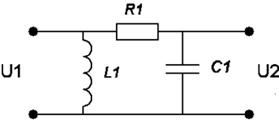
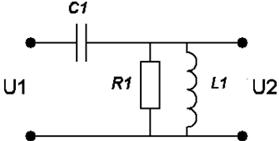
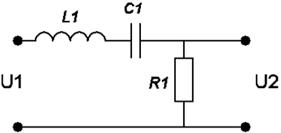
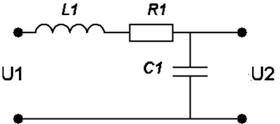
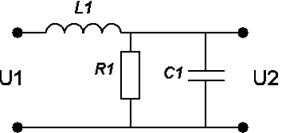
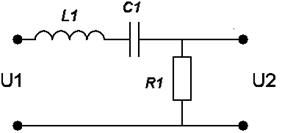
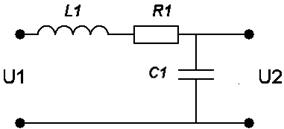
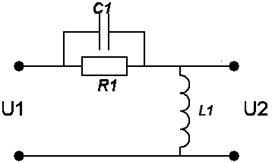
Варианты заданий:

№ вари-анта	Схема	№ вари-анта	Схема

Литература

1. Асанов А.З. Моделирование и анализ динамических систем. – Набережные Челны: Изд-во КамПИ, 2003. – 152с.

2. Асанов А.З. Цифровое моделирование и анализ динамических систем. Лабораторный практикум. - Набережные Челны: Изд-во КамПИ, 2004. – 105с.

3. Ахмадеев И.А. Теория автоматического управления. Использование системы MATLAB для исследования систем автоматического управления. Лабораторный практикум.- Набережные Челны: Изд-во КамПИ, 2002. – 46с.

Содержание

1. Краткие теоретические сведения............................................................................................ 3

2. Контрольная работа № 1......................................................................................................... 15

3. Контрольная работа № 2......................................................................................................... 25

Литература................................................................................................................................... 33

Date: 2015-07-17; view: 437; Нарушение авторских прав