
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Изучение коэффициентов корреляции Спирмена и Кэнделла. Пусть некоторые объекты обладают парой признаков каждый и гипотеза об их взаимосвязи не отвергается
|
|
Пусть некоторые объекты обладают парой признаков каждый и гипотеза об их взаимосвязи не отвергается. Если признаки оказались взаимосвязаны, исследователя интересует сила их связи. Для описания такой связи было предложено много различных коэффициентов, называемых мерами связи.
В порядковых (ординальных) шкалах реальным содержанием измерений является тот порядок, в котором выстраиваются объекты (по степени выраженности измеряемого признака) и вместо значений чисел рассматривают их ранги. Здесь проверка нулевой гипотезы ведётся методом Спирмена. Пусть признаков два и каждый из n объектов характеризуется парой чисел (xi, yj) - своими значениями признаков А и В. От чисел переходим к их рангам (ri, sj). Cчитаем, что среди чисел xi и yj нет повторяющихся. Если признаки взаимосвязаны, то порядок, в котором следуют числа xi влияет на порядок, в котором следуют числа yj. Чем более тесно связаны эти признаки, тем в большей степени последовательность ri предопределяет последовательность sj. Если же признаки такой связи не проявляют, то порядок среди игреков случаен по отношению к порядку среди иксов. В этом случае все n! перестановок чисел 1, 2,..., n, которые могут выступать как ранги, оказываются равновероятными при любом порядке чисел ri. По предложению Спирмена, близость двух рядов рангов ri и sj можно характеризовать статистикой:

Она принимает наименьшее возможное значение S = 0 тогда и только тогда, когда последовательности полностью совпадают. Наибольшее возможное значение величина S принимает, когда эти последовательности полностью противоположны. При этом искомая сумма есть сумма квадратов последовательных нечётных чисел:
Smax = (n - 1)² + [(n - 1) - 2)]² +… + 1² = (n³ - n)/3
Принято, что коэффициент корреляции должен изменяться от (-1) до 1. Поэтому нормированный и центрированный коэффициент связи Спирмена:
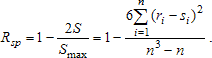
Крайние значения ±1 он принимает в случаях полной предсказуемости одной ранговой последовательности по другой. Значение S не зависит от первоначальной нумерации объектов. Поэтому обычно упорядочивают данные по одному из признаков. Последовательность рангов по этому признаку: 1, 2,..., n.
Другой коэффициент ранговой корреляции получил популярность после работ М. Кендэлла. В качестве меры сходства между двумя ранжировками, используется минимальное число перестановок соседних объектов, которые надо сделать, чтобы одно упорядочение объектов превратить в другое. Пусть один ряд упорядочен, а второй состоит из чисел sj. Тогда K равно числу инверсий в последовательности {sj}. Пусть, например, n = 4 и (sj) = (4, 3, 1, 2). Инверсии (нарушения порядка) суть:
- первый элемент последовательности дает три инверсии: 4 прежде 3, 4 прежде 1, 4 прежде 2. - второй элемент дает три инверсии: 3 прежде 1, 3 прежде 2.
Всего инверсий в данном случае K = 5 = 3 + 2.
Наименьшее возможное значение K = 0, наибольшее K = n(n - 1)/2. Как и для S, эти значения получаются при полном совпадении и полной противоположности ранговых последовательностей. Коэффициент ранговой корреляции по Кендэллу:
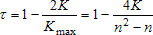
Распределение обоих коэффициентов корреляции строится при нулевой гипотезе, когда все n! возможных значений расположений рангов {sj} равновероятны. Составлены таблицы. Для небольших n эти таблицы точные, для других значений - приближенные. Если Н0 верна, распределение коэффициентов симметрично и концентрируется около нуля тем сильнее, чем больше n. Если признаки зависимы, распределение вероятностей может быть иным. Поведение коэффициентов ранговой корреляции в этом случае легко проследить лишь для наиболее простого вида связи - монотонной (положительной или отрицательной). Для монотонной положительной связи значение одного признака тем больше, чем больше значение другого. При отрицательной - наоборот. Такая альтернатива независимости легко обнаруживается с помощью коэффициента ранговой корреляции, абсолютное значение которого в этом случае должно быть близко к единице. Если же зависимость между признаками более сложная, ее влияние на ранжировки может быть не столь простым. Поэтому с помощью коэффициентов ранговой корреляции далеко не всякую зависимость можно отличить от независимости. Все же появление в эксперименте больших (по модулю) наблюдаемых значений коэффициентов ранговой корреляции свидетельствует против гипотезы независимости в пользу связи между признаками (положительной либо отрицательной, смотря по знаку коэффициента). Для проверки Н0 надо вычислить выборочное значение коэффициента ранговой корреляции и сравнить его с критическим значением для данного уровня значимости, которое следует извлечь из таблиц. Гипотезу Н0 надо отвергнуть (на выбранном уровне значимости), если полученное в опыте значение коэффициента ранговой корреляции превосходит критическое (по модулю). При больших n и при Н0 нормированные статистики распределены (приближенно) по стандартному нормальному закону:
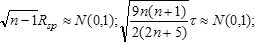
Пример задания по теме Корреляционный анализ
Корреляционный анализ изучает стохастические связи между случайными величинами в экономике. Метод корреляции применяется для того, чтобы при сложном взаимодействии посторонних влияний выявить зависимость между результатом и факторами в том случае, если посторонние факторы не изменялись и не искажали основную зависимость. При этом число наблюдений должно быть достаточно велико, так как малое число наблюдений не позволяет обнаружить закономерность связи. Укрупненно можно рекомендовать: число наблюдений равно восьмикратному числу факторов, включенных в модель.
Задание:
1.) Построить корреляционное поле зависимости между y и x1. Сделать вывод относительно формы и направления связи.
2.) Построить уравнение регрессии между у и х1 (линейная, степенная, логарифмическая). Оценить каждую функцию через F-критерий, 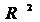 , ошибку аппроксимации.
, ошибку аппроксимации.
3.) Построить корреляционное поле зависимости между y и x2. Сделать вывод относительно формы и направления связи.
4.) Построить двухфакторное уравнение регрессии между y, x1,x2. Оценить показатели тесноты связи.
5.) Оценить модель через F-критерий Фишера.
6.) Оценить параметры через t-критерий Стьюдента.
Исходные данные:
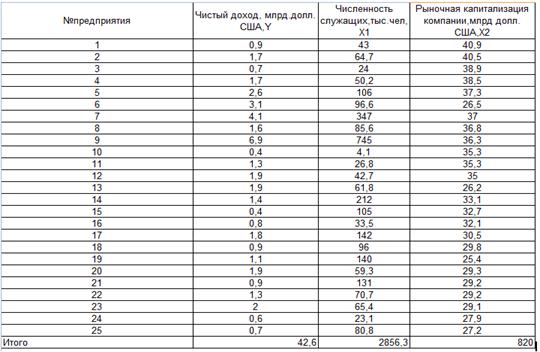
Уравнение регрессии между у и х1 (линейная):
F расч = (0,7451/(1-0,7451))*((25-1-1)/1) = 67,232
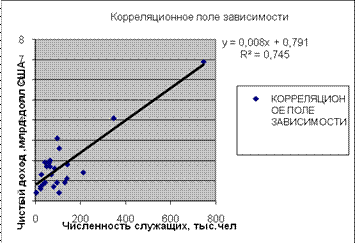
Уравнение регрессии между у и х1 (логарифмическая):
F расч = (0,4445/(1-0,4445))*((25-1-1)/1) = 18,404
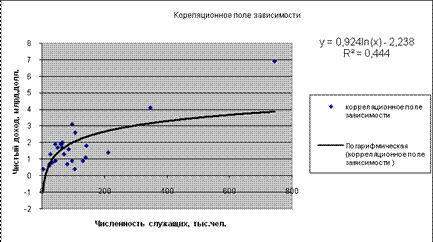
Уравнение регрессии между у и х1 (степенная):
F расч = (0,4284/(1-0,4284))*((25-1-1)/1) = 0,019
| линейная | F расч | 67,23146332 |
| логарифмическая | F расч | 18,40414041 |
| степенная | F расч | 0,019459742 |
| Е1 | 53,9 |
| Е2 | 72,5 |
| Е3 | 48,2 |
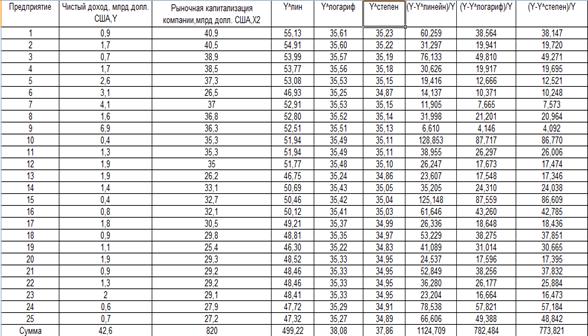
Уравнение регрессии между у и х2 (линейная):
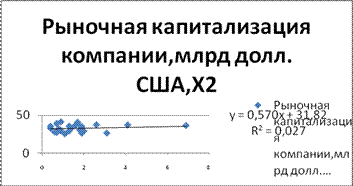
Уравнение регрессии между у и х2(логарифмическая):

Уравнение регрессии между у и х2(степенная):
| E1 | |
| E2 | |
| E3 |
С помощью пакета анализа
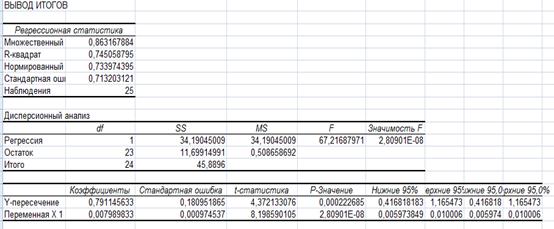
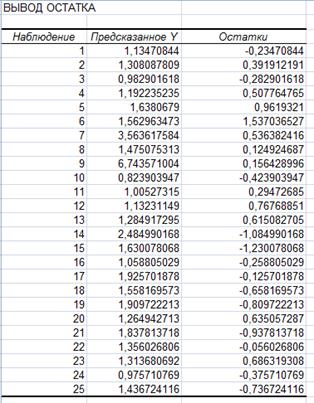
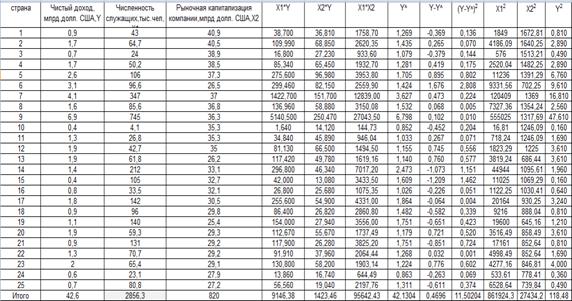
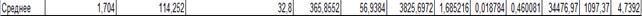
| Y=0,148+0,008*x1+0,019*x2 |
| r yx1 | 0,863 |
| ryx2 | 0,005 |
| rx1x2 | 0,395 |
| r yx1x2 | 0,937 |
| ryx2x1 | -0,723 |
| rx1x2y | 0,772 |
| R yx1x2 | 0,937 |
| R^2 yx1x2 | 0,878 |
| сигма ост | 0,003 |
| Fрасч | 72,08 |
| Fтабл | 2,086 |
| стьюдента | 34,40 |
Линейный коэффициент корреляции может быть определен по формуле:
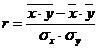
Или

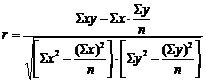 .
.
Он изменяется в диапазоне от -1 до +1. положительный коэффициент характеризует прямую связь, отрицательный – обратную. Связь между факторным и результативным признаком можно признать тесной, если r>0,7.
Индекс корреляции может рассчитываться по формуле:
 ,
,
Индекс корреляции изменяется от 0 до 1.
оценка существенности связи на основе t – критерия Стьюдента (при оценке параметров) или F – критерия Фишера (при оценке уравнения регрессии).
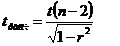 для линейной формы связи,
для линейной формы связи,
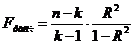 для криволинейной формы связи,
для криволинейной формы связи,
где k – число параметров.
Нахождение аппроксимирующего уравнения, для чего определяется средняя ошибка аппроксимации
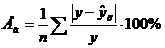 .
.
F -критерия Фишера:

Date: 2015-07-17; view: 600; Нарушение авторских прав