Построение многофакторных моделей. Отбор факторов

Построение моделей множественной регрессии включает несколько этапов:

-Выбор формы связи (уравнения регрессии).

-Отбор факторных признаков.

-Обеспечение достаточного объема совокупности.

Важным этапом построения уже выбранного уравнения множественной регрессии является отбор и последующее включение факторных признаков.

С одной стороны, чем больше факторных признаков включено в уравнение, тем оно лучше описывает явление. Однако модель размерностью 100 и более факторных признаков сложно реализуема и требует больших затрат машинного времени. Сокращение размерности модели за счет исключения второстепенных, экономически и статистически несущественных факторов способствует простоте и качеству ее реализации. В то же время построение модели регрессии малой размерности может привести к тому, что такая модель будет недостаточно адекватна исследуемым явлениям и процессам.

Проблема отбора факторных признаков для построения моделей взаимосвязи может быть решена на основе интуитивно-логических или многомерных математико-статистических методов анализа.

Наиболее приемлемым способом отбора факторных признаков является шаговая регрессия (шаговый регрессионный анализ). Сущность метода шаговой регрессии заключается в реализации алгоритмов последовательного "включения", "исключения" или "включения-исключения" факторов в уравнение регрессии и последующей проверке их статистической значимости.

Наличие мультиколлинеарности между признаками вызывает:

искажению величины параметров модели, которые имеют тенденцию к завышению, чем осложняется процесс определения наиболее существенных факторных признаков;

изменению смысла экономической интерпретации коэффициентов регрессии.

Существуют финансовые инструменты, которые по-разному реагируют на изменение макроэкономических показателей. Например, доходность акций компаний, выпускающих автомобили, более чувствительна к общему состоянию экономики, а акций ссудосберегательных учреждений - к уровню процентных ставок. Поэтому в ряде случаев более точным может оказаться прогноз доходности актива на основе многофакторной модели, включающей несколько переменных, от которых зависит доходность данного актива. Выше мы представили модель Шарпа, которая является однофакторной. Ее можно превратить в многофакторную, если слагаемое J3trm представить в качестве нескольких слагаемых, каждое из которых является одной из макроэкономических переменных, определяющих доходность актива. Например, если инвестор полагает, что доходность акции зависит от двух составляющих - общего объема выпуска продукции и процентных ставок, то зависимость между ее доходностью и данными индексами примет вид:

Для определения ожидаемой доходности акции модель (3.35) следует использовать в форме:

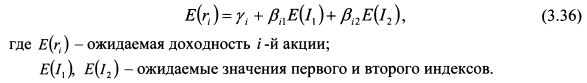
В модели, представленной формулой (3.35), между индексами 1Х и /2 может наблюдаться некоторая корреляция. Данный факт не является помехой для использования ее в форме (3.36) при определении ожидаемой доходности акции. Однако может возникнуть необходимость получить модель (3.35) для случая не коррелируемости индексов. Это позволит, в частности, использовать более простой подход для нахождения эффективной границы портфелей, сократив число вычислений. Рассмотрим прием исключения коррелированности индексов в двухфакторной модели (3.35).

На основе прошлых данных статистики построим регрессию индекса I₂на I₁:

Выделим в уравнении (3.37) величину независимую от I₁. Она представлена случайной переменной 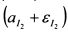. Поэтому, если ее определить как второй индекс в уравнении (3.35), то он будет не коррелирован с индексом I₁. Обозначим новый второй индекс как I'₂. Он равен:

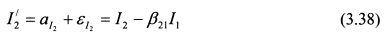Из равенства (3.38) следует, что ожидаемое значение индекса I'₂ равно а_I2. Если необходимо задать новый индекс с нулевым ожидаемым значением, то равенство (3.38) следует уменьшить на величину а_I2:

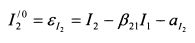
или

Дальнейшее построение модели проведем для последнего случая, т.е. на основе равенства (3.39).

Выразим из равенства (3.39) I₂:

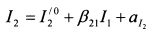
Подставим его значение в (3.35):

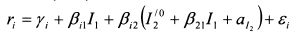
ИЛИ

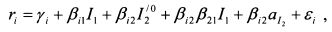
ИЛИ

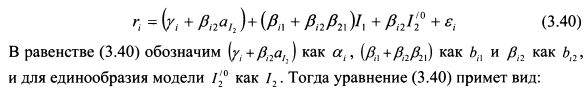
В модели (3.41) индекс I₁- это прежний индекс выпуска продукции, индекс I₂ представляет собой индекс разности между фактическими процентными ставками и ожидаемыми процентными ставками при данном ожидаемом значении индекса выпуска продукции I₁. Соответственно коэффициент b_i2 показывает степень реакции доходности акции к данному индексу. Его также можно определить как степень чувствительности доходности акции к изменению процентных ставок при фиксированном значении индекса выпуска продукции.

Уравнение (3.41) позволяет упростить процесс определения ковариаций активов. Поскольку индексы не коррелированы между собой, не коррелированы значения si и е} как между собой, так и с индексами, то ковариация i-го и j-го активов равна:

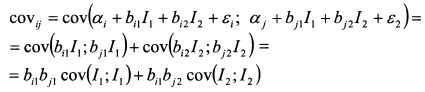
или

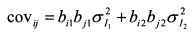
Соответственно риск актива как сумма независимых случайных величин составляет:

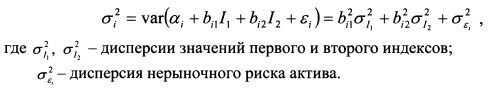
Примеры решения задач.