Охлаждение полого шара с тепловой емкостью внутри

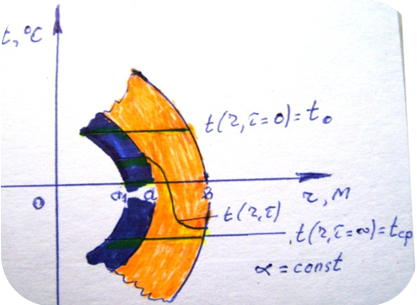Полый шар внутреннего радиусаr = a, м. и наружного r = b, м. с постоянными теплофизическими свойствами материала от начальной одинаковой по координате температуры t₀,⁰Cохлаждается (или нагревается, что в математическом плане одно и то же) при постоянных во времени и координате температуре среды t_ср,⁰С и коэффициенте теплоотдачи (теплообмена)α, Вт/(м.²·⁰С). Внутри шара, в полости может находиться присоединенная высокотеплопроводная тепловая емкость - пусть оболочка наружного радиуса r= a, м. и внутреннего r= a₁, м. На единицу площади внутренней поверхности шара присоединенная тепловая емкость (поверхностная тепловая емкость) тогда составляет

Рис.1. Охлаждение полого шара.

С₀ = 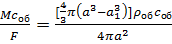, 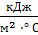…(1) где

M=W 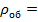[ 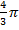( 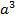– –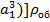масса оболочки, кг. (W –её объем, м³, – эквивалентныйудельный вес её материала, кг/м³);

F = 4 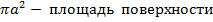контакта тепловой емкости с внутренней поверхностьюполого шара,м²;

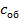–эквивалентная удельная теплоемкость материала оболочки, кДж/(кг·⁰С).

Дифференциальное уравнение теплопроводности в сферической системе координат для одномерного случая,температура зависит только от времени и радиуса и не зависит от углов широтыψ⁰ и долготыϕ⁰, [1,2]

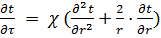,...(2)

где

t = t(r,τ) –температура на координатеr, м в момент времени τ, час; χ =λ / cρ- коэффициенттемпературопроводности материала, м²/час (λ – коэффициент теплопроводности, Вт/(м·⁰С);с – удельная теплоемкость, Вт· час/(кг·⁰С); ρ – плотность материала, кг/м³ ), (1Вт =1Дж/сек, 1Вт·час = 3,6 кДж, 1кДж ≈ 0,278 Вт· час).

Начальное условие

t (r,τ = 0) = t₀.… (3)

Граничные условия внутри и снаружи полого шара

q_{r= a} = - λ 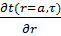= С₀ ,…(4)

q_r=b = -λ 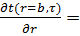α[ t(r=b,τ) – t_ср].…(5)

(В (5) используется гипотеза,закон Ньютона – удельный тепловой поток, тепловой поток через единицу площади поверхности,Вт/м², прямо пропорционален разности температур поверхности и среды, ⁰Сприα – коэффициенте пропорциональности, коэффициенте теплоотдачи, Вт/(м²·⁰С); это, т. наз. граничные условия третьего рода).

При введении безразмерных координат и температур:ρ =(r – a)/(b – a),[ 0…1]иθ =(t(r,τ) –t_ср)/(t₀ –t_ср), [ 1…0 ]; [ r = a + ρ(b – a),t(r,τ) = t_ср + θ(t₀–t_ср)]уравнение (2) получает вид

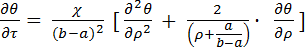,…(6)

а подстановка в уравнение (6)

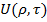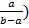=(ρ + ·θ 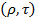…(7)приводит егок уравнению сходному с уравнением теплопроводности для пластины толщиной (b – a)

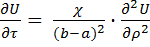. …(8)

Начальное условие (3) для (6,8)тогда получает вид

Θ(ρ,τ=0) = 1,U(ρ,τ=0) = (ρ + 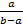) –линейно растет от 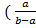)до(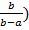, …(9)

а граничные условия (4,5) записываются,как 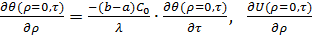- 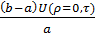= 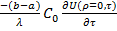,…(10)

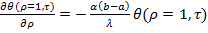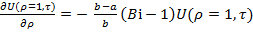, ,…(11)

гдеBi = критерий Био, критерий интенсивности внешнего (числитель) и внутреннего (знаменатель) теплообмена.

Уравнение (8) решается обычно методом Фурье, методом разделения переменных

U(ρ, τ) = U₁(ρ)·U₂(τ)…(12)

и тогда в обычных (не частных) производных получается система двух уравнений

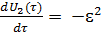= ,т. е. 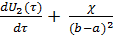U₂(τ) ɛ²= 0.…(13)

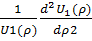= - ɛ², т.е. 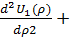U₁(ρ)ɛ² = 0.…(14) Разумеется,ɛне зависит ни от координаты ρ ни от времени τ, 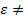ɛ(ρ,τ).

Решения уравнений давно известны [3,4]:

U₁(ρ) = C_2··sinρɛ + C₃ · cosρɛ = (sinρɛ + 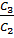cosρɛ)C_2, …(15)

U₂(τ) = C₁exp(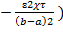 = С₁exp(- ɛ²·F₀), …(16)

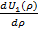( =(cosρɛ - 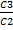sinρɛ)C₂ɛ, 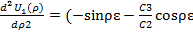)C₂ 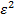, 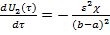U₂(τ)),

где

F₀ = χτ/(b– a)²- критерий безразмерного времени, критерий Фурье; С₁, С₂, С ₃, - взаимосвязанные постоянные,зависящие от ɛ,определяемые изначального и граничных условий (9,10,11).

Таким образом, решение (12)в соответствии с (15,16) имеет вид

U(ρ,τ) = U₁(ρ)U₂(τ) = (sinρɛ + 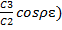C₁C₂exp(-ɛ^2·Fo), …(17)

Θ(ρ,τ) = U(ρ,τ)/ (ρ + 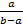). …(18)

Очевидно, что

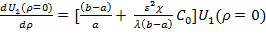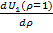, = - (Bi – 1)U₁(ρ=1) и тогда из граничных условий внутри полого шара, ρ =0 и снаружи, ρ = 1 (10,11) с учетом (12)

и решений (15,16) оказывается,что

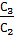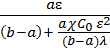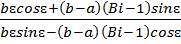= = .…(19)

Из (19) получается трансцендентное уравнение для определенияɛ

ctgɛ = 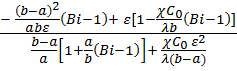,…(20) затем из (19) отношения .

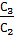При каждых значениях a, b, Bi, С₀ , и при С₀ 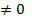χ, λсуществует бесконечное множество решений:ɛ₁<ɛ₂<ɛ₃… (корней).Уравнение решается либо графическим путем и/или подбором: нахождением абсцисс точек пересечения кривых левой и правой частей уравнения, кривых котангенсоид в левой части уравнения и,например,при отсутствии тепловой емкости внутри,С₀=0суммыгиперболы с отрицательным знаком с прямой в правой, что иллюстрируется на рисунке 2 ниже. Корни уравнения положительны и отрицательны (по абсолютной величине равные),кратных корней нет, мнимые корни не отвечают решению. Отрицательные корни в данной задаче не интересны. Положительные корни лежат в каждом из интервалов прохождения котангенсоидот (0, ),….

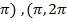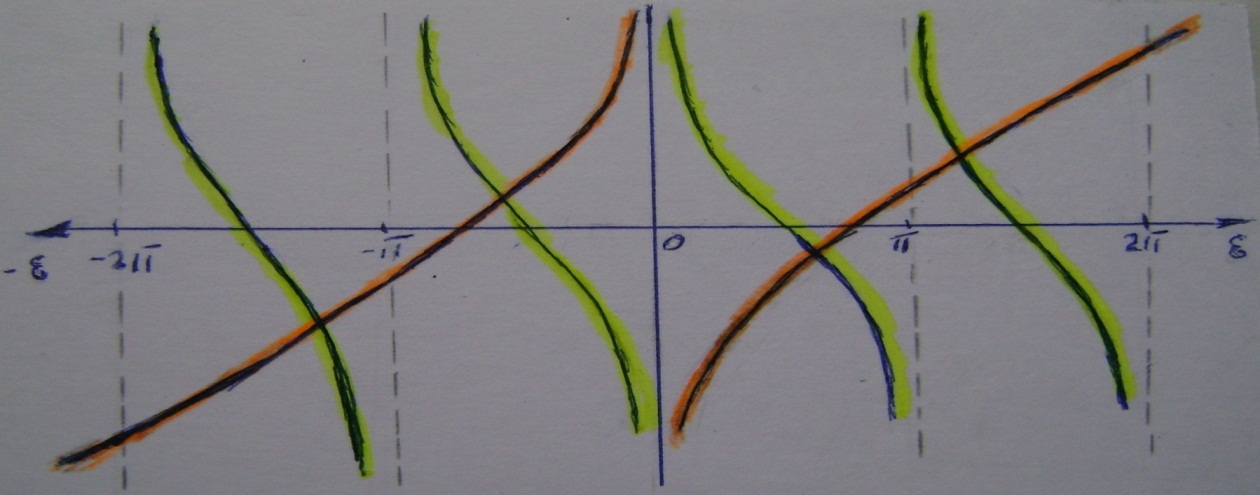
Рис 2. Пример графического представления решения уравнения (20).

Каждому найденному значения корня ɛ_nсоответствует свое частное решение,свое распределение температуры. Общее решение представляется суммой бесконечного ряда

U(ρ,τ) = 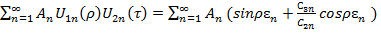exp(- τ),… (21)

где

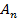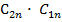= ;U_1n(ρ) = (sinρ 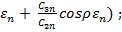С_3n/C_2n = aɛ_n/ [ (b – a) + ;

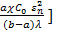Θ(ρ,τ) = 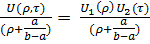,θ(ρ,τ =0) =1,θ(ρ,τ= 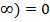.…(22)

Постоянные A_nв уравнении (21) находятся из начального условия, тогда из (21,22)

[ρ + a /(b – a)] = 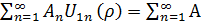_n(sinρ 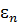+ 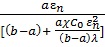cos ),…(23)

что есть разложение в ряд Фурье с заданными параметрамиɛ_n,определяемыми характеристическим уравнением (20).

Для нахождения А_nметодом Фурье следует умножить уравнение (23) на U_1m(ρ) и проинтегрировать от ρ=0до ρ =1,нопредварительно надопоказать, что функции U_1n(ρ) и U_1m(ρ), (n,m = 1,2,3, …) взаимно ортогональны,т. е.

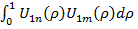= 0при n =mи 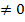при n =m. …(24)Минуя тригонометрические представления в уравнениях (13,14),что малоэффективно, это доказывается тем,чтодля U_1n(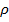)иU_1m(ρ)

d²U_1n(ρ)/dρ² + 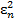U_1n(ρ) = 0, d²U_1m(ρ)/dρ² + 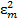U_1m(ρ) = 0,…(25)

при умножении первогоуравнения в (25) на U_1m(ρ),а второго на U_1n(ρ)и вычитания их друг из друга, затем интегрирования по частям результата в промежутке от ρ = 0 до ρ = 1с учетом граничных условий (10,11), это действительно оказываетсятак, еслиn 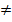m.Тогда из (23) следует, что

А _n = 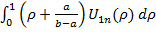: 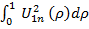. …(26)

После интегрированиячислителя (26) по частям с учетом граничных условий, опуская ввиду громоздкости промежуточные подробности, оказывается, что

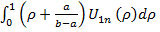= …(27)

(U_1n (ρ =1) =(sin 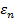+ 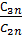cos 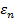),U_1n(ρ=0) = ).

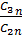Таким образом,интегрированиепо частям умноженного на 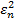знаменателя (26), дает

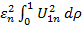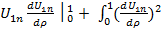= - dρ,…(28)

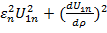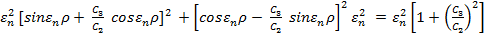= , апосле интегрирования

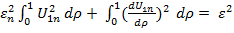[1 + (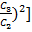.…(29)

При сложении (28), (29) оказывается,что

2 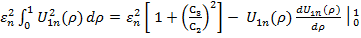.…(30)

Таким образом, при данных граничных условиях

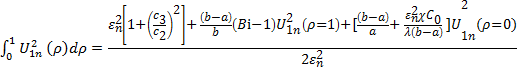. …(31) Тогда из (26,27,31) после преобразований

A_n= ,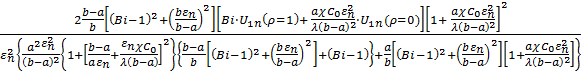

…(32)

исоответственно

Θ(ρ,τ) = 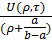= 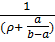· 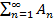U_1n(ρ)·ехр(- ,…(33)

где

;

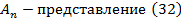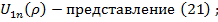
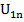(ρ=1), 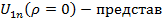ления (27);

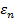- находятся из решения трансцендентного уравнения (20).

Если нет тепловой емкости внутри 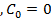; то решение (33) обращается в решение, приведенное в монографии Г.Карслоу и Д. Егера[1] (существенно упрощаетсяв алгебраическом смысле), а при ρ =0 (сплошной шар) – в ещё более простое решение, приводимое в учебной литературе, например,[2].

При значениях критерия безразмерного времени, критерия ФурьеFo = 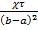>(1/3 -1/2) при охлаждении (нагреве) наступает т. наз. регулярный(упорядоченный)тепловой режим[1,2], и в решении (33) с достаточной степенью точности можно ограничиться одним первым членом ряда, оно получает вид

Θ(ρ,τ) = 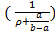A₁ (sinɛ₁ρ + ,…(34)

где

А_1- определяется из (32)при значении первого корня ɛ₁и не зависит от координаты ρ и времени τ, зависит только от a, bи интенсивности внешнего и внутреннего теплообмена – критерия Bi = αb/λ, величины присоединенной внутри тепловой емкости С₀;

m = 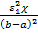- темп охлаждения (нагрева),час^-1,он для всех координат одинаков.

(Уже при втором значении корня ɛ₂, лежащем в области (π -2π), что показано на рис.2 выше, при Fo=1/3exp(-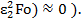

После логарифмирования (34)

lnθ(ρ,τ) = ln 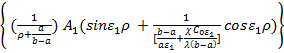- mτ, …(35) в полулогарифмической анаморфозедекартовой системы координат x –y (x=τ, y =lnθ(ρ,τ)) это есть не что иное,как уравнение прямой.

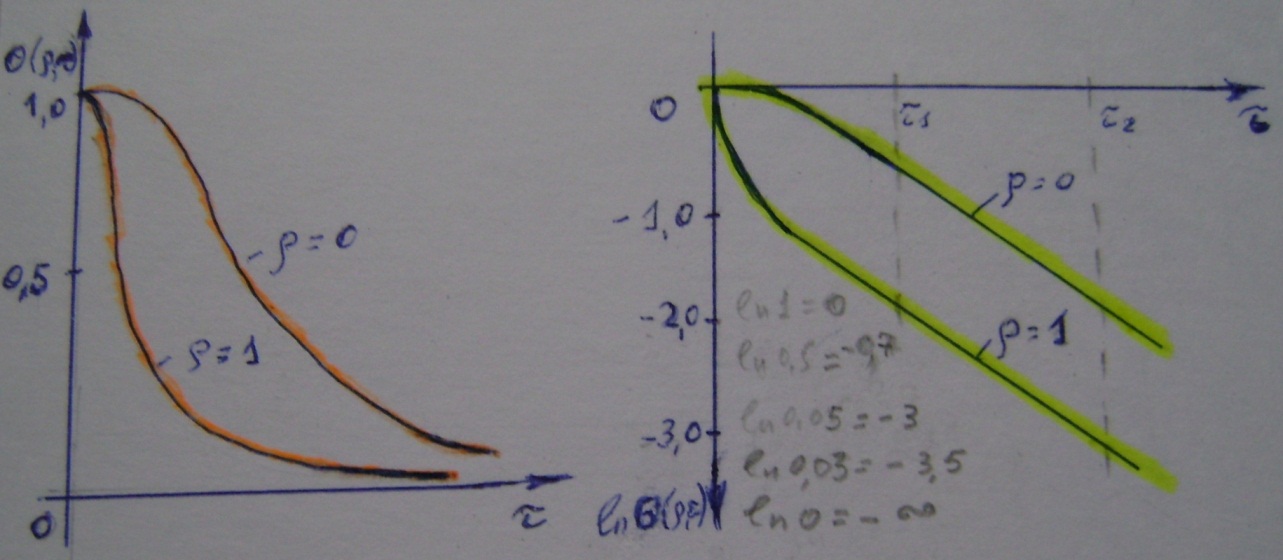
Рис.3. Иллюстрация наступления т. наз. регулярного теплового режима.

Из (35) следует, что темп охлаждения (нагрева)

m = 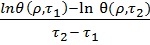,[час ^-1], …(36)

а при найденном значенииm находится при необходимостииз (32) А₁,при n=1.

Таким образом, найдя mи A₁из эксперимента, если он проводится, не стоит его продолжать, дальнейшее уже известно из (34). Кроме того- точность эксперимента с уменьшением разностей температур падает.

Время тепловой инерции – время, необходимое для достижения наиболее инерционной точкой охлаждаемого (нагреваемого) объекта, обычно внутри, ρ=0, температуры среды со степенью недостижимости- (3 -5)%, (теоретически 0% -достижим только при τ 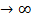), согласно (35),

τ_ин = 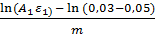....(37)

Этим далеко не ограничиваются решения в форме уравнений регулярного теплового режима. Например 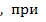регулярном тепловом режиме 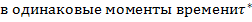отношение температур в различных точках конструкции неизменно. Так, если внутри полого шара нет тепловой ёмкости, то

Θ(ρ=1,τ= 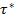)/θ(ρ=0,τ= 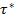) = (1- - ) 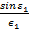+ cosɛ_1, ...(38)

т. е. по отношению температур в одни и те же моменты времени на координатах ρ =1 и ρ=0 можно найти первый корень ɛ₁, а по нему из соотношения (34)для m= 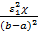и коэффициент температуропроводности.

* * *

Если граничные условия, воздействия переменны во времени, например, переменная температура окружающей среды (суточные колебания), то решения находятся с использованием интегрального уравнения типа свертки (теорема Дюамеля) [1,7]

q=q^ɪ·F_нач. + q^ɪ* F^r, … (39)

где

q^ɪ- решение при единичном воздействии Fº1;

q - решение при воздействии F=F(t);

r - символ производной по времени;

_* - символ свертки: j_*y =j(t)_*y(t)= 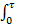j(t-w)y(w)dw=y_*j.

При аналитически простых воздействиях решение (39) может быть найдено аналитическим путем, при сложных воздействиях - численным интегрированием по программе TEZIS (температурные задачи, интегралы свертки) [7]. При численном интегрировании по формуле прямоугольников на равномерной временной сетке (39) получает вид

q(t_i) = 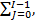q^ɪ(t_i-t_j)× F(t_j+1-t_j),(i, j - 0,1,2,3, …). … (40)).

Эта программа решает и обратные задачи теплопроводности (восстановление F или q^ɪ).

Данные задачи труднорешаемы, но решаемы с применением специальных алгоритмов.

* * * * * *

Исаак Ньютон (1641 г. р.) считал, что ” примеры не менее поучительны, чем правила”,(разумеется, минуя исключения). Пример.

Полый малотеплопроводный (неметаллический) шар,например, из органического стекла, эбонита или эпоксидной смолы внутреннего радиуса 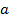= 0,1м и наружного b =0,2м от начальной нормальной температуры t₀=20⁰C охлаждается при температуре средыt_ср = - 40⁰C и коэффициенте теплоотдачи α ≈10 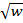= 10 Вт/(м² · ⁰С) – (w – скорость ветра, легкий ветерок ≈1м/сек,слегка колышет серебристый блеск волны…,слегка колышет листья деревьев). Объем шара W = (4/3) π(b³ –a³)= 0,0293м³, площадь наружной поверхности 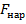= =4πb²≈0,5м^2., внутренней - 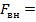4π 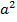≈0,126 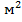.).Теплофизические свойства материала шара:плотность ρ 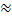1100кг/м³, тогда вес Wρ ≈32кг (в старой русской системе мер - два пуда), коэффициент теплопроводности λ 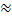0,2 Вт/(м· ⁰С), удельная теплоемкость с 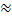1.5кДж/(кг·⁰С) = =0,4 Втчас/(кг·⁰С) [4,5], т.е. коэффициент температуропроводностиχ 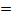λ/(cρ) ≈≈0,45·10^-3м²/час.Критерий теплообмена, критерий БиоBi =αb/λ ≈10.

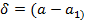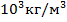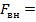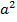Внутри шара может быть присоединенная тепловая емкость, например, в виде алюминиевой оболочки толщиной ≈ 6мм. Плотность алюминия ρ = 2,7· , удельная теплоемкость - с = 1кДж/(кг·⁰С) [4,5]. Тогда вес оболочки -≈1,9кг., величина присоединенной тепловой емкости на единицу площади контакта 4π - С₀ 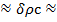15кДж/ (м²·⁰С).(Сплошной алюминиевый шар внутри весил бы 11,3кг, а присоединенная теплоемкость составила бы – 95кДж/(м^2· · ⁰С)).

Регулярный тепловой режим охлаждения настанет при значении критерия Фурье Fo= χτ/(b-a)²> (1/3 -1/2), т. е. через τ > (7 - 10) час.

Из (20) при данных a,b, Biи без присоединенной тепловой емкости внутри шара, С₀=0 корни уравнения ₁ = 1.73, ɛ₂ = 4.2, …, а из (29) постоянные A_{1 =}1,06, А₂ =- 0.063 ….

При значении критерия ФурьеFo =1/3 безразмерные температуры на внутренней и наружной поверхностях шара тогда составят:

Θ(ρ=0,Fo=1/3) = A₁U₁(ρ=0)exp(-ɛ₁²Fo) + A₂ U₂(ρ=0)exp(-ɛ₂²Fo) + … ≈

≈ A₁ɛ₁ exp(- ɛ₁²Fo) +A₂ɛ₂exp(- ɛ₂²Fo) + … ≈ 1,06·1,73·exp(-1) – 0, 063·4,2·exp(-5)+ … ≈ ≈ 1,94/e - 0,25/e⁵ + … ≈ 0,67;

Θ(ρ=1, Fo=1/3) = A₁·(sinɛ ₁ + 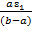cosɛ₁)/( 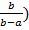·[exp(-1)] + … = 1,06·0,36exp(-1) – 0,063·(- 1,47)exp(-5) +…≈ 0,38/e + 0,07/e⁵≈0,38/e +0,07/e⁵+ … ≈ 0,14. В градусах стоградусной шкалы температур (обычно ей приравнивают и градусы Цельсия ≈ ⁰Ц) это ≈0⁰С и ≈ -30⁰С.

Время тепловой инерции шара,времяпрактически необходимое для достижения им температуры среды, согласно (37)

τ_ин= 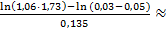(26 – 30)часов, т.е. немного больше суток.

Отношение безразмерных температур θ(ρ=1,Fo=1/3)/θ(ρ=0,Fo=1/3) =0,14/0,67 = =0,206, что дает из трансцендентного уравнения (38) то же значение первого корня ɛ₁ = 1,73.

Цитируемая литература.

1. Г. Карслоу и Д. Егер. Теплопроводность твердых тел. М., ῎Наука“, 1964.

2. В. П. Исаченко, В. А. Осипова, А. С. Сукомел. Теплопередача.М.-Л., “Энергия῎,1965.

3. В. И. Смирнов. Курс высшей математики, Т 2. М., Госиздат Ф-МЛ, 1961.

4. Г. Корн и Т. Корн. Справочник по математике. М., ῎Наука“, 1970.

5. В. Ф. Чиркин. Теплофизические свойства материалов. М., Физматгиз, 1959.

6. Г. Н. Иванов. Тепловые свойства веществ. М., ЦНИИатоминформ, 1997.

7. Ю.К. Семенов. Взрывчатые вещества. Том 1, Глава 9. Учебное пособие / под общей ред. Р. И. Илькаева /. Саров, РФЯЦ – ВНИИЭФ,2001.

Date: 2015-07-17; view: 711; Нарушение авторских прав