Сжато-изгибаемые элементы

Сжато-изгибаемыми элементами называются такие, на которые действует изгибающий момент и централь­но приложенное продольное сжимающее усилие. Изги­бающий момент может создаваться: а) внецентренно приложенной сжимающей силой и тогда элемент назы­вают внецентренно сжатым или б) поперечной нагруз­кой. При расчете сжато-изгибаемых деревянных стерж­ней применяют теорию краевых напряжений, предложен­ную проф. д-ром техн. наук К. С. Завриевым. В соответст­вии с этой теорией несущая способность стержня счита­ется исчерпанной в тот момент, когда краевое напряжение сжатию делается равным расчетному сопротивлению.

Эта теория менее точная, чем теория устойчивости, однако она дает более простое решение и поэтому при­нята в действующих нормах проектирования СНиП П-25-80.

Так как жесткость стержня не является бесконечной, то он под влиянием изгибающего момента прогибается.

При этом центрально приложенная сжимающая сила теперь уже будет иметь эксцентриситет, равный дефор­мации стержня от момента, и таким образом создаст дополнительный момент (рис. II 1.8). Появление допол­нительного момента от нормальной силы увеличит де­формацию стержня, что приведет к еще большему воз­растанию дополнительного момента. Такое наращивание дополнительного момента и прогибов будет некоторое время продолжаться, но затем затухнет.

Полный прогиб стержня и уравнение кривой неизве­стно, поэтому непосредственно по формуле краевых на­пряжений нельзя найти эти напряжения:

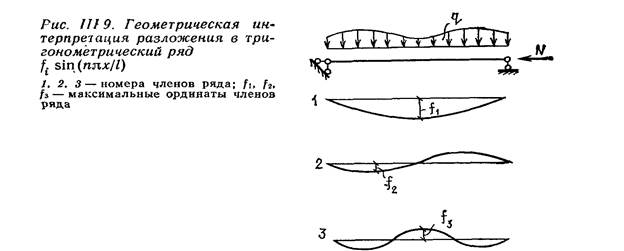
Так как в двух написанных уравнениях есть три неиз­вестных Ос, у, М_х, то следует найти еще одно уравнение. Всякую кривую можно аналитически выразить в виде ряда, который при этом должен быть быстро сходящим­ся и удовлетворять краевым значениям. Таким является тригонометрический ряд

Геометрическая интерпретация ряда показана на рис. Ш.9. Как видно, /v есть максимальная ордината кривой каждого члена ряда.

При симметричной нагрузке первый член ряда дает точность, равную 95—97 %. Для упрощения решения бу­дем считать нагрузку симметричной. Тогда можно огра­ничиться только первым членом ряда.

Однако третье уравнение принесло четвертое неизвест­ное fi. Поэтому вспомним строительную механику, где было показано, что вторая производная у" уравнения кривой деформирования равна изгибающему моменту, деленному на жесткость с обратным знаком, т. е.

d *yldx* = — MJEJ. (Ill. 30)

Тогда после дифференцирования уравнения кривой по­лучим

Приравняв значения (Ш.31) и (Ш.ЗО) получим

Теперь значение М_х из (III.32) и у из (111.29) под­ставим в выражение (111.28) и после преобразования, имея в виду, что n²EJ/l²=N_KP, a sin (я*//) при х=//2, где при симметричной нагрузке будет находиться мак­симальная ордината прогиба y_max=/i, равен единице, получим, что

Найденная зависимость позволяет решить вопрос об определении напряжений. Для этого /значение /i=#max из (Ш.ЗЗ) надо подставить в выражение (111.27):

с_с = NIF + M_qIW + NM_q/(N_KP — N)W. (III. 34)

Date: 2015-06-11; view: 574; Нарушение авторских прав